Образование поверхности и каркасные методы решения задач. Построить две проекции конической поверхности ψ (S, k), заданной проекциями определителя.
Построить две проекции конической поверхности ψ (S, k), заданной проекциями определителя. а) построить каркас поверхности, из ее прямолинейных образующих li; б) по одной проекции линии m, лежащей на поверхности, найти ее вторую проекцию.
КОМПЛЕКСНАЯ ГРАФИЧЕСКАЯ РАБОТА № 3 Образование поверхности и каркасные методы решения задач Условия задач КГР-4 В соответствии с заданным вариантом на листе чертёжной бумаги формата А3 (297х420) с помощью чертёжных инструментов решить две задачи: Задача 1. Построить две проекции поверхности, заданной проекциями определителя. Задача 2. Построить недостающую проекцию линии, лежащей на поверхности. Общие указания к выполнению 1. Исходные данные задания перечертить, располагая исходные проекции в направлении длинной стороны чертёжного листа примерно в том же масштабе, что и на примере выполнения. 2. Кривые линии, заданные на исходном чертеже, следует вычерчивать с помощью лекал с примерным соблюдением их формы и кривизны. 3. Очерк поверхности вращения (ПВ) получают в плоскости главного меридиана с помощью некоторого множества параллелей ПВ, которые получают вращением ряда точек образующей l около оси i (вар.1-10). 4. При построении недостающей проекции линии АВ, лежащей на ПВ, прибегают к помощи, например, семейства параллелей. 5. Для построения очерка ПВ с наклонной осью (вар. 9) следует применять метод вписанных сфер. Пример использования вписанной сферы для построения очерковых образующих a и b конуса вращения с наклонной осью на плоскости π3 показан на рис. 4. Множество вписанных сфер позволяют построить криволинейные очерковые образующие. Рис. 4 Рис. 5 6. В случае линейчатых поверхностей, каркас которых состоит из прямых линий (вар. 13-16, 19-23), следует строить очерковую-огибающую – кривую, касательную последовательному множеству образующих (рис. 5). 7. Толщина линий чертежа должна соответствовать ГОСТ 2.303-68: – толщину сплошных основных – линий очерка, направляющих линий – принять равной ≈ 0,5 мм; – толщину сплошных тонких – образующих и линий связи принять равной ≈ 0,2 мм; 8. Для начертаний следует использовать остро отточенные карандаши с графитами повышенной твёрдости марки Т, 2Т, 3Т или F, 2F. Основные вспомогательные линии построения необходимо сохранить! Примечания. На консультациях (СРСП) обязательно иметь при себе: а) чертёж (семестровую работу) в процессе выполнения; б) карточку с вариантом задания, условия задания и общие указания к их выполнению; в) чертёжные инструменты.
Срок выдачи задания – 10 неделя Срок сдачи задания – 12 неделя
Варианты задания 1–28 (для студентов и учащихся колледжа) Варианты 1 – 5 Построить две проекции поверхности вращения (ПВ) α;, заданной проекциями определителя: а) по одной проекции линии АВ, лежащей на поверхности, найти ее вторую проекцию; б) построить очерк поверхности вращения и дать ей название.
Вариант 6,7,8 Построить две проекции поверхности вращения β. По одной проекции линии а построить её вторую проекцию.
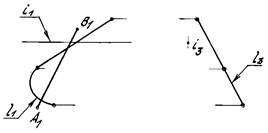
Вариант 9 Построить две проекции поверхности вращения α {(i, l)[ l – построить очерк поверхности вращения и дать ей название. Вариант 10 Построить две проекции сферы φ; (О, С), где О – центр, С – точка на поверхности сферы, заданной определителем. По одной проекции линии т
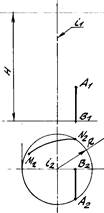
Построить две проекции прямого закрытого геликоида φ; с базовой гелисой (винтовой линией) левого хода, радиуса R и шага Н. а) построить каркас поверхности из последовательных положений образующей АВ; б) по одной проекции линии МN, лежащей на поверхности, найти ее вторую проекцию. Вариант 12. Построить две проекции прямого открытого геликоида φ; с базовой гелисой (винтовой линией) левого хода, радиуса R и шага Н. а) построить каркас поверхности из последовательных положений образующей АВ; б) по одной проекции линии МN, лежащей на поверхности, найти ее вторую проекцию.
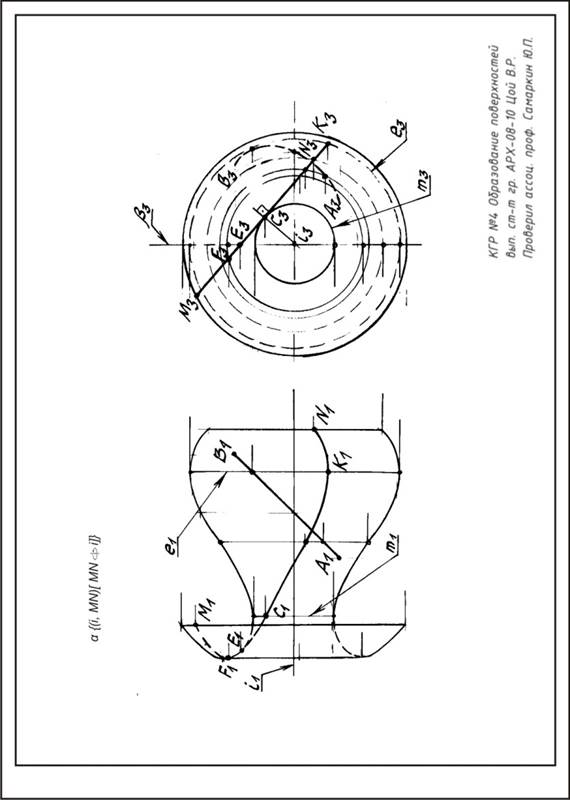
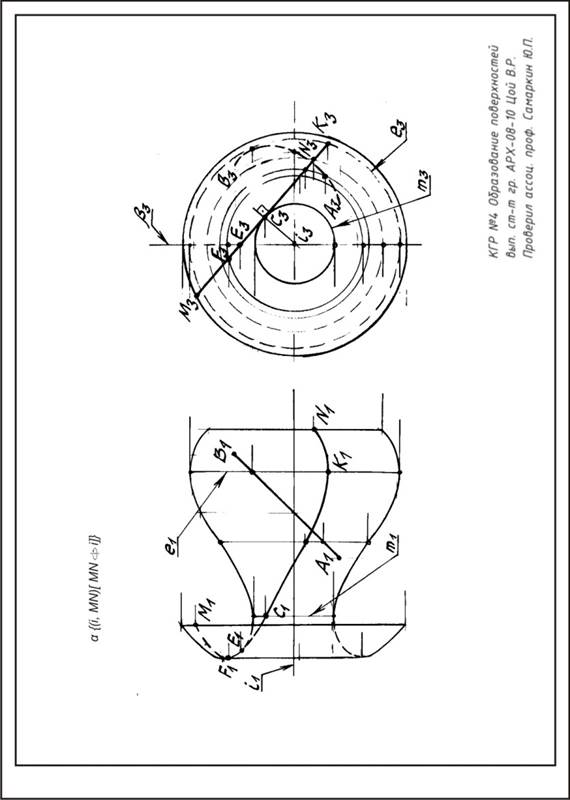
Построить две проекции косого закрытого геликоида β с базовой гелисой (винтовой линией) левого хода, радиуса R и шага Н. а) построить каркас поверхности из последовательных положений образующей АВ, а также её огибающую; б) по одной проекции линии МN, лежащей на поверхности, найти ее вторую проекцию.
Вариант 16. Построить две проекции косого открытого геликоида β с базовой гелисой (винтовой линией) левого хода, радиуса R и шага Н. а) построить каркас поверхности из последовательных положений образующей АВ, а также её огибающую; б) по одной проекции линии МN, лежащей на поверхности, найти ее вторую проекцию.
Варианты 17-18 Построить две проекции поверхности торса β; заданной проекциями определителя в виде ребра возврата v: β {(v)[АВi v]} а) построить каркас поверхности, состоящий из образующих АВi; точка К – точка касания образующей АВ к ребру возврата v, при этом В1 К1=2А1 К1 б) по одной проекции линии MN, лежащей на поверхности, найти ее вторую проекцию. Фронтальные проекции образующих АВi брать одинаковыми и равными величине n=R или 1,5R.
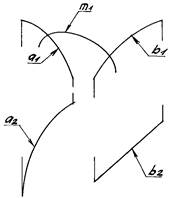
Построить две проекции линейчатой поверхности (ЛП) с тремя направляющими, заданной проекциями определителя φ (a, b, с). а) построить каркас поверхности, состоящий из ее прямолинейных образующих li; б) по одной проекции линии m, лежащей на поверхности, найти ее вторую проекцию.
Построить каркас из двух семейств образующих косой плоскости α, заданной пространственным четырехугольником АВСD. а) по одной проекции линии MN, лежащей на поверхности, найти ее вторую проекцию; б) определить положение направляющих плоскостей (плоскостей параллелизма) для каждого из двух семейств образующих.
Вариант 22 Построить две проекции поверхности коноида ψ, заданного проекциями определителя: ψ {(m(CЕ),n(АВ), π1)[li а) построить каркас поверхности, состоящий из ее прямолинейных образующих li; б) по одной проекции линии ЕК, лежащей на поверхности, найти ее вторую проекцию.
Варианты 23-24 Построить две проекции поверхности φ; с плоскостью параллелизма, заданной проекциями определителя. а) построить каркас поверхности, из ее прямолинейных образующих li; б) по одной проекции линии m, лежащей на поверхности, найти ее вторую проекцию.
Построить две проекции конуса вращения ω(SО, R), где O – центр окружности n основания заданного радиуса R=1/3 SO, расположенной во фронтально-проектирующей плоскости α. а) построить каркас поверхности из ее прямолинейных образующих li; б) по одной проекции линии m, лежащей на поверхности, найти ее вторую проекцию.
Вариант 26 Построить две проекции цилиндра вращения ω(i,ОО′, R), где O – центр окружности n основания заданного радиуса R=1/3 ОO′, расположенной в профильно-проектирующей плоскости β;. а) построить каркас поверхности из ее прямолинейных образующих li; б) по одной проекции линии m, лежащей на поверхности, найти ее вторую проекцию.
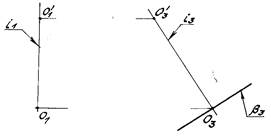
Вариант 27 Построить две проекции цилиндрической поверхности ψ (l, k) заданной проекциями определителя. а) построить каркас поверхности, из ее прямолинейных образующих li; б) по одной проекции линии MN, лежащей на поверхности, найти ее вторую проекцию. Вариант 28 Построить две проекции конической поверхности ψ (S, k), заданной проекциями определителя. а) построить каркас поверхности, из ее прямолинейных образующих li; б) по одной проекции линии m, лежащей на поверхности, найти ее вторую проекцию.
|






 i]}
i]}
 i]}
i]}


 i]}
i]}

 i]}
i]}

 построить её вторую проекцию.
построить её вторую проекцию.

 i]}
i]}



 i]}
i]}



 li
li  ]}
]}
 li
li  li II π1}.
li II π1}.


 a,li b, li II π1]}
a,li b, li II π1]}

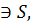 li
li  ]}
]}