Линейная зависимость и независимость векторов
и ее усовершенствованный вариант
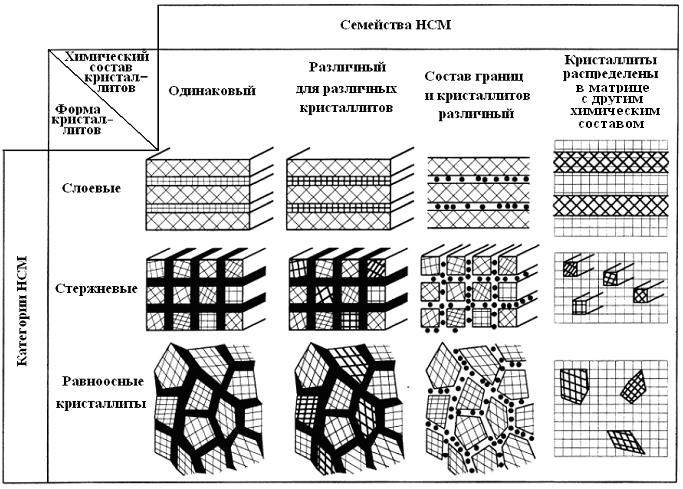
Глейтер предложил классификацию наноструктурированных материалов (НСМ), основываясь на двух группах параметров: химическом составе кристаллитов и размерности (форме) кристаллитов (рис.1.4) [15]. Форма кристаллитов представлена тремя типами: слоевая, стержневая (с толщиной слоя или диаметром стержня порядка нескольких нанометров) и одинаковоориентированными кристаллитами. В зависимости от химического состава кристаллитов три группы НСМ сгруппированы в четыре семейства. Всего получилось 12 категорий кристаллических НСМ. В самом простом случае (первое семейство на рис. 1.4) все кристаллиты и межкристаллитные области имеют один и тот же состав. Во втором семействе кристаллиты имеют разный химический состав (на рис. 1.4 использованы различные толщины линий для различения этих кристаллитов). Квантовые ямы и мультислоевые структуры соответствуют этому случаю. Если состав кристаллитов отличен от состава границ, то получается третье семейство НСМ. Если один тип атомов (молекул) локализуется на границах, то образуются локальные химические модуляции структуры. Такие материалы известны: так, например, в кристаллах W на границах зерен сегрегируется Ga [15]. Недавно получен материал, структура которого состоит из наноразмерных кристаллов Al2O3, разделенных сетью некристаллических слоев Ga [16]. Четвертое семейство НСМ образовано наноразмерными кристаллитами, распределенными в матрице с другим химическим составом. Примером является Ni3Al в матрице Ni [15]. Первое семейство НСМ является однофазным, а остальные — многофазными материалами. Интересно отметить, что нанотубулярным формам вещества не нашлось места в этой классификации.
Рис. 1.4. Классификация наноструктурированных кристаллических материалов по-Глейтеру [15]. Границы кристаллитов в первом и во втором семействах наноструктурированных материалов выделены черным цветом, чтобы подчеркнуть различие в расположении атомов на границах и в кристаллитах. Химический состав кристаллитов и границ в первом семействе одинаков. Во втором семействе границы различают кристаллиты двух типов, отличающихся химическим составом.
МИКРОСТРУКТУРА. 1) Зернистое строение металла, сплава, минерала, крупного кристалла. Размеры зерен обычно 10–6-10–2 мм, углы их разориен-тации составляют несколько градусов. Микроструктура выявляется с помо-щью микроскопа (оптического или электронного), позволяющего опреде-лить форму, ориентировку, а иногда фазовый состав зерен (кристаллитов). 2) Субкристаллитное (масштаба 1-1000 Å) строение вещества, отражающее его реальную структуру или идеальную структуру. Изучается с помощью электронной микроскопии высокого разрешения или дифракционными ме-тодами.
Линейная зависимость и независимость векторов Определение 1. Множество элементов произвольной природы называется векторным пространством или линейным векторным пространством, если для этих элементов введены операции сложения и умножения на действительное число, причем для этих операций справедливы 8 свойств, указанных для операций с геометрическими векторами. Пусть заданы векторы называется линейной комбинацией заданных векторов Определение 1. Система векторов Если не выполнены условия определения 1, то система векторов называется линейно зависимой системой векторов. Система векторов линейно зависима тогда и только тогда, когда один из векторов системы равен линейной комбинации остальных векторов этой системы. Геометрическими векторы называются коллинеарными векторами, если они параллельны одной прямой. Геометрическими векторы называются компланарными векторами, если они параллельны одной плоскости. Теорема 1. Любые 2 не коллинеарных вектора на плоскости линейно независимы, причем любой третий вектор является их линейной комбинацией. Теорема 2. Любые 3 не компланарных вектора на плоскости линейно независимы, причем любой четвертый вектор является их линейной комбинацией. Доказательство теорем 1 и 2 проводится в школьном курсе и приведено на лекции. Определение 2. Линейно независимая система векторов линейного векторного пространства Следовательно, любые 2 не коллинеарных вектора Аналогично любые 3 не компланарных вектора Заметим, что в рассмотренных примерах число векторов базиса не зависит от выбора базиса. Это число называется размерностью векторного пространства. Плоскость является линейным пространством размерности 2, а обычное пространство имеет размерность 3.
|

 ,
,  ,…,
,…,  векторного пространства и числа
векторного пространства и числа  ,
, 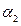 ,…,
,…,  . Величина
. Величина  (1)
(1)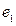 ,
,  ,…,
,…, 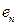 . При этом числа
. При этом числа 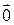 (нулевому вектору), если все коэффициенты линейной комбинации равны 0. Может ли линейная комбинация векторов быть равной 0 при других обстоятельствах?
(нулевому вектору), если все коэффициенты линейной комбинации равны 0. Может ли линейная комбинация векторов быть равной 0 при других обстоятельствах? и
и 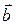 на плоскости образуют базис. Это означает, что для произвольного вектора
на плоскости образуют базис. Это означает, что для произвольного вектора  существуют числа
существуют числа  и
и 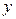 такие, что
такие, что  . Числа
. Числа  существуют числа
существуют числа  такие, что
такие, что 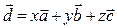 . Числа
. Числа  и
и  . Их разность дает соотношение
. Их разность дает соотношение  . Однако векторы базиса
. Однако векторы базиса  ,
, 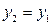 ,
,  . Следовательно, 2 написанных разложения являются одним и тем же разложением вектора по базису.
. Следовательно, 2 написанных разложения являются одним и тем же разложением вектора по базису.


