В векторном пространстве (пока для нас это плоскость или обычное пространство) базис можно выбрать различными способами. Базис с соответствующими координатами называют системой координат. Какая система координат является самой лучшей? На самом деле, ответ на этот вопрос не является простым. В разных ситуациях применяются различные системы координат.
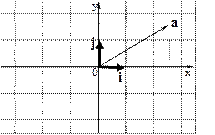
В школе мы познакомились с декартовой системой координат. Суть ее состоит в том, что в качестве базиса берутся взаимно перпендикулярные векторы единичной длины. Например, на плоскости это 2 взаимно перпендикулярных вектора  , ,  . .
| 
|
Произвольный вектор  представляется в виде
представляется в виде 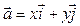 . Координаты геометрических векторов на плоскости являются проекциями конца вектора, приставленного к началу координат, на оси координат. А как правильно расположить векторы
. Координаты геометрических векторов на плоскости являются проекциями конца вектора, приставленного к началу координат, на оси координат. А как правильно расположить векторы  ,
,  ? Что такое ориентация системы координат? На приведенном рисунке движение в ближайшем направлении от вектора
? Что такое ориентация системы координат? На приведенном рисунке движение в ближайшем направлении от вектора  к вектору
к вектору  происходит против часовой стрелки. Такая пара векторов называется правой парой векторов на плоскости. Если векторы
происходит против часовой стрелки. Такая пара векторов называется правой парой векторов на плоскости. Если векторы  и
и  поменять местами, получится левая пара векторов.
поменять местами, получится левая пара векторов.
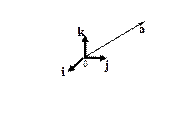
Рассмотрим теперь 3 взаимно перпендикулярных вектора  , ,  , ,  единичной длины в пространстве. Здесь произвольный вектор единичной длины в пространстве. Здесь произвольный вектор  представляется в виде представляется в виде  . .
| 
|
Координаты этого вектора являются проекциями вектора  на оси, порожденные базисными векторами
на оси, порожденные базисными векторами  ,
,  ,
,  .
.
Теперь посмотрим, как правильно расположить векторы  ,
,  ,
,  . На приведенном рисунке движение в ближайшем направлении от вектора
. На приведенном рисунке движение в ближайшем направлении от вектора  к вектору
к вектору  , наблюдаемое с конца вектора
, наблюдаемое с конца вектора  , происходит против часовой стрелки. Такая тройка векторов называется правой тройкой векторов в пространстве. Если какие-то 2 вектора поменять местами, то получится левая тройка векторов.
, происходит против часовой стрелки. Такая тройка векторов называется правой тройкой векторов в пространстве. Если какие-то 2 вектора поменять местами, то получится левая тройка векторов.

 ,
,  .
.

 представляется в виде
представляется в виде 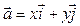 . Координаты геометрических векторов на плоскости являются проекциями конца вектора, приставленного к началу координат, на оси координат. А как правильно расположить векторы
. Координаты геометрических векторов на плоскости являются проекциями конца вектора, приставленного к началу координат, на оси координат. А как правильно расположить векторы  единичной длины в пространстве. Здесь произвольный вектор
единичной длины в пространстве. Здесь произвольный вектор  .
.




