Смешанное произведение векторов. Определение 2. Смешанным произведением упорядоченной тройки геометрических векторов , , называется число
Определение 2. Смешанным произведением упорядоченной тройки геометрических векторов Итак, для того, чтобы найти смешанное произведение векторов, надо, не меняя порядок этих векторов, найти их векторное произведение, а затем скалярное произведение полученного и оставшегося векторов. Для смешанного произведения векторов используются обозначения: Теорема 3. Смешанное произведение упорядоченной тройки некомпланарных векторов Доказательство. Пусть заданы векторы
Рассмотрим теперь скалярное произведение векторов Итак, результатом смешанного произведения векторов является число, равное 0, если векторы 5. Вычисление смешанного произведения Теорема 4. Смешанное произведение упорядоченной тройки некомпланарных векторов равно определителю, у которого первая строка состоит из координат первого вектора, вторая строка состоит из координат второго вектора, третья строка состоит из координат третьего вектора. Доказательство. Пусть заданы векторы Отметим некоторые свойства смешанного произведения. 1) Если поменять местами 2 вектора тройки векторов, их смешанное произведения изменит знак. 2) Объем параллелепипеда равен модулю смешанного произведения векторов, образующих этот параллелепипед. 3) Объем тетраэдра равен одной шестой модуля смешанного произведения векторов, образующих этот тетраэдр. 4) Смешанное произведение трех векторов равно 0 тогда и только тогда, когда эти векторы линейно зависимы.
|

 ,
,  ,
,  называется число, равное
называется число, равное  .
. .
. ,
,  и
и  равно объему параллелепипеда, построенного на этих векторах, и взятому со знаком «
равно объему параллелепипеда, построенного на этих векторах, и взятому со знаком « », если тройка векторов – правая, и взятому со знаком «
», если тройка векторов – правая, и взятому со знаком « », если тройка векторов – левая.
», если тройка векторов – левая. и
и  . Это вектор, перпендикулярный плоскости векторов
. Это вектор, перпендикулярный плоскости векторов 
 и
и  , т. е. смешанное
, т. е. смешанное 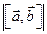 (параллелограмма, построенного на векторах
(параллелограмма, построенного на векторах  к этому основанию. Теорема доказана.
к этому основанию. Теорема доказана. . Если мы этот вектор скалярно умножим на вектор
. Если мы этот вектор скалярно умножим на вектор  , то получим искомую величину
, то получим искомую величину  . Теорема доказана.
. Теорема доказана.


