Векторное произведение векторов. 2. Реакции средних циклов практически такие же, как и для ациклических алканов.
1. Реакции малых циклов:
2. Реакции средних циклов практически такие же, как и для ациклических алканов.
Окисление:
Отдельные представители циклоалканов – см. учебник.
ЛИТЕРАТУРА: 1. Белобородов В.Л., Зурабян С.Э., Лузин А.П., Тюкавкина Н.А. – Органическая химия (основной курс) – Дрофа, М., 2003 г., с. 157 – 182.
19.09.08
Векторное произведение векторов Определение 1. Векторным произведением геометрических векторов Для векторного произведения могут быть использованы следующие обозначения: Справедливы следующие свойства векторного произведения: 1) 3) Свойства 1), 3) и 4) прямо следуют из определения векторного произведения. Свойство 2) мы принимаем без доказательства. Еще раз подчеркнем, что результатом векторного произведения векторов является вектор, по длине равный площади параллелограмма, построенного на векторах 3. Вычисление вектор ного произведения в ДСК Теорема 2. В декартовой системе координат векторное произведение геометрических пространственных векторов Доказательство. Рассмотрим векторное произведение векторов
Для получения заключительного результата заметим, что в силу свойства 4 векторные произведения равных векторов равны нулевому вектору, т. е. Полученный результат можно записать в виде
|



 и
и  называется вектор
называется вектор  , такой что: а)
, такой что: а) 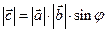 ; б)
; б) 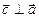 ,
,  ; в) векторы
; в) векторы  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  .
. и
и  равно вектору
равно вектору  .
. . Используя свойства 2), 3) векторного произведения векторов, запишем следующие преобразования:
. Используя свойства 2), 3) векторного произведения векторов, запишем следующие преобразования: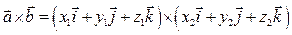

 .
. ,
,  ,
,  . Кроме того, из правой ориентации базисных векторов
. Кроме того, из правой ориентации базисных векторов  ,
,  ,
, 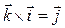 ,
,  ,
,  ,
, 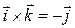 . Продолжая вычисления, получим, что
. Продолжая вычисления, получим, что  . Теорема доказана.
. Теорема доказана. . Здесь определитель мы понимаем, как формальное разложение по своей первой строке. Иными словами, данную формулу можно описать следующим образом. В декартовой системе координат векторное произведение геометрических пространственных векторов
. Здесь определитель мы понимаем, как формальное разложение по своей первой строке. Иными словами, данную формулу можно описать следующим образом. В декартовой системе координат векторное произведение геометрических пространственных векторов 


