Решето Аткина.

Алгоритмы формирования таблиц простых чисел

 

Описание алгоритма:

Алгоритм состоит из следующих шагов.

1. Выписываются все натуральные числа из диапазона от 1 до n.

 

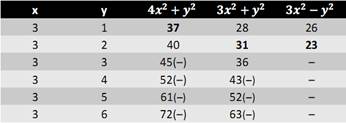
2. Перебираются все возможные пары чисел x, y, где x<=sqrt(n) и y<=sqrt(n). Т.е. (1,1), (1,2),…, (1,sqrt(n)), (2,1), (2,2),…, (sqrt(n),sqrt(n)).

3. Для каждой пары чисел вычисляются значения следующих трех уравнений:

a) 4*x^2+y^2;

b) 3*x^2+y^2;

c) 3*x^2-y^2, значение вычисляется только при x>y.

4. Для каждого вычисленного значения уравнений вычисляются остатки от деления на 12, причем

a) если остаток равен 1 или 5 для значения первого уравнения;

b) если остаток равен 7 для значения второго уравнения;

с) если остаток равен 11 для значения третьего уравнения.

То в исходном ряду чисел от 1 до n число помечается как простое.

Замечание: если какое-то число Z присутствует в значениях нескольких уравнений (допустим a и b), и остаток от деления на 12 этого числа удовлетворяет условиям обоих групп, то число помечается два раза: сначала как простое, а потом как составное.

5. На последнем этапе проверяется кратность помеченных чисел квадратам простых чисел из диапазона от 5 до sqrt(n). Если число кратно квадрату, то оно помечается как составное.

Пример работы алгоритма для n = 40.

1. Выписываем все натуральные числа из диапазона от 1 до 40.

2. Перебираются все возможные пары чисел от (1,1) до (6,6) (Т.к. sqrt(40) ~ 6).

2. Вычисляем значения уравнений для каждой пары чисел x и y.

 

 

 

4. Вычисляем остаток от деления на 12 и помечаем простые числа.

5. Проверяем кратность помеченных чисел квадратам простых из диапазона от 5 до 6.

5 — простое число, 6 — составное, значит проверяем на кратность 5^2=25 помеченные числа. В результате 25 — нужно вычеркнуть. В итоге остаются только простые числа от 1 до 40.

 

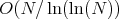Алгоритм имеет асимптотическую сложность и требует бит памяти. На входных значениях порядка 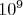решето Аткина быстрее решета Эрастофена в 9.2 раза. Приведу график роста превосходства алгоритма Аткина на числах от 2 до :

В результате можно наблюдать следующую скорость выполнения:

10 000 000	0.15 сек.
100 000 000	2.16 сек.
1 000 000 000	48.76 сек.