Векторы и их свойства
Векторы и их свойства Контрольные вопросы: 1. Определение вектора. 2. Разложение вектора по базису. 3. Длина вектора. Направляющие косинусы. 4. Проекция вектора на заданное направление.
1. Вектором называется направленный отрезок. Расстояние между началом и концом вектора называется его длиной (или модулем) и обозначается Вектор, длина которого равна нулю, называется нулевым вектором и обозначается Вектор, длина которого равна единице, называется единичным вектором. Единичный вектор, направление которого совпадает с направлением вектора Два ненулевых вектора называются противоположными, если они имеют одинаковую длину и противоположно направлены. Два вектора называются коллинеарными, если они лежат на одной или параллельных прямых. Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Два коллинеарных вектора 2. Разложение вектора по базису. Если Коэффициенты x, y, z линейной комбинации называются координатами вектора Пусть система векторов 3. Длина вектора
Пусть вектор
Направляющие косинусы связаны соотношением Пусть даны два вектора 1) векторы 2) векторы
При сложении векторов их соответствующие координаты складываются, при вычитании – вычитаются, при умножении вектора на число – соответственно умножаются на это число:
4. Проекция вектора на заданное направление. Проекцией вектора
Рис.1 Точки А1, В1 – это точки пересечения оси и с перпендикулярными ей плоскостями, проходящими через точки А и В. Нахождение проекции вектора
|

 или
или  .
. .
. , называется ортом вектора
, называется ортом вектора 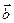 называются равными, если они сонаправлены и имеют равные длины.
называются равными, если они сонаправлены и имеют равные длины. - орты координатных осей прямоугольной системы координат Oxyz, то любой вектор
- орты координатных осей прямоугольной системы координат Oxyz, то любой вектор  .
. ,
, 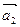 ,
,  является базисом, вектор
является базисом, вектор  – их линейная комбинация. Разложение любого вектора в базисе, если оно существует, является единственным. Значит,
– их линейная комбинация. Разложение любого вектора в базисе, если оно существует, является единственным. Значит, определяется по формуле:
определяется по формуле: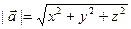 .
. образует с координатными осями Ox, Oy, Oz углы α, β, γ соответственно. Направление вектора
образует с координатными осями Ox, Oy, Oz углы α, β, γ соответственно. Направление вектора  ,
, 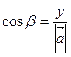 ,
, 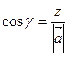 .
. .
. и
и  . Тогда:
. Тогда: .
. ,
, .
. на ось и называется число, равное длине вектора
на ось и называется число, равное длине вектора  (рис.1), взятой со знаком «плюс», если направление вектора
(рис.1), взятой со знаком «плюс», если направление вектора 
 на направление, заданное вектором
на направление, заданное вектором  ,может осуществляться по формуле, если
,может осуществляться по формуле, если 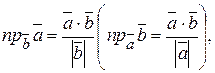 т.е.
т.е.  .
.


