1. Даны два вектора 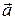 ={3; -1; 5} и
={3; -1; 5} и 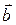 ={1; 2; -3}. Найти вектор
={1; 2; -3}. Найти вектор 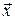 , если
, если 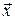 ^О z,
^О z, 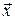 ^
^ 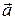 ,
, 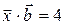 .
.
2. Даны векторы 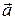 ={3; 2; 1},
={3; 2; 1}, 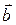 ={2; -3; 0}. Найти вектор
={2; -3; 0}. Найти вектор 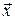 , если
, если 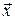 ^
^ 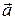 ,
,  ^
^  ,
, 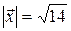 .
.
3. Даны векторы 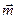 ={0; 2;1},
={0; 2;1}, 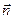 ={1; 0; 2},
={1; 0; 2},  ={1; 1; 1}. Найти вектор
={1; 1; 1}. Найти вектор  , если
, если  ^
^ 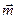 ,
,  ^
^ 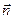 ,
,  ×
×  =3.
=3.
4. Вектор  , перпендикулярный к
, перпендикулярный к  ={3; 2; 2} и
={3; 2; 2} и  ={18; -22; 5}, образует с осью О у тупой угол. Найти его координаты, зная, что
={18; -22; 5}, образует с осью О у тупой угол. Найти его координаты, зная, что 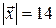 .
.
5. Найти вектор  , зная, что он перпендикулярен к
, зная, что он перпендикулярен к  ={2; –3; 1} и
={2; –3; 1} и  ={1, –2, 3} и удовлетворяет условию
={1, –2, 3} и удовлетворяет условию  · {1; 2; –7} = 10.
· {1; 2; –7} = 10.
6. Вектор  , перпендикулярен к оси О z и вектору
, перпендикулярен к оси О z и вектору  ={8; –15; 3}, образует с осью О x острый угол, |
={8; –15; 3}, образует с осью О x острый угол, |  | = 51. Найти вектор
| = 51. Найти вектор  .
.
7. Найти вектор 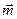 , зная, что
, зная, что 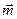 ^О z,
^О z, 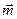 ^
^  , |
, | 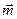 | = |
| = |  |, где
|, где  ={–5; 3; –4}.
={–5; 3; –4}.
8. Найти вектор  , зная, что
, зная, что  ^
^  ,
,  ^
^  ,
, 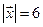 , где
, где  = {2; –3; –1},
= {2; –3; –1},  ={1; 6; –2}.
={1; 6; –2}.
9. Найти вектор  , зная, что
, зная, что  ^О,
^О,  ^
^  ,
,  ×
×  = 4, где
= 4, где  ={2; –1; 1},
={2; –1; 1},  ={1; 1; –1}.
={1; 1; –1}.
10. Найти вектор 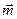 , зная, что |
, зная, что | 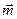 | = 52,
| = 52, 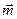 ^О x,
^О x, 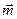 ^
^  и
и 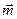 образует острый угол с осью О y.
образует острый угол с осью О y.  = {7; –12; 5}.
= {7; –12; 5}.
11. Найти вектор `х, зная, что он перпендикулярен к векторам  ={0; 2; 1},
={0; 2; 1},  ={1; 0; 2}, образует с осью О y тупой угол и
={1; 0; 2}, образует с осью О y тупой угол и 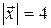 .
.
12. Найти вектор  , если известно, что
, если известно, что  ^
^  ,
,  ^
^  ,
, 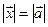 ,
, 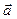 ={2; –1; 1},
={2; –1; 1},  ={1; 1; –1}.
={1; 1; –1}.
13. Найти вектор  , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам  ={2; 3; 1} и
={2; 3; 1} и  ={1; –2;3} и удовлетворяет условию
={1; –2;3} и удовлетворяет условию  ×{2; –1; 1} = –6.
×{2; –1; 1} = –6.
14. Найти вектор  , перпендикулярен к векторам
, перпендикулярен к векторам  ={4; –2; –3} и
={4; –2; –3} и  ={0; 1; 3} и образующий с осью О y тупой угол,
={0; 1; 3} и образующий с осью О y тупой угол, 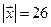 .
.
15. Найти вектор  , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам  ={4; –6; 2},
={4; –6; 2},  ={1; –2; 3} и удовлетворяет условию
={1; –2; 3} и удовлетворяет условию 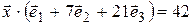 .
.
16. Найти вектор  , зная, что
, зная, что  ^О x,
^О x,  ^
^  ,
,  ×
×  =2, где
=2, где  ={6; 3; 1},
={6; 3; 1},  ={1; 1; 1}.
={1; 1; 1}.
17. Найти вектор  , зная, что
, зная, что  ^
^  ,
,  ^
^  ,
, 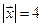 , если
, если  ={2; –1; 1},
={2; –1; 1},  ={0; 3;1}.
={0; 3;1}.
18. Найти вектор 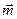 , зная, что он перпендикулярен к
, зная, что он перпендикулярен к  ={2; 3; –1} и
={2; 3; –1} и  ={1; –2; 3} и удовлетворяет условию
={1; –2; 3} и удовлетворяет условию 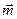 ×{ 1; 1; 1} = –18.
×{ 1; 1; 1} = –18.
19. Вектор  перпендикулярный к оси О z и вектору
перпендикулярный к оси О z и вектору  ={8; –15; 3}, образует острый угол с осью О x. Найти
={8; –15; 3}, образует острый угол с осью О x. Найти  , если
, если 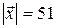 .
.
20. Найти вектор  , перпендикулярный к векторам
, перпендикулярный к векторам  ={2; 3; –1} и
={2; 3; –1} и  ={1; –2; 3} и удовлетворяющий условию
={1; –2; 3} и удовлетворяющий условию  ×
× 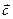 =12, где
=12, где 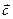 ={2; –1; 1}.
={2; –1; 1}.
21. Найти вектор 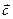 , если известно, что
, если известно, что 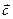 ^
^  ,
, 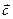 ^
^  , |
, | 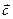 |=1, где
|=1, где  ={5; 7; 1},
={5; 7; 1},  ={4; 2; –1}.
={4; 2; –1}.
22. Найти вектор 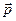 , зная, что
, зная, что 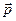 ^О y,
^О y, 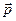 ^
^  ,
, 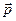 ×
×  =–3, где
=–3, где  ={2; 3; –1},
={2; 3; –1},  ={1; 1; 1}.
={1; 1; 1}.
23. Даны два вектора  ={2;–4; 3} и
={2;–4; 3} и  ={–2; 3; 1}. Найти вектор
={–2; 3; 1}. Найти вектор  , если
, если  ^О z,
^О z,  ^
^  ,
,  ×
×  =6.
=6.
24. Найти вектор  , зная, что
, зная, что  ^
^  ,
,  ^
^  ,
, 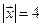 , где
, где  ={3; –2;1},
={3; –2;1},  ={4; 6; –1}.
={4; 6; –1}.
25. Даны два вектора  ={1; 3; –5} и
={1; 3; –5} и  ={–2; 1; 2}. Найти вектор `с, зная, что он перпендикулярен векторам
={–2; 1; 2}. Найти вектор `с, зная, что он перпендикулярен векторам  и
и  и удовлетворяет условию
и удовлетворяет условию 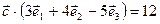 .
.
26. Найти вектор 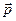 , зная, что он перпендикулярен к
, зная, что он перпендикулярен к  ={2; –1; 3} и
={2; –1; 3} и  ={3; –2; 1}, образует с осью О x острый угол, |
={3; –2; 1}, образует с осью О x острый угол, | 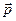 |=16.
|=16.
27. Найти вектор  , зная, что
, зная, что  ^О z,
^О z,  ^
^  ,
, 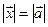 , где
, где  ={–3; 5; 4}.
={–3; 5; 4}.
28. Даны векторы  ={0; 2; 1},
={0; 2; 1},  ={1; 0; 2},
={1; 0; 2}, 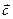 ={1; 1; 1}. Найти вектор
={1; 1; 1}. Найти вектор  , если
, если  ^
^  ,
,  ^
^  ,
,  ×
× 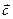 =3.
=3.
29. Найти вектор 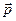 , зная, что он перпендикулярен к векторам
, зная, что он перпендикулярен к векторам 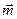 ={2; –1; 0} и
={2; –1; 0} и 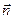 ={2; –2; 1}, образует с осью О y тупой угол и |
={2; –2; 1}, образует с осью О y тупой угол и | 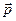 |=5.
|=5.
30. Найти вектор  , зная, что
, зная, что  ^
^  ,
,  ^
^  ,
,  ×{1; 1; 1}=–18, где
×{1; 1; 1}=–18, где  ={2; –3; 1},
={2; –3; 1},  ={–2; 1;1}.
={–2; 1;1}.

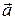 ={3; -1; 5} и
={3; -1; 5} и 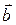 ={1; 2; -3}. Найти вектор
={1; 2; -3}. Найти вектор 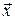 , если
, если 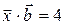 .
. ^
^  ,
, 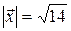 .
.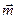 ={0; 2;1},
={0; 2;1}, 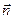 ={1; 0; 2},
={1; 0; 2},  ={1; 1; 1}. Найти вектор
={1; 1; 1}. Найти вектор  ={3; 2; 2} и
={3; 2; 2} и 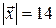 .
.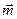 , зная, что
, зная, что  ,
, 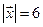 , где
, где 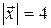 .
.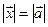 ,
, 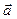 ={2; –1; 1},
={2; –1; 1}, 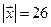 .
.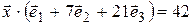 .
.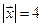 , если
, если 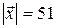 .
.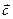 =12, где
=12, где 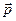 , зная, что
, зная, что 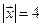 , где
, где 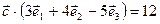 .
.


