1. Даны вершины четырехугольника А (1; –2; 2), В (1; 4; 0), С (–4; 1; 1), Д (–5;–5;3). Доказать, что его диагонали АС и ВД взаимно перпендикулярны.
2. Проверить, что векторы 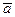 ={7; 6; –6} и
={7; 6; –6} и  ={6; 2; 9} могут быть взяты за ребра куба. Найти третье ребро.
={6; 2; 9} могут быть взяты за ребра куба. Найти третье ребро.
3. Дан треугольник АВС с вершинами в точках А (3; 5; 4), В (5; 8; 3), С (1; 9; 9). Найти длину высоты, опущенной из вершины С.
4. Точки А (1; 2) и С (3; 6) – противоположные вершины квадрата. Найти координаты двух других его вершин.
5. Зная векторы  ={1; 2; –1} и
={1; 2; –1} и  = {2; 0; –4}, совпадающие с двумя сторонами треугольника, найти угол при вершине А и площадь треугольника.
= {2; 0; –4}, совпадающие с двумя сторонами треугольника, найти угол при вершине А и площадь треугольника.
6. Доказать, что векторы  и
и  , где А (3; 6; –2), В (6; –2; 3) могут быть взяты за ребра кеба. Найти конец С третьего ребра.
, где А (3; 6; –2), В (6; –2; 3) могут быть взяты за ребра кеба. Найти конец С третьего ребра.
7. Даны вершины четырехугольника А (1; 2; 3), В (7; 3; 2), С (–3; 0; 6) и Д (9; 2; 4). Доказать, что его диагонали взаимно перпендикулярны.
8. Даны вершины треугольника А (4; 1; 0), В (2; 2; 1) и С (6; 3; 1). Найти длину высоты опущенной из вершины В.
9. Проверить, что векторы 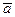 ={12; –3; –3} и
={12; –3; –3} и  ={4; 5; 11} могут быть взяты за ребра куба. Найти третье ребро.
={4; 5; 11} могут быть взяты за ребра куба. Найти третье ребро.
10. Зная векторы  ={2; –2; –3} и
={2; –2; –3} и  ={2; 2; 9}, совпадающие с двумя сторонами треугольника, найти угол при вершине С и площадь треугольника.
={2; 2; 9}, совпадающие с двумя сторонами треугольника, найти угол при вершине С и площадь треугольника.
11. Даны три последовательные вершины параллелограмма: А (–3; –2; 0), В (3; –3; 1) и С (5; 0; 2). Найти его четвертую вершину и угол между диагоналями АС и ВД.
12. Проверить, что точки А (3; –1; 2), В (1; 2; –1), С (–1; 1; –3), Д (3; –5; 3) служат вершинами трапеции. Найти длины ее параллельных сторон.
13. Зная векторы  ={2; –2; 1} и
={2; –2; 1} и  ={–4; 1; –3}, совпадающие с двумя сторонами треугольника, найти угол при вершине А и высоту ВD.
={–4; 1; –3}, совпадающие с двумя сторонами треугольника, найти угол при вершине А и высоту ВD.
14. Доказать, что четырехугольник с вершинами А (2; 1; –4), В (1; 3; 5), С(7; 2; 3), D (8; 0; –6) есть параллелограмм. Найти длины его сторон.
15. Даны три последовательные вершины параллелограмма: А (1; 1; 4), В (2; 3; –1), С (–2; –2; 0). Найти его четвертую вершину и угол между диагоналями.
16. Проверить, что векторы 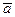 =
=  ,
,  =
=  могут быть взяты за ребра куба. Найти третье ребро.
могут быть взяты за ребра куба. Найти третье ребро.
17. Зная векторы  =
=  ,
,  =
=  , совпадающие со сторонами треугольника, найти угол при вершине А площадь треугольника.
, совпадающие со сторонами треугольника, найти угол при вершине А площадь треугольника.
18. Дан треугольник АВС с вершинам в точках А (–1;–2;4), B (–4;–2;0) и С (3;–2;1). Найти длину высоты, опущенной из вершины С.
19. Даны вершины четырехугольника А (1;–2; 2), В (1; 4; 0), С (–4; 1; 1), D (–5;–5; 3). Доказать, что его диагонали АС и ВD взаимно перпендикулярны.
20. Даны 3 последовательные вершины параллелограмма А (1;–2;3), В (3; 2; 1), С (6; 4; 4). Найти его четвертую вершину и угол между диагоналями.
21. Зная векторы  =
=  ,
,  =
=  , совпадающие с двумя сторонами треугольника, найти угол при вершине А и высоту ВD.
, совпадающие с двумя сторонами треугольника, найти угол при вершине А и высоту ВD.
22. Доказать, что векторы 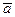 =
= 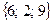 ,
,  =
=  могут быть взяты за ребра куба. Найти третье ребро.
могут быть взяты за ребра куба. Найти третье ребро.
23. Дан треугольник АВС с вершинами в точках А (3; 2; –3), В (5; 1; –1), С(1; –2; 1). Найти внутренние углы этого треугольника.
24. Даны вершины четырехугольника А (7; 3; 2), В(–3; 0; 6), С (9; 2; 4), D (1; 2; 3). Доказать, что его диагонали взаимно перпендикулярны.
25. Проверить, что точки А (3; –1; 2), В (1; 2; –1), С (–1; 1; –3), D (3; –5; 3) служат вершинами трапеции. Найти длины ее параллельных сторон.
26. Векторы  =
=  и
и  =
=  совпадают с двумя сторонами треугольника.Найти высоту, опущенную из вершины С.
совпадают с двумя сторонами треугольника.Найти высоту, опущенную из вершины С.
27. Доказать, что векторы  =
=  и
и  =
=  могут быть взяты за ребра куба. Найти третье ребро.
могут быть взяты за ребра куба. Найти третье ребро.
28. Даны вершины треугольника А (4; 1; 0), В (2; 2; 1) и С (6; 3; 1). Найти длину высоты, опущенной из вершины А.
29. Даны три последовательные вершины параллелограмма А (–3; –2; 0), В (3; –3; 1), С (5; 0; 2). Найти его четвертую вершину и угол между диагоналями.
30. Зная векторы  =
=  и
и  =
=  , совпадающие с двумя сторонами треугольника, найти угол при вершине С и площадь треугольника.
, совпадающие с двумя сторонами треугольника, найти угол при вершине С и площадь треугольника.
Задание 10*
1. Какую работу производит сила  , если точка приложения ее перемещается из положения А(1; –1; 0) в положение В(1; 1; 1)?
, если точка приложения ее перемещается из положения А(1; –1; 0) в положение В(1; 1; 1)?
2. Сила  приложена к точке А(2;1;-1). Определить направляющие косинусы момента этой силы относительно начала координат.
приложена к точке А(2;1;-1). Определить направляющие косинусы момента этой силы относительно начала координат.
3. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(2;-2;-1) в точку В(3;-2;-1)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(2;-2;-1) в точку В(3;-2;-1)?
4. Какую работу совершает сила  при перемещении точки ее приложения из М(2;4;-1) в N(0;1;0)?
при перемещении точки ее приложения из М(2;4;-1) в N(0;1;0)?
5. Сила  приложена к точке А(3;4;5). Определить моменты этой силы относительно точки С(-1;0;-1).
приложена к точке А(3;4;5). Определить моменты этой силы относительно точки С(-1;0;-1).
6. Сила  приложена к точке А(2;-1;1). Определить момент этой силы относительно начала координат.
приложена к точке А(2;-1;1). Определить момент этой силы относительно начала координат.
7. Найти работу, производимую силой  при перемещении точки приложения силы из А(-1;1;1) в В(4;0;1).
при перемещении точки приложения силы из А(-1;1;1) в В(4;0;1).
8. Три силы  ,
,  ,
,  приложены к точке С(2;2;2). Определить величину момента равнодействующей этих сил относительно начала координат.
приложены к точке С(2;2;2). Определить величину момента равнодействующей этих сил относительно начала координат.
9. Определить момент силы  , приложенной к точке А(-1;1;1) относительно точки В(0;3;-2).
, приложенной к точке А(-1;1;1) относительно точки В(0;3;-2).
10. Даны три силы 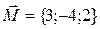 ,
,  ,
,  , приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения перемещается из А(1;2;1) в В(3;4;0).
, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения перемещается из А(1;2;1) в В(3;4;0).
11. Сила  приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
12. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(3;2;-4) в точку В(1;4;-3)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(3;2;-4) в точку В(1;4;-3)?
13. Сила  приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
14. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из точка А(3;2;-4) в точку В(1;4;-3)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из точка А(3;2;-4) в точку В(1;4;-3)?
15. Сила  приложена к точке М(2;-1;3). Определить момент этой силы относительно точки А(-1;3;2).
приложена к точке М(2;-1;3). Определить момент этой силы относительно точки А(-1;3;2).
16. Сила  приложена к точке А(1;-2;1). Определить величину момента этой силы относительно точки В(1;1;1).
приложена к точке А(1;-2;1). Определить величину момента этой силы относительно точки В(1;1;1).
17. Сила  приложена к точке А(3;2;1). Найти момент этой силы относительно точки В(4;-3;7).
приложена к точке А(3;2;1). Найти момент этой силы относительно точки В(4;-3;7).
18. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(2;-3;5) в точку В(-1;2;-4)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(2;-3;5) в точку В(-1;2;-4)?
19. Вычислить работу, которую совершает сила  по перемещению материальной точки из А(1;0;1) в В(2;2;2).
по перемещению материальной точки из А(1;0;1) в В(2;2;2).
20. Сила  приложена к точке М(4;2;-3). Определить момент этой силы относительно точки К(2;4;0).
приложена к точке М(4;2;-3). Определить момент этой силы относительно точки К(2;4;0).
21. Под действием силы 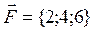 переместилась из А(-1;0;2) в В(3;4;1). Найти работу силы F.
переместилась из А(-1;0;2) в В(3;4;1). Найти работу силы F.
22. Сила  приложена к точке М(4;-2;3). Определить момент этой силы относительно точки А(3;2;-1).
приложена к точке М(4;-2;3). Определить момент этой силы относительно точки А(3;2;-1).
23. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-1;3;2) в точку В(0;2;4).
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-1;3;2) в точку В(0;2;4).
24. Сила  приложена к точке А(4;2;-4). Определить величину момента этой силы относительно начала координат.
приложена к точке А(4;2;-4). Определить величину момента этой силы относительно начала координат.
25. Вычислить работу силы  , если ее точка приложения, двигаясь прямолинейно, перемещается из А(0;0;2) в В(0;2;0).
, если ее точка приложения, двигаясь прямолинейно, перемещается из А(0;0;2) в В(0;2;0).
26. Сила  приложена к точке А(3;4;-3). Определить момент этой силы относительно В(0;1;1).
приложена к точке А(3;4;-3). Определить момент этой силы относительно В(0;1;1).
27. Найти работу, производимую силой 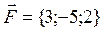 , когда точка ее приложения, двигаясь прямолинейно, перемещается из А(1;1;1) в В(2;-5;-7).
, когда точка ее приложения, двигаясь прямолинейно, перемещается из А(1;1;1) в В(2;-5;-7).
28. Сила  приложена к точке А(4;2;-3). Найти величину момента этой силы относительно точки С(2;4;0).
приложена к точке А(4;2;-3). Найти величину момента этой силы относительно точки С(2;4;0).
29. Какую работу совершает сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-2;1;0) в В(3;2;-1)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-2;1;0) в В(3;2;-1)?
30. Сила  приложена к точке А(1;0;1). Найти момент этой силы относительно точки С(0;0;1).
приложена к точке А(1;0;1). Найти момент этой силы относительно точки С(0;0;1).
Задание 10*
1. Какую работу производит сила  , если точка приложения ее перемещается из положения А (1;-1;0) в положение В(1;1;1)?
, если точка приложения ее перемещается из положения А (1;-1;0) в положение В(1;1;1)?
2. Сила  приложена к точке А(2;1;-1). Определить направляющие косинусы момента этой силы относительно начала координат.
приложена к точке А(2;1;-1). Определить направляющие косинусы момента этой силы относительно начала координат.
3. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(2;-2;-1) в точку В(3;-2;-1)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(2;-2;-1) в точку В(3;-2;-1)?
4. Какую работу совершает сила  при перемещении точки ее приложения из М(2;4;-1) в N(0;1;0)?
при перемещении точки ее приложения из М(2;4;-1) в N(0;1;0)?
5. Сила  приложена к точке А(3;4;5). Определить моменты этой силы относительно точки С(-1;0;-1).
приложена к точке А(3;4;5). Определить моменты этой силы относительно точки С(-1;0;-1).
6. Сила  приложена к точке А(2;-1;1). Определить момент этой силы относительно начала координат.
приложена к точке А(2;-1;1). Определить момент этой силы относительно начала координат.
7. Найти работу, производимую силой  при перемещении точки приложения силы из А(-1;1;1) в В(4;0;1).
при перемещении точки приложения силы из А(-1;1;1) в В(4;0;1).
8. Три силы  ,
,  ,
,  приложены к точке С(2;2;2). Определить величину момента равнодействующей этих сил относительно начала координат.
приложены к точке С(2;2;2). Определить величину момента равнодействующей этих сил относительно начала координат.
9. Определить момент силы  , приложенной к точке А(-1;1;1) относительно точки В(0;3;-2).
, приложенной к точке А(-1;1;1) относительно точки В(0;3;-2).
10. Даны три силы 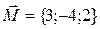 ,
,  ,
,  , приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения перемещается из А(1;2;1) в В(3;4;0).
, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения перемещается из А(1;2;1) в В(3;4;0).
11. Сила  приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
12. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(3;2;-4) в точку В(1;4;-3)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(3;2;-4) в точку В(1;4;-3)?
13. Сила  приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
14. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из точка А(3;2;-4) в точку В(1;4;-3)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из точка А(3;2;-4) в точку В(1;4;-3)?
15. Сила  приложена к точке М(2;-1;3). Определить момент этой силы относительно точки А(-1;3;2).
приложена к точке М(2;-1;3). Определить момент этой силы относительно точки А(-1;3;2).
16. Сила  приложена к точке А(1;-2;1). Определить величину момента этой силы относительно точки В(1;1;1).
приложена к точке А(1;-2;1). Определить величину момента этой силы относительно точки В(1;1;1).
17. Сила  приложена к точке А(3;2;1). Найти момент этой силы относительно точки В(4;-3;7).
приложена к точке А(3;2;1). Найти момент этой силы относительно точки В(4;-3;7).
18. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(2;-3;5) в точку В(-1;2;-4)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(2;-3;5) в точку В(-1;2;-4)?
19. Вычислить работу, которую совершает сила  по перемещению материальной точки из А(1;0;1) в В(2;2;2).
по перемещению материальной точки из А(1;0;1) в В(2;2;2).
20. Сила  приложена к точке М(4;2;-3). Определить момент этой силы относительно точки К(2;4;0).
приложена к точке М(4;2;-3). Определить момент этой силы относительно точки К(2;4;0).
21. Под действием силы 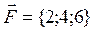 переместилась из А(-1;0;2) в В(3;4;1). Найти работу силы F.
переместилась из А(-1;0;2) в В(3;4;1). Найти работу силы F.
22. Сила  приложена к точке М(4;-2;3). Определить момент этой силы относительно точки А(3;2;-1).
приложена к точке М(4;-2;3). Определить момент этой силы относительно точки А(3;2;-1).
23. Какую работу производит сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-1;3;2) в точку В(0;2;4).
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-1;3;2) в точку В(0;2;4).
24. Сила  приложена к точке А(4;2;-4). Определить величину момента этой силы относительно начала координат.
приложена к точке А(4;2;-4). Определить величину момента этой силы относительно начала координат.
25. Вычислить работу силы  , если ее точка приложения, двигаясь прямолинейно, перемещается из А(0;0;2) в В(0;2;0).
, если ее точка приложения, двигаясь прямолинейно, перемещается из А(0;0;2) в В(0;2;0).
26. Сила  приложена к точке А(3;4;-3). Определить момент этой силы относительно В(0;1;1).
приложена к точке А(3;4;-3). Определить момент этой силы относительно В(0;1;1).
27. Найти работу, производимую силой 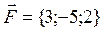 , когда точка ее приложения, двигаясь прямолинейно, перемещается из А(1;1;1) в В(2;-5;-7).
, когда точка ее приложения, двигаясь прямолинейно, перемещается из А(1;1;1) в В(2;-5;-7).
28. Сила  приложена к точке А(4;2;-3). Найти величину момента этой силы относительно точки С(2;4;0).
приложена к точке А(4;2;-3). Найти величину момента этой силы относительно точки С(2;4;0).
29. Какую работу совершает сила  , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-2;1;0) в В(3;2;-1)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-2;1;0) в В(3;2;-1)?
30. Сила  приложена к точке А(1;0;1). Найти момент этой силы относительно точки С(0;0;1).
приложена к точке А(1;0;1). Найти момент этой силы относительно точки С(0;0;1).
Контрольные вопросы
1. Что называется вектором?
2. Какие операции над векторами можно выполнять?
3. Дайте определение координаты вектора.
4. Что называется модулем вектора?
5. Дайте определение направляющим косинусам вектора.
6. Что называется проекцией вектора на ось?
7. Дайте определение скалярного произведения векторов.
8. Сформулируйте свойства скалярного произведения векторов.
9. С помощью каких формул можно вычислить скалярное произведение векторов?
10. Приведите формулы вычисления длины вектора и угла между векторами в координатной форме.
11. Сформулируйте условие ортогональности двух векторов.
12. Дайте определение векторного произведения векторов.
13. Сформулируйте свойства векторного произведения векторов.
14. Сформулируйте условие коллинеарности двух векторов.
15. Коллинеарны ли векторы  и
и  , если коллинеарны векторы
, если коллинеарны векторы  и
и  ?
?
16. Докажите, что векторное произведение не изменится, если к одному из множителей прибавить вектор, коллинеарный другому множителю.
17. Чему равно векторное произведение противоположных векторов?
18. Равносильны ли равенства  и
и  ?
?
19. Дайте определение смешанного произведения векторов.
20. Сформулируйте условие компланарности векторов.
21. Докажите, что для любых заданных векторов  векторы
векторы  компланарны.
компланарны.
22. Покажите, что объем параллелепипеда, построенного на диагоналях граней данного параллелепипеда, равен удвоенному объему данного параллелепипеда.
23. Дайте геометрическое построение разложения вектора  на два компланарных с ним слагаемых, если известны:
на два компланарных с ним слагаемых, если известны:
а) длина и направление одного слагаемого;
б) направление обоих слагаемых;
в) направление одного и длина другого слагаемого.
Исследовать, когда разложение возможно, сколько имеет решений, если ни одно из слагаемых не параллельно  .
.
24. Дайте определение линейного оператора.
25. Дайте определение собственного вектора линейного оператора.
26. Дайте определение собственных значений линейных операторов.
27. Что называется линейным пространством?
28. Что называется Евклидовым пространством?
29. Дайте определение ортогональной системы векторов.

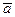 ={7; 6; –6} и
={7; 6; –6} и  ={6; 2; 9} могут быть взяты за ребра куба. Найти третье ребро.
={6; 2; 9} могут быть взяты за ребра куба. Найти третье ребро. ={1; 2; –1} и
={1; 2; –1} и  = {2; 0; –4}, совпадающие с двумя сторонами треугольника, найти угол при вершине А и площадь треугольника.
= {2; 0; –4}, совпадающие с двумя сторонами треугольника, найти угол при вершине А и площадь треугольника. и
и  , где А (3; 6; –2), В (6; –2; 3) могут быть взяты за ребра кеба. Найти конец С третьего ребра.
, где А (3; 6; –2), В (6; –2; 3) могут быть взяты за ребра кеба. Найти конец С третьего ребра. ,
,  могут быть взяты за ребра куба. Найти третье ребро.
могут быть взяты за ребра куба. Найти третье ребро. ,
,  , совпадающие со сторонами треугольника, найти угол при вершине А площадь треугольника.
, совпадающие со сторонами треугольника, найти угол при вершине А площадь треугольника. ,
,  , совпадающие с двумя сторонами треугольника, найти угол при вершине А и высоту ВD.
, совпадающие с двумя сторонами треугольника, найти угол при вершине А и высоту ВD.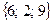 ,
,  могут быть взяты за ребра куба. Найти третье ребро.
могут быть взяты за ребра куба. Найти третье ребро. и
и  совпадают с двумя сторонами треугольника.Найти высоту, опущенную из вершины С.
совпадают с двумя сторонами треугольника.Найти высоту, опущенную из вершины С. и
и  =
=  могут быть взяты за ребра куба. Найти третье ребро.
могут быть взяты за ребра куба. Найти третье ребро. , если точка приложения ее перемещается из положения А(1; –1; 0) в положение В(1; 1; 1)?
, если точка приложения ее перемещается из положения А(1; –1; 0) в положение В(1; 1; 1)? приложена к точке А(2;1;-1). Определить направляющие косинусы момента этой силы относительно начала координат.
приложена к точке А(2;1;-1). Определить направляющие косинусы момента этой силы относительно начала координат. , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(2;-2;-1) в точку В(3;-2;-1)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(2;-2;-1) в точку В(3;-2;-1)? при перемещении точки ее приложения из М(2;4;-1) в N(0;1;0)?
при перемещении точки ее приложения из М(2;4;-1) в N(0;1;0)? приложена к точке А(3;4;5). Определить моменты этой силы относительно точки С(-1;0;-1).
приложена к точке А(3;4;5). Определить моменты этой силы относительно точки С(-1;0;-1). приложена к точке А(2;-1;1). Определить момент этой силы относительно начала координат.
приложена к точке А(2;-1;1). Определить момент этой силы относительно начала координат. при перемещении точки приложения силы из А(-1;1;1) в В(4;0;1).
при перемещении точки приложения силы из А(-1;1;1) в В(4;0;1). ,
,  ,
,  приложены к точке С(2;2;2). Определить величину момента равнодействующей этих сил относительно начала координат.
приложены к точке С(2;2;2). Определить величину момента равнодействующей этих сил относительно начала координат. , приложенной к точке А(-1;1;1) относительно точки В(0;3;-2).
, приложенной к точке А(-1;1;1) относительно точки В(0;3;-2).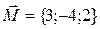 ,
,  ,
,  , приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения перемещается из А(1;2;1) в В(3;4;0).
, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения перемещается из А(1;2;1) в В(3;4;0). приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2). , когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(3;2;-4) в точку В(1;4;-3)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(3;2;-4) в точку В(1;4;-3)? приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2).
приложена к точке А(2;-1;0). Определить момент силы относительно точки В(-1;0;2). приложена к точке М(2;-1;3). Определить момент этой силы относительно точки А(-1;3;2).
приложена к точке М(2;-1;3). Определить момент этой силы относительно точки А(-1;3;2). приложена к точке А(1;-2;1). Определить величину момента этой силы относительно точки В(1;1;1).
приложена к точке А(1;-2;1). Определить величину момента этой силы относительно точки В(1;1;1). приложена к точке А(3;2;1). Найти момент этой силы относительно точки В(4;-3;7).
приложена к точке А(3;2;1). Найти момент этой силы относительно точки В(4;-3;7). , когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(2;-3;5) в точку В(-1;2;-4)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из точки А(2;-3;5) в точку В(-1;2;-4)? по перемещению материальной точки из А(1;0;1) в В(2;2;2).
по перемещению материальной точки из А(1;0;1) в В(2;2;2). приложена к точке М(4;2;-3). Определить момент этой силы относительно точки К(2;4;0).
приложена к точке М(4;2;-3). Определить момент этой силы относительно точки К(2;4;0).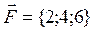 переместилась из А(-1;0;2) в В(3;4;1). Найти работу силы F.
переместилась из А(-1;0;2) в В(3;4;1). Найти работу силы F. приложена к точке М(4;-2;3). Определить момент этой силы относительно точки А(3;2;-1).
приложена к точке М(4;-2;3). Определить момент этой силы относительно точки А(3;2;-1). , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-1;3;2) в точку В(0;2;4).
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-1;3;2) в точку В(0;2;4). приложена к точке А(4;2;-4). Определить величину момента этой силы относительно начала координат.
приложена к точке А(4;2;-4). Определить величину момента этой силы относительно начала координат. , если ее точка приложения, двигаясь прямолинейно, перемещается из А(0;0;2) в В(0;2;0).
, если ее точка приложения, двигаясь прямолинейно, перемещается из А(0;0;2) в В(0;2;0). приложена к точке А(3;4;-3). Определить момент этой силы относительно В(0;1;1).
приложена к точке А(3;4;-3). Определить момент этой силы относительно В(0;1;1).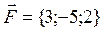 , когда точка ее приложения, двигаясь прямолинейно, перемещается из А(1;1;1) в В(2;-5;-7).
, когда точка ее приложения, двигаясь прямолинейно, перемещается из А(1;1;1) в В(2;-5;-7). приложена к точке А(4;2;-3). Найти величину момента этой силы относительно точки С(2;4;0).
приложена к точке А(4;2;-3). Найти величину момента этой силы относительно точки С(2;4;0). , когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-2;1;0) в В(3;2;-1)?
, когда ее точка приложения, двигаясь прямолинейно, перемещается из А(-2;1;0) в В(3;2;-1)? приложена к точке А(1;0;1). Найти момент этой силы относительно точки С(0;0;1).
приложена к точке А(1;0;1). Найти момент этой силы относительно точки С(0;0;1). и
и  , если коллинеарны векторы
, если коллинеарны векторы  и
и  ?
? и
и  ?
? векторы
векторы  компланарны.
компланарны.


