Описание работы схемы
Триггер Шмитта это компаратор, имеющий ПОС. В данной схеме доля выходного электрического сигнала ОУ поступает на прямой вход и устанавливает уровень, при котором схема будет переключаться. Принципиальная схема работы триггера Шмитта на ОУ изображена ниже.
ОУ подключен к двухполярному блоку питания на 5 вольт. На инверсный вход DA1 поступает синусоидный сигнал равный амплитуде 2 В. Сопротивления R1 и R2 имеют значения 25 кОм и 10 кОм. Напряжение на прямом выводе DA1 поступает с делителя напряжения построенного на резисторах R1 и R2, который подключен к выходу ОУ. Формула расчета для определения напряжения насыщения: 1. Uвх1 = +U*R2/(R1+R2) = 3,5*10/35 = 1 В 2. Uвх1 = -U*R2/(R1+R2) = -3,5*10/35 = -1 В Когда на выходе ОУ напряжение с положительным потенциалом насыщения – на прямом входе напряжение равно 1 вольту. Предположим, входной электрический сигнал постепенно увеличивается с нуля. Пока потенциал входного сигнала не превышает напряжения на прямом входе – схема находится в стабильном состоянии. Чуть только входной электрический сигнал превзойдет величину в 1 вольт, напряжение на входе ОУ сменит свою полярность на отрицательное напряжение насыщения. Это поменяет напряжение на прямом входе ОУ, и оно будет равно -1 вольт. Входной электрический сигнал постепенно будет увеличиваться до максимума, а затем начнет уменьшаться. После того как амплитуда сигнала на входе станет менее 1 вольта, то на выходе ОУ будет так же отрицательный потенциал насыщения. Как только сигнал на входе пройдет величину -1В, напряжение на выходе поменяется и будет равным положительному потенциалу насыщения. На графике можно наблюдать зависимость выходного напряжения триггера Шмитта от входного.
В результате такой работы схемы, шумы входного сигнала не будут влиять на выходной сигнал. · Формирование импульсов Формирователь коротких импульсов с применением линий задержки. Формирователь коротких импульсов формирует импульсы, длительность которых существенно меньше длительности исходных импульсов. Для построения схемы формирователя потребуются один элемент конъюнкции, один инвертор и линия задержки. Длительность выходного импульса формирователя определяется длительностью времени задержки линии задержки Dtз и средним временем распространения сигнала через инвертор tз срЭ1. На рис. 4.1 приведена схема формирователя, а на рис. 4.2, а, б – временные диаграммы, иллюстрирующие её работу. Из рис. 4.2, а следует, что для формирования импульса от переднего фронта (исходный импульс) необходимо подавать на линию задержки инвертированный импульс.
Рис. 4.1
Рис. 4.2
В случае формирования импульса от заднего фронта нужно инвертировать не задержанный (прямой) сигнал, т.е. сигнал, подаваемый на элемент «И», минуя линию задержки (рис. 4.2, б). Использование в формирователях линий задержки не всегда оправдано экономически и из конструктивных соображений. Если не требуется формирование строго определенной длительности коротких импульсов, в формирователях в качестве линии задержки применяются логические элементы (рис. 4.3). Так как каждый логический элемент обладает свойством задерживать распространение сигнала, то время задержки в такой схеме будет определяться числом используемых элементов логики n:
Dtз = tз срЭ1 + tз срЭ2 +....+ tз срЭn = n tз срЭ,
где tз срЭ – среднее время задержки одного логического элемента. Считается, что инвертор обладает значительно меньшим временем задержки сигнала; в качестве элементов задержки используются логические элементы с малым быстродействием.
Рис. 4.3 Формирователь импульсов на элементах логики с использованием RC цепи. RC цепи широко применяются в импульсной технике для формирования сигналов различной формы. RC-цепь – это цепь, состоящая из сопротивления R и конденсатора С. Постоянная времени этой цепи определяется как t = RC. В зависимости от сочетания соединений RС цепь может выполнять функцию как укорачивающей, так и удлиняющей цепи. Формирователь импульса с удлиняющей RC цепью и его временные диаграммы приведены на рис. 4.4, а, б соответственно.
Рис. 4.4
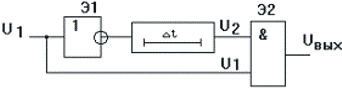
Длительность выработанного формирователем импульса можно вычислить исходя из условия разряда конденсатора С. Действительно, пока конденсатор С разряжается до уровня порогового напряжения Uпор, напряжение U2 воспринимается элементом Э2 как уровень логической «1» и на его выходе поддерживается «0». С течением времени tи напряжение на конденсаторе С становится равным Uпор и на выходе элемента Э2 появится «1». Если считать, что напряжение до начала разряда на конденсаторе было равно напряжению уровня «1», т. е. U1, то изменение напряжения Uс с течением времени можно представить как отсюда имеем
Длительность импульса равна времени разряда конденсатора до порогового значения Uпор:
Для ускоренного восстановления заряда конденсатора в схему может быть включен дополнительный диод D1 (рис. 4.4, а). Из-за большого обратного сопротивления диода его влияние в процесс разряда конденсатора можно не учитывать, т.е. разряд конденсатора будет осуществляться только через сопротивление R. В тех случаях, когда требуется получить импульсы большой длительности и в схеме используется конденсатор большой ёмкости, то последовательно с диодом включают дополнительное сопротивление Rдоб, ограничивающее ток заряда конденсатора. Величину сопротивления R выбирают исходя из следующих условий: · во-первых, величина сопротивления R не должна превышать максимально допустимого значения, при котором на этом сопротивлении за счет обратного входного тока элемента логики может создаться напряжение, сравнимое с напряжением Uпор (для элементов ТТЛ структуры максимальное значение Rмак = 2,2 кОм); · во-вторых, минимальное значение сопротивления ограничено допустимой нагрузочной способностью логического элемента Э1 и определяется как
где U1 – напряжение на выходе элемента Э1 в состоянии логической «1»; Номинал добавочного сопротивления имеет ограничение «снизу», и определяется из условия
где UпрD1 – прямое падение напряжения на диоде D1; I1доп – допустимый выходной ток элемента Э1 в состоянии логической «1».
где Rвых – выходное сопротивление первого элемента формирователя. · Мультивибраторы Мультивибратор — релаксационный генератор сигналов электрических прямоугольных колебаний с короткими фронтами. Термин предложен голландским физиком ван дер Полем, так как в спектре колебаний мультивибратора присутствует множество гармоник — в отличие от генератора синусоидальных колебаний («моновибратора»). Впервые мультивибратор был описан Икклзом и Джорданом в 1918 году. Мультивибратор является одним из самых распространённых генераторов импульсов прямоугольной формы, представляющий собой двухкаскадный резистивный усилитель с глубокой положительной обратной связью. В электронной технике используются самые различные варианты схем мультивибраторов, которые различаются между собой по типу используемых элементов (ламповые, транзисторные, тиристорные, микроэлектронные и так далее), режиму работы (автоколебательный, ждущие синхронизации), видам связи между усилительными элементами, способам регулировки длительности и частоты генерируемых импульсов и так далее. Приведенная схема мультивибратора на двух транзисторах сейчас почти не применяется, так как имеет плохие частотные свойства и не очень крутые фронты, что ограничивает частоту его генерации до единиц МГц. На более высоких частотах оба транзистора запираются и для восстановления работы устройство надо перезапускать, что во многих случаях неприемлемо. · · · Ждущий мультивибратор. Схема Обычное назначение ждущего мультивибратора – получение одиночного импульса заданной длительности. Отсчет длительности импульса начинается от фронта (или уровня) специального запускающего импульса. Для того, чтобы перейти от схемы автоколебательного к схеме ждущего мультивибратора, необходимо ввести дополнительно цепь запуска и цепь “торможения”. Схема одновибратора приведена на рис. 34а.
Рис. 34. Схема одновибратора (а) и временнaя диаграмма его работы (б) Если выходное напряжение ОУ отрицательное максимальное, то диод VD1 открыт, и напряжение на времязадающем конденсаторе u c небольшое отрицательное, равное примерно 0,5 В. При правильном выборе параметров схемы напряжение на неинвертирующем входе ОУ
поэтому при отсутствии запускающего импульса U зап схема находится в устойчивом состоянии. По приходе положительного запускающего импульса достаточной амплитуды операционный усилитель за счет положительной обратной связи переключается в такое состояние, при котором его выходное напряжение равно + U м. Диод VD2 закрывается и на р -входе ОУ устанавливается напряжение U п, определяемое выражением (37). К времязадающей цепи RC теперь приложено напряжение + U м, под действием которого закрывается диод VD2 и начинается заряд конденсатора С. Когда, спустя время t 1, напряжение u cдостигнет порога U п, операционный усилитель переключится и вернется в первоначальное состояние. Конденсатор С начнет разряжаться и, спустя промежуток времени t р, называемый временем релаксации, напряжение u c станет отрицательным, диод VD1 откроется и цикл закончится. Процессы в схеме описываются тем же уравнением (38), но начальное условие иное, и его решение для одновибратора имеет вид: u c(t) = U M - (U M + U Д)e -t/RC, где U Д – падение напряжения на открытом диоде VD1. Отсюда по условию u c(t 1) = U п найдем длительность импульса одновибратора: t 1 = RC ln{[1 + (R 1/ R 2)][1 + (U Д/ U М)]}. · Из последнего выражения видно, что длительность импульса одновибратора зависит от выходного напряжения насыщения ОУ, которое, в свою очередь определяется напряжением питания. Другим недостатком рассмотренной схемы является значительное время релаксации, в течение которого на одновибратор нельзя подавать запускающий импульс (иначе будет сокращена длительность выходного импульса). Эти недостатки отсутствуют у одновибратора, выполненного на специализированных ИМС, называемых аналоговыми таймерами. · Генератор линейно изменяющегося напряжения Генераторы линейно изменяющегося (пилообразного) напряжения (ГЛИН) применяют для развертки электронного луча в электроннолучевых трубках телевизионных, осциллографических и радиолокационных устройств, а также в схемах сравнения для задержки импульсов во временя и т. п. ГЛИН могут работать в режиме самовозбуждения и в ждущем режиме, когда период повторения пилообразного напряжения определяется запускающими импульсами. Режим самовозбуждения применяют, например, для получения непрерывной развертки в осциллографах, а ждущий режим - для получения ждущей развертки. Напряжением пилообразной формы называется напряжение, которое в течение определенного времени нарастает или убывает пропорционально времени (линейно), а затем быстро возвращается к исходному уровню. Пилообразное напряжение может быть линейно нарастающим (рис. 1) или линейно падающим (рис. 2).
Рис. 1 - Линейно изменяющееся нарастающее напряжение
Рис. 2 - Линейно изменяющееся падающее напряжение Пилообразное напряжение характеризуется длительностью прямого или рабочего хода tр.х.в течении которого напряжение изменяется линейно; длительностью обратного хода tо.х., в течении которого напряжение обычно изменяется по экспоненте, и амплитудой Umax. Принцип получения пилообразного напряжения заключается в медленном заряде (или разряде) кондера через большое сопротивление во время прямого хода и в быстром его разряде (или заряде) через малое сопротивление во время обратного хода. В упрощенном виде это показано на рисунке 3.
Рис. 3 - Принцип получения пилообразного напряжения Кондер С заряжается при разомкнутом ключе К через резик Rз, а разряжается при замкнутом ключе К через резик Rр. Такая схема не позволяет получить напряжения высокой линейности, поскольку повышение напряжения на кондере уменьшает зарядный ток. Для получения линейного напряжения кондер необходимо заряжать постоянным во все время заряда током. Поэтому смотрим на схемку:
Рис. 4 - Генератор пилообразного напряжения на транзисторах Электронный ключ собран на транзисторе VT1 и управляется импульсами положительной полярности, транзистор VT2 - эмиттерный повторитель - является следящей связью. В исходном состоянии, когда на входе отсутствует прямоугольный импульс (рис. 5), транзистор VT1 закрыт и кондер С3 заряжается. Ток заряда все время остается постоянным, т. к. напряжение на верхнем выводе R2 следит за напряжением на кондере С3 на его нижнем выводе. Диод VD1 закроется и в течение всего времени дальнейшего формирования линейного нарастания напряжения будет закрыт. Формируется рабочий ход пилообразного напряжения.
Рис. 5 - Формирование прямого и обратного хода При воздействии входного импульса транзистор VT1 открывается и кондер С3 быстро через него разряжается. Формируется обратный ход пилообразного напряжения. В это время кондер С2 подзаряжается до своего первоначального значения. · Введение в цифровую электронику · · Элементы алгебры логики Основные операции и элементы алгебры логики. Основой построения любого устройства, использующего цифровую информацию, являются элементы двух типов: логические и запоминающие. Логические элементы выполняют простейшие логические операции над цифровыми сигналами. Запоминающие элементы служат для хранения цифровой информации (состояния разрядов кодовой комбинации). Логическая операция состоит в преобразовании по определенным правилам входных цифровых сигналов в выходные. Математически цифровые сигналы обозначают поразрядно символами, например x1, x2, x3, x4. Их называют переменными. Каждая переменная может принимать значение "0" или "1". Результат логической операции часто обозначают F или Q. Он также может иметь значение "0" или "1". Математическим аппаратом логики является алгебра Буля. В булевой алгебре над переменными "0" или "1" могут выполняться три основных действия: логическое сложение, логическое умножение и логическое отрицание. [an error occurred while processing this directive] Логическое сложение (дизъюнкция или операция ИЛИ) записывается в виде
Правила выполнения операции ИЛИ заключаются в следующем:
Логические схемы, реализующие операцию ИЛИ; называют ячейками ИЛИ. Их схемное обозначение приведено на рис. 17.1а. Простейшая реализация логической ячейки ИЛИ на диодах приведена на рис. 17.1б. Напряжение на выходе схемы будет равно E (F=1), если хотя бы на один из входов будет подан единичный сигнал. Выбор типа выпрямителя.Так как однофазный мостовой двухполупериодный выпрямитель обладает рядом преимуществ по сравнению с другими схемами выпрямления, то его целесообразно выбрать в качестве схемы выпрямления. Логическое умножение (конъюнкция или операция И) записывается в виде
Правила выполнения операции И заключаются в следующем
Логическое отрицание (инверсия или операция НЕ) записывается в виде
и читается: F равно не x. Правила выполнения операции НЕ заключаются в следующем
Логические схемы, реализующие правило (17.3) называются ячейками НЕ. Их графическое обозначение приведено на рис. 17.3. Операция НЕ может быть реализована схемой транзисторного ключа. Рассмотренные логические правила и схемы позволяют реализовать сколь угодно сложную логическую функцию. Например, функция
реализуется пятью логическими элементами, в том числе два элемента И, два элемента НЕ и один элемент ИЛИ (см. рис. 17.4). Все логические элементы выпускаются в микросхемном исполнении. Они входят в состав всех серий цифровых микросхем и имеют следующие условные обозначения: элементы "ИЛИ" – ЛЛ; элементы "И" – ЛИ; элементы "НЕ" – ЛН. Например, микросхема К555 ЛИ1 имеет в своем составе 4 элемента "И" на два входа каждый.
· Теоремы алгебры логики Основные теоремы алгебры логики. Теоремы для одной переменной охватывают все операции над переменной x и константами "0" и "1":
Теоремы для двух или более переменных – x и y: Переместительный закон:
Сочетательный закон:
Распределительный закон:
Доказательство:
Здесь к скобке применена теорема 2. Закон поглощения:
Доказательство:
Доказательство:
Закон склеивания:
Доказательство:
Закон отрицания (теорема де-Морана)
· Булевы функции Булевы функции находят применение в конструировании и упрощении логических схем. Такие схемы встречаются в электронных устройствах, используемых в компьютерах, калькуляторах, телефонных системах и ряде других устройств. Обозначим множество {0;1} через Функция f из множества
Переменные булевых функций могут принимать только значения 0 или 1 и называются булевыми переменными. Множества всех булевых функции n переменных обозначается
Количество всех булевых функции n переменных находится по формуле
Например, булевых функции 1 переменной
булевых функции 2 переменных
булевых функции 3 переменных
Булевы функции часто задаются таблично. Эти таблицы напоминают таблицы истинности логических операций, поэтому сами булевы функции часто называют булевыми операциями, а соответствующие им таблицы - таблицами истинности. Булевы функции одной переменной
Булевы функции двух переменных
Как уже говорилось ранее, имеется 256 булевых функции 3 переменных. Перечислять их все нет необходимости, приведем лишь примеры задания такой функции:
Тема 3.2. Реализация функций формулами Так же, как составные высказывания строятся из более простых, с помощью логических операций, можно комбинировать булевы переменные с помощью булевых операций, получая булевы выражения, которые называются формулами. Всякой формуле однозначно соответствует некоторая функция, при этом говорят, что формула реализует функцию. ПРИМЕР Построить таблицу истинности для формулы
Таким образом, формула ПРИМЕР Построить таблицу истинности для формулы
Таким образом, формула Тема 3.3. Равносильные формулы Формулы называются равносильными, если реализуют одну и ту же функцию. Формула называется тождественно-истинной или тавтологией, если она реализует тождественную единицу. Формула называется тождественно-ложной, если она реализует тождественный ноль. Законы булевой алгебры Законами булевой алгебры называются следующие равносильности: 1. Идемпотентность
2. Коммутативность
3. Ассоциативность
4. Дистрибутивность
5. Закон поглощения
6. Закон склеивания
7. Закон нуля
8. Закон единицы
9. Закон дополнения
10. Инволютивность
11. Законы де Моргана
Тема 3.4 Принцип двойственности Двойственной для булевой функции
ПРИМЕР
Функция f называется самодвойственной если ПРИМЕР Функция ТЕОРЕМА (Закон двойственности) Если формула f 1 равносильна формуле f 2, то формула f 1* равносильна формуле f 2*. (Если две равносильные формулы заменить двойственными, то равносильность сохранится). ТЕОРЕМА (Принцип двойственности) Двойственная к булевой формуле может быть получена заменой констант 0 на 1, 1 на 0, Ù; на Ú;, Ú; на Ù; и сохранением структуры формулы (т.е. соответствующего порядка действий). · Минимизация булевых функций 3.Минимизация булевых функций Существуют несколько способов минимизации булевых функций.Прежде всего,это аналитический символьный и аналитический кодовый методы,метод Квайна - Мак-Класки,метод Блека - Порецкого,метод обобщенных кодов[11] и графическая минимизация с помощью карт Карно[12].Пример для демонстрации аналитических методов:z = x_y+xy_+xy = (x_y+xy)+(xy_+xy) = y(x_+x) + x(y_+y) = x+y.z = 01+10+11 = (01+11)+(10+11) = -1+1- = x+y.Первые четыре метода чрезвычайно громоздки и малоэффективны уже при количестве аргументов более четырёх. Метод обобщенных кодов ориентирован на использование ЭВМ,однако может использоваться и при ручном синтезе для функций от большого числа переменных. 3.1.Минимизация полностью определенных булевых функций Наиболее эффективна минимизация булевых функций с помощью картКарно.До сих пор существует ошибочное мнение,что этим методом можнорешать задачи для функций от не более, чем 6 аргументов. На самом делекарты Карно могут применяться для функций даже от 8-12 переменных[12]. На рис.3.1. представлены карты Карно для 2-6 переменных и приме-ры минимизации с их помощью логических функций. \ x1 \x2x1 \x2x1 x2 \ 0 1 x3\ 00 01 11 10 x4x3\ 00 01 11 10 \ ----T----- -----T----T----T----- ------T-----T-----T------ 0 | а | а | 0 | а | | | а | 00 | 1 | 0 | 1 | 1 | +----+----+ +----+----+----+----+ +-----+-----+-----+-----+ 1 | | | 1 | | | | | 01 | 0 | 0 | 1 | 0 | L----+----- L----+----+----+----- +-----+-----+-----+-----+ -- -- -- 11 | 0 | 0 | 1 | 0 | а = X2 а = X3*X1 +-----+-----+-----+-----+ 10 | 1 | 0 | 1 | 1 | L-----+-----+-----+------ -- -- y = X2X1 + X3*X1 а) б) в) \ \ X2X1 X5X4X3 \ 00 01 11 10 ------T-----T-----T------ 000 | а | а | b | b | +-----+-----+-----+-----+ -- -- 001 | | | b | b | а = X3*X2 +-----+-----+-----+-----+ -- 011 | | | b | b | b = X5*X2 +-----+-----+-----+-----+ 010 | а | а | b | b | c = X5*X3*X2 +-----+-----+-----+-----+ 110 | а | а | | | +-----+-----+-----+-----+ 111 | | | с | с | +-----+-----+-----+-----+ 101 | | | с | с | +-----+-----+-----+-----+ 100 | а | а | | | L-----+-----+-----+------ г) \ Х3Х2Х1 Х6Х5Х4 \ 000 001 011 010 110 111 101 100 ----T---T---T---T---T---T---T---- 000| a | в | c | | | c | в | a | +---+---+---+---+---+---+---+---+ 001| e | | | e | | | | | f=X6*X5*X4 +---+---+---+---+---+---+---+---+ __ 011| m | k | k | m | m | k | k | m | n=X6*X4*X2 +---+---+---+---+---+---+---+---+ 010| d | d | | | | | d | d | +---+---+---+---+---+---+---+---+ 110| n | n | | | | | n | n | +---+---+---+---+---+---+---+---+ 111| f | f | f | f | f | f | f | f | +---+---+---+---+---+---+---+---+ 101| | | | | | | | | +---+---+---+---+---+---+---+---+ 100| n | n | | | | | n | n | L---+---+---+---+---+---+---+---- д) Рис.3.1. Карты Карно для 2-6 переменных Метод Карно основан на законе склеивания.Склеиваются наборы,отличающиеся друг от друга лишь значением одного разряда. Такие наборы называются соседними, и они соответствуют соседнимклеткам карты Карно.Формируются такие наборы(коды Грея) по принципусимметрии[11,12]. Введем определение прямоугольника Карно, под которым будем пони-мать некоторую, зачастую разрозненную, фигуру покрытия,удовлетворяющуюпринципу симметрии,т.е. сплошь состоящую из элементарных прямоугольни-ков Карно,закодированных только соседними наборами. Алгоритм "НИИРТА" графической минимизации логических функций 1.Заполнить карту Карно нулями и единицами в соответствии с таб-лицей истинности. 2.Покрыть все единичные наборы минимальным количеством прямоу-гольников Карно, каждый из которых имеет максимальную площадь. 3.Каждому прямоугольнику Карно соответствует одна импликанта,причем, если в границах прямоугольника Карно какая-либо переменнаяпринимает значение как 0, так и 1, то она склеивается. На рис. 3.2 представлены фигуры покрытия,не являющиеся прямоу- гольника Карно \ x3x2x1 x5x4 \ 000 001 011 010 110 111 101 100 ----T---T---T---T---T---T---T---- 00 | К | К | | К | К | | К | К | | | | | | | | | | +---+---+---+---+---+---+---+---+ 01 | П |П | | | | | | | | | | | | | | | | +---+---+---+---+---+---+---+---+ 11 | | | | М |М |М |М | | | | | | | | | | | +---+---+---+---+---+---+---+---+ 10 | П |П | | М |М |М |М | | | | | | | | | | | L---+---+---+---+---+---+---+---- Рис. 3.2 Фигуры покрытия,не являющиеся прямоугольниками Карно Применим карту Карно для решения задачи 2.1 о синтезе автоматадля тайного голосования.Это решение представлено на рис. 3.3 \ x2x1 x4x3 \ 00 01 11 10 ----T----T----T----- 00 | 0 | 0 | 0 | 0 | y= x4x1 + x4x2 + x4x3 + x3x2x1 +----+----+----+----+ 01 | 0 | 0 | 1 | 0 | Это выражение представляет собой пример +----+----+----+----| минимальной дизъюнктивной нормальной 11 | 1 | 1 | 1 | 1 | формы (МДНФ). +----+----+----+----+ 10 | 0 | 1 | 1 | 1 | L---------+---------- Рис. 3.3. Решение задачи 2.1. В некоторых случаях приведение результата минимизации к скобочнойформе позволяет уменьшить сложность булевой функции. Скобочная формадля (3.3) имеет вид y= x4(x1 + x2 + x3) + x3x2x1. Реализация скобочной формы логической функции автомата для тайно-го голосования в виде релейной схемы изображена на рисунке. | x3 x2 x1 |+----------------L-----L------L-------------- || | ------- || x4 x3 | | | |+------L---T-----L-----T--------------------+---+ УИ +----+| | x2 | | | || +-----L-----+ L------ || | x1 | || L-----L------ || ||+Еп |-Еп Релейная схема автомата к задаче 2.1 На схеме представлены контакты реле x4,x3,x2,x1.При включениитумблера срабатывает соответствующее реле и замыкает свои контак-ты.Например,если за прием абитуриента проголосовали председатель(x4) и3-й член комиссии(х3),то замкнутся контакты х4 и х3 и сработает уст-ройство индикации(УИ),запитанное от источника с напряжением Еп.· Комбинационные устройства Логические устройства разделяют на два класса: комбинационные и последовательностные. Устройство называют комбинационным, если его выходные сигналы в некоторый момент времени однозначно определяются входными сигналами, имеющими место этот момент времени. Иначе устройство называют последовательностным или конечным автоматом (цифровым автоматом, автоматом с памятью). В последовательностных устройствах обязательно имеются элементы памяти. Состояние этих элементов зависит от предыстории поступления входных сигналов. Выходные сигналы последовательностных устройств определяются не только сигналами, имеющимися на входах в данный момент времени, но и состоянием элементов памяти. Таким образом, реакция последовательностного устройства на определенные входные сигналы зависит от предыстории его работы. · · Принцип работы шифратора Шифратор – это логическое устройство, выполняющее преобразование позиционного кода в n разрядный двоичный код, например для преобразования чисел из десятичной системы в двоичную. Таким образом, шифратор – это комбинационное устройство, реализующее обратную дешифратору функцию. Рассмотрим логическую схему шифратора на два выхода (рис. 2.4, а) и ее условное обозначение (рис 2.4, б). В соответствии с таблицей истинности (рис. 2.4, в), связь выходных и входных сигналов описывается выражениями: Y0=X1+X3; Y1=X2+X3. а б в
Рис. 2.4
Нетрудно видеть, что в шифраторе сигнал, подаваемый на вход X0, не используется. Примером шифратора может служить микросхема К555ИВ3. · Дешифратор принцип работы Линейный или одноступенчатый дешифратор. Дешифратор – это комбинационное устройство, предназначенное для преобразования параллельного двоичного кода в унитарный, т.е. позиционный код. Обычно указанный в схеме номер вывода дешифратора соответствует десятичному эквиваленту двоичного кода, подаваемого на вход дешифратора в качестве входных переменных, вернее сказать, что при подаче на вход устройства параллельного двоичного кода на выходе дешифратора появится сигнал на том выходе, номер которого соответствует десятичному эквиваленту двоичного кода. Отсюда следует то, что в любой момент времени выходной сигнал будет иметь место только на одном выходе дешифратора. Этот сигнал, в зависимости от типа дешифратора, может иметь как уровень логической единицы (при этом на всех остальных выходах – уровень логического 0), так и уровень логического 0 (при этом на всех остальных выходах – уровень логической единицы). Рассмотрим пример синтеза дешифратора 3
Таблица состояний дешифратора
Как следует из таблицы состояний, каждой функции соответствует только один разряд в выходном коде, следовательно, не требуется минимизировать эти функции (рис. 2.1).
Рис. 2.1 Для реализации полного дешифратора на m входов (переменных) потребуются n = 2m элементов конъюнкции (количество входов каждого элемента «И» равно m) и m элементов отрицания. Промышленностью России выпускаются различные модификации дешифраторов в интегральном исполнении. Приведем обозначение дешифраторов на принципиальных схемах (рис. 2.2, а) и таблицу истинности (рис. 2.2, б). а Рис. 2.2
|






 ,
,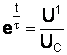 .
. .
.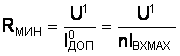
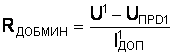 ,
, Рис. 4.5
Рис. 4.5
 ,
,
 Принципиальная схема «классического» простейшего транзисторного мультивибратора
Принципиальная схема «классического» простейшего транзисторного мультивибратора 
 ,
,

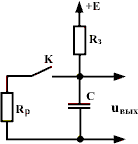





 (17.2) [an error occurred while processing this directive]
(17.2) [an error occurred while processing this directive]
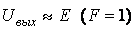 только в том случае, если все диоды будут закрыты, т. е. на всех входах будет потенциал Е (логическая 1). В противном случае открывшийся диод шунтирует нагрузку и
только в том случае, если все диоды будут закрыты, т. е. на всех входах будет потенциал Е (логическая 1). В противном случае открывшийся диод шунтирует нагрузку и  .
.

 (17.3)
(17.3)




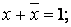
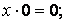




















 , т. е.
, т. е.  .
. называется булевой функцией n переменных. Напомним, что
называется булевой функцией n переменных. Напомним, что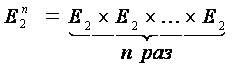
 , т.е.
, т.е. .
. .
. ,
, ,
, .
.
 , ·
, ·
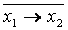
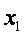


 ,
, 


 ,
,  , ~
, ~
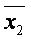




 ,
, (тождественная единица) и др.
(тождественная единица) и др. .
.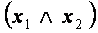

 реализует функцию
реализует функцию  (тождественная единица).
(тождественная единица). .
.

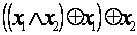
 реализует функцию
реализует функцию  (дизъюнкция).
(дизъюнкция). .
. .
. .
. .
. .
. .
. .
. .
. .
.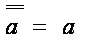 .
. .
. называется булева функция
называется булева функция .
. ,
, 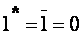 ,
,  ,
, ,
, .
. .
. является самодвойственной, т.к.
является самодвойственной, т.к.  .
.
 8, следовательно, количество разрядов двоичного числа – 3, количество выходов – 8.
8, следовательно, количество разрядов двоичного числа – 3, количество выходов – 8.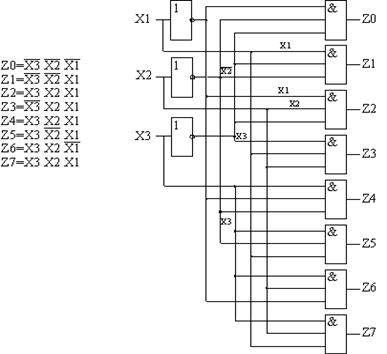
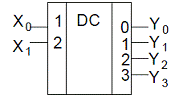 б
б 



