Амплитудно-частотная характеристикаРассмотрим амплитудно-частотную характеристику усилителя (АЧХ). Очевидно, что для этого нужно построить зависимость амплитуды (коэффициента усиления) от частоты в двойном логарифмическом масштабе. Почему? Потому что сложные зависимости амплитуды от частоты в двойном логарифмическом масштабе превращаются в простые. Пример представлен на рис., верхняя кривая:
Для одиночного каскада, у которого верхнее и нижнее ограничение по частоте обычно связано с одной RC- цепочкой, нарастание и спад коэффициента усиления связано с частотой пропорционально (рост пропорционален f, спад обратно пропорционален f). В двойном логарифмическом масштабе и то и другое будет идти по прямой, наклонённой под 450 к горизонтали. Другое удобство заключается в том, что двойной логарифмический масштаб полезен при больших изменениях частот и коэффициентов усиления. Ещё нам надо будет искать сигнал, равный 0,7 от Кмакс. Это значит, что нужно отступить вниз от Кмакс на один и тот же шаг вне зависимости от того, чему равен Кмакс. Итак, у нас есть кривая К0, это верхняя кривая на рис., которая описывает частотные свойства усилителя без обратной связи. Надо отступить от максимального значения К0 на уровень 0,7 – этот уровень и определяет нижнюю и верхнуюю частотные границы, а их разность - Df0 это полоса частот. Что же будет при использовании ООС? Надо применить уже известную формулу. Если ВК0>>1, то Кос=1/В. В противном случае Кос<K0. С учётом этого, в двойном логарифмическом масштабе кривая обрежется уровнем 1/В, как это показывает кривая Кос. Отступив на ту же величину 0,7, получим новую полосу частот βfос . Очевидно, это гораздо большая полоса частот. Улучшится также и сама частотная характеристика. Например, у нас плохая, неравномерная характеристика, как на рис. ниже.
Очевидно, неравномерности частотной характеристики уменьшатся в F раз.
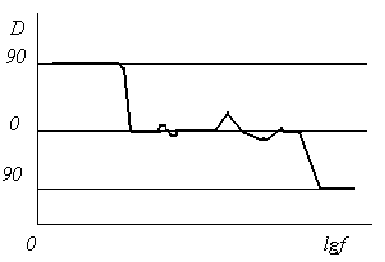
Известно, что при наличии амплитудно-частотной неравномерности имеется ещё и фазо-частотная неравномерность. Например, для характеристики на последнем рис. фазовая характеристика будет как на верхнем рис. При применении ООС кривая сгладится так, что там, где ООС действует (глубина обратной связи велика), там фаза будет стремится к нулю, см. рис.
Понять это можно из следующих рассуждений. Если мы учитываем в формуле для коэффициента усиления также и сдвиг фаз, то это комплексные коэффициенты усиления. Напишем уравнение для комплексных коэффициентов усиления, обозначив комплексные величины точкой сверху:
исключая отсюда х и пренебрегая синусом (считаем, что углы малые), получим, что сдвиг фазы при наличии ООС уменьшается в глубину обратной связи F. До сих пор мы нигде не учитывали, что усиление по напряжению. Можно было бы сказать, что коэффициент усиления по току, и всё осталось бы точно так же. То есть всё, что мы обсудили про положительное влияние ООС, будет справедливо и для усилителей токов. Но есть параметры усилителей, которым это не всё равно. Это – входное и выходное сопротивления. Для того, чтобы понять, как влияет ООС на них, рассмотрим четыре разных случая. 1. Последовательная обратная связь по напряжению. Что это значит? Попросту это значит, что часть выходного напряжения снимается с нагрузки и прибавляется к входному напряжению.
мы видим, что входное сопротивление увеличивается в глубину обратной связи. Выходное сопротивление наоборот уменьшается в F раз. 2. Последовательная обратная связь по току. На входе сигнал подаётся по напряжению, с выхода он снимается пропорциональный току.
В этом случае входное сопротивление также растёт
Иначе обстоит дело в выходным сопротивлением: в этом случае мы видим, что и входное, и выходное сопротивление велики, примерно в F раз больше, чем у обычного усилителя. 3. Параллельная обратная связь по току. В этом случае часть выходного тока подаётся на вход и вычитается из входного тока. Поэтому результат будет как в таблице.
Входное сопротивление уменьшается, а выходное сопротивление увеличивается. 4. Параллельная обратная связь по напряжению. В этом случае на входе прибавляется ток, а с выхода снимается напряжение.
В этом случае и входное, и выходное сопротивления уменьшаются примерно в F раз. Мы уже убедились, что ООС при больших коэффициентах усиления (от 1000 до 1000 000) и глубокой обратной связью F > 100 очень полезна: хоть коэффициент усиления и становится меньше, но зато улучшаются частотные Почему это происходит? Дело в том, что ООС – это когда сдвиг фазы между входом и выходом составляет 1800. Но усилителей с бесконечно большой полосой частот не бывает – где-то бывает спад частотной характеристики. При этом известно, что если в двойном логарифмическом масштабе рост или спад идёт под углом в 450 , то добавляется или отнимается сдвиг фазы 900. А если усилитель двухкаскадный, то будет 1800. Но в сумме это уже 3600 – то-есть получается вместо ООС ПОС – положительная обратная связь. Если при этом и коэффициент усиления больше 1, то получится генератор. Эту ситуацию иллюстрирует рис. Есть простой метод борьбы с этим явлением. Нужно в выходном каскаде усилителя поставить ёмкость, так, чтобы она ограничивала коэффициент усиления так, чтобы спад характеристики был под 450 при большом коэффициенте усиления. · Усилитель с общим коллектором На рис. 24.3(а) показан усилитель, где транзистор включен по схеме с общим коллектором. Здесь С 1 и С 2 – входной и выходной разделительные конденсаторы, резисторы R 1 и R 2 образуют цепь смещения по постоянному току. Коллекторный резистор отсутствует, так как выходной сигнал снимается с эмиттера. На рис. 24.3(б) представлен обычный способ изображения схемы усилителя с ОК. Выходной сигнал действует на эмиттерном резисторе R 3, и поэтому данная схема называется эмиттерным повторителем. Эмиттерный повторитель имеет высокий коэффициент усиления по току и меньший единицы коэффициент усиления по напряжению. Такое значение коэффициента усиления по напряжению связано с действием 100 %-ной отрицательной обратной связи через резистор R 3.
|
свойства, линейность усилителя, фазовые характеристики и т.д. Но бывает, что при охвате ООС усилителя с большим числом каскадов часто возникает самовозбуждение, и усилитель превращается в генератор.
