Фазовые соотношения
При увеличении входного сигнала потенциал базы увеличивается относительно потенциала эмиттера, т. е. увеличивается напряжение V BE, и соответственно увеличивается падение напряжения на эмиттерном резисторе, являющегося выходным напряжением. Таким образом, усилитель с ОК не изменяет фазу входного сигнала при его усилении.
Рис. 24.3. Эмиттерный повторитель, или усилитель с ОК, (а) и стандартное изображение его схемы (б). Таблица 24.1. Сравнение усилителей с ОЭ, ОБ и ОК
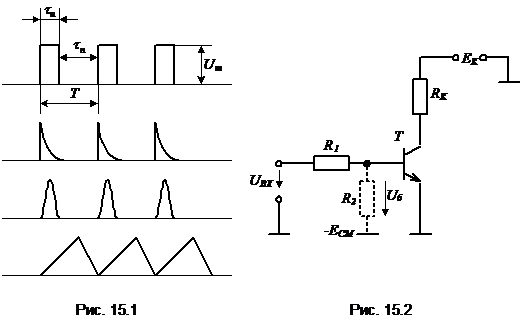
· Импульсный сигнал · Электрическим импульсом называется кратковременное отклонение тока или напряжения от исходного уровня. Графически импульсы изображаются на временных диаграммах – зависимости величины тока или напряжения от времени. Импульсные сигналы бывают двух видов: видеоимпульс и радиоимпульс. Различаются они отсутствием или наличием высокочастотного заполнения. На практике редко встречаются одиночные импульсы. Как правило, применяются несколько импульсов следующие один за другим – последовательности импульсов. Последовательности импульсов бывают периодические, квазипериодические и непериодические: Последовательность импульсов периодическая, если каждый последующий импульс отстоит от предыдущего на одно и тоже значение. Последовательность называется квазипериодической, если выполняется условие периодичности для одного или нескольких параметров. Последовательность называется непериодической, если не выполняется условие периодичности ни для одного параметра. Для описания импульсов применяют различного рода параметры: 1. Основные. 2. Производные. 3. Дополнительные. Основные. Амплитуда импульсов Um, длительность импульса tи, период следования Т. См.рис.2а. Производные. Производные параметры можно получить из основных – частота F=1/T [Гц], скважность импульсов – q=T/tи показывает сколько импульсов умещается в 1 периоде, например, для меандра q=2(меандр –такой вид последовательности импульсов у которой длительность равна паузе). Дополнительные. К дополнительным параметрам прибегают для описания импульсов непрямоугольной формы: А – высота (амплитуда) импульса, DА – спад вершины импульса, kсп = DА/А – коэффициент спада, tи0 – длительность импульса, tф0 – длительность фронта импульса, tс0 – длительность среза импульса, tи – активная длительность импульса, измеренная на уровне 0,5Um. При не столь явном переходе от переднего фронта к вершине вводят активные длительности фронта и среза – tф и tс. Их Для описания пилообразного импульса используют следующие параметры (рис.3в): t п.х .- время прямого хода, tо.х. – время обратного хода, скорость нарастания импульса – VUп.х.=Um/ tп.х.,коэффициент нелинейности kн=1-tgj0/tgj1 Для математического описания импульсов непрямоугольной формы наиболее часто прибегают к экспоненциальной функции. Его форма описывается разностью двух экспонент: u(t) = A(e-b1t - e-b2t). Постоянные времени 1/b2 и 1/b1 описывают восходящую и падающую части импульса. Определим активные длительности tи и tф импульса. Опуская промежуточные вычисления, получим: tи =(2/g+0,78)/j1 tф = 0,55ln(g/(g-1)), где g=b2/b1. Особую роль в технике приема импульсных сигналов играет колокольный импульс. При такой форме наиболее удачно сочетаются требования сосредоточения энергии импульса как во времени, так и в спектре. Его форма определяется функцией u(t) = Легко найти для такой формы активные длительности tи и tф импульса. tи =1,66/b, tи =0,72tи. Представление импульсов во временной области позволяет определять его параметры, энергию, мощность, но не является единственно возможной. Нередко уделяется большое внимание частотным свойствам сигналов. Для этого используется представление сигналов в частотной области в виде спектра, получаемого на основе математического аппарата преобразования Фурье. Знание частотных свойств позволяет решать задачи идентификации сигнала, его фильтрации и т.д. Одним из важнейших частотных характеристик сигнала является ширина его спектра.
A -
0 t <-
-
Частотный спектр этой функции определяется интегралом Фурье: f(w) = =
Амплитудно-частотный спектр одиночного прямоугольного импульса приведен на рис.4. По оси ординат отложены относительные значения амплитуд гармоник в единицах А Разность частот между соседними гармониками Dw=2p/T, где Т – период следования импульсов. Для одиночного импульса Т= Возвращаясь к спектру одиночного импульса можно заметить, что чем короче импульс (меньше · Основные характеристики импульсных сигналов Для количественной оценки формы импульса и его энергетических показателей вводят следующие основные параметры: 1. Амплитуда импульса Um – максимальное значение ВИ данной формы; 2. Длительность импульса tи – промежуток времени между возникновением и исчезновением импульса, измеряемый либо по длительности основания, либо на уровне 0.1Um либо на уровне 0.5Um (активная длительность). Диапазон длительностей ВИ в промышленной автоматике лежит в пределах от 0,001мкс до 1с. 3. Длительность фронта tф (переднего фронта) или tc (заднего фронта) соответственно равные времени нарастания от 0.11Um до 0.9Um или спада от 0.9Um до 0.1Um импульса. Иногда вводят крутизну фронтов (среза) S отношение амплитуды к tф или tc. 4. Спад вершины импульса 5. Период повторения импульсов Т – отрезок времени между началом (концом) двух соседних однополярных ВИ. 6. Частота повторения (следования) 7. Скважность импульса Q - отношение периода Т к длительности tu.
Для прямоугольного импульса справедливы выражения:
Мощность Pи в импульсной технике называют мощностью в импульсе. Если в спецустройстве непрерывно накапливать отдаваемую источником питания мощность, а во время импульсов отдать её, то мощность в импульсе может быть в Q раз больше мощности источника питания! Т. е. Действующее значение импульса (напряжения, тока, мощности) находят:
где В таблице приведены значения Pср, Uср и Uэф для некоторых импульсов различной формы.
· · Транзисторный ключ принцип работы Устройства, выполняющие обработку импульсных сигналов, называются импульсными устройствами. Среди различных импульсных устройств видное место занимают электронные ключи. Через идеальный разомкнутый ключ ток не протекает. Напряжение на идеальном замкнутом ключе равно нулю. Смена состояния ключа происходит под действием сигналов, подаваемых на один или нескольких входов. · Работа компаратора Во многих описаниях компаратор сравнивается с обычными рычажными весами, как на базаре: на одну чашу кладется эталон – гири, а на другую продавец начинает подкладывать товар, например, картошку. Как только вес товара становится равным весу гирь, точнее чуть больше, чашка с гирями устремляется вверх. Взвешивание закончено. То же самое происходит и с компаратором, только в этом случае роль гирь выполняет опорное напряжение, а в качестве картошки используется входной сигнал. Как только на выходе компаратора появляется логическая единица, то считается, что сравнение напряжений произошло. Вот это и есть то самое «чуть больше», которое в справочниках называется «пороговая чувствительность компаратора».
|





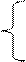 Найдем частотный спектр одиночного прямоугольного импульса, описываемого следующей функцией: U
Найдем частотный спектр одиночного прямоугольного импульса, описываемого следующей функцией: U /2< t <
/2< t < 


 =
= =
=  =
= 
 , следовательно, спектр непрерывный. При увеличении числа импульсов в последовательности спектр, приобретает характер линейчатого. Если количество импульсов в последовательности равно 20-30, то спектр, практически можно считать линейчатым. Он состоит из отдельно стоящих компонент спектра, разделенных полосами частот Dw.
, следовательно, спектр непрерывный. При увеличении числа импульсов в последовательности спектр, приобретает характер линейчатого. Если количество импульсов в последовательности равно 20-30, то спектр, практически можно считать линейчатым. Он состоит из отдельно стоящих компонент спектра, разделенных полосами частот Dw. (желательно иметь как можно меньшим!) Относительная величина спада
(желательно иметь как можно меньшим!) Относительная величина спада  . У треугольных, пилообразных ВИ вершины нет, а фронт сразу переходит в срез.
. У треугольных, пилообразных ВИ вершины нет, а фронт сразу переходит в срез. , обратная величине T (колеблется от долей Гц до десятков МГц).
, обратная величине T (колеблется от долей Гц до десятков МГц). – величина безразмерная и всегда больше 1. Одна из энергетических характеристик импульсного устройства, так как отражает накопление больших энергий во время большой паузы и её генерирования во время кратковременного импульса. Величина, обратная скважности, называется коэффициентом заполнения импульсов:
– величина безразмерная и всегда больше 1. Одна из энергетических характеристик импульсного устройства, так как отражает накопление больших энергий во время большой паузы и её генерирования во время кратковременного импульса. Величина, обратная скважности, называется коэффициентом заполнения импульсов: 


 (61)
(61)
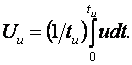
 (62)
(62)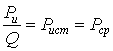 .
.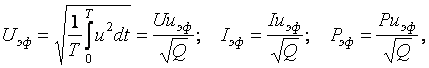 (63)
(63) – действующее значение соответствующей величины за время t и для прямоугольных импульсов:
– действующее значение соответствующей величины за время t и для прямоугольных импульсов:  .
.
 . Мощность теряемая в транзисторе Ротс =Iкэ о ×Uк мала, так как мал ток.
. Мощность теряемая в транзисторе Ротс =Iкэ о ×Uк мала, так как мал ток. . Для этого часто применяют дополнительный источник смещения - Есм и резистор R 2 (пунктир на рис.15.2) При таком включении напряжение смещения создается двумя источниками Есм и источником тока Iкэ о, т.е.
. Для этого часто применяют дополнительный источник смещения - Есм и резистор R 2 (пунктир на рис.15.2) При таком включении напряжение смещения создается двумя источниками Есм и источником тока Iкэ о, т.е. . (15.1)
. (15.1) ,
,
 . (15.2)
. (15.2) . (15.3)
. (15.3)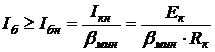 . (15.4)
. (15.4) .
. . (15.5)
. (15.5)


