ЛАБОРАТОРНАЯ РАБОТА № 5. ЦЕЛЬ РАБОТЫ: научиться определять скорость звуковой волны.
ОПРЕЛЕЛЕНИЕ СКОРОСТИ ЗВУКА МЕТОДОМ СТОЯЧЕЙ ВОДЫ
ЦЕЛЬ РАБОТЫ: научиться определять скорость звуковой волны. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: звуковой генератор, осциллограф, измерительная труба с телефоном и микрофоном. 1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Звуковые волны в воздухе являются продольными, т. е. такими, у которых смещение колеблющихся частиц среды происходит вдоль направления распространения волны. Распространение звуковых волн сопровождается при этом возникновением ряда чередующихся сгустков и разряжений воздуха и характеризуется определенной скоростью. Скорость звука измеряется расстоянием, на которое звуковая волна распространяется за одну секунду. Длина бегущей волны λ определяется расстоянием, на которое распространяется звуковой процесс за время одного полного колебания звучащего тела, а частотой колебания называется число колебаний за одну секунду. Поэтому скорость звука
Это соотношение и используется в работе для определения скорости звука. В данной работе нас интересует случай, когда складываются две встречных волны с одинаковой частотой и амплитудой. Допустим, что бегущая волна достигает границы среды и отражается. Отраженная волна распространяется в обратном направлении, складываясь в каждой точке среды с падающей волной. Если затухание в среде мало, то амплитуда падающей и отраженной волн практически одинаковы, но фазы колебаний различны, так как падающая волна, и волна отраженная, проходят различные пути до точки сложения. Если граница со средой, от которой происходит отражение, закреплена, то отраженная волна изменяет свою фазу на Если же волна падает на свободную границу, за пределом которой упругая среда отсутствует, то фаза волны при отражении не изменяется и потери полуволны не происходит. Если участок, в котором распространяется волна, ограничен с двух сторон закрепленными границами, то стоячая волна должна иметь на обеих границах узлы (рис.1, а). Следовательно, стоячие волны образуются на участке с закрепленными границами, когда на нем укладывается целое число полуволн. В случае, если обе границы свободны /рис.1/, то на них образуются пучности. Стоячие волны образуются на участке среды со свободными границами, когда на нем укладывается целое число полуволн. И, наконец, если одна граница участка закреплена, а вторая свободна, то на первой образуется узел, а на второй- пучность /рис.1,в/.Стоячие волны образуются на участке среды, одна граница которого закреплена, а вторая свободна, когда на участке укладывается нечетное число четвертей волн.
Рис.1 Предположим, что падающая и отраженная плоские волны распространяются в среде без затухания, обладая одинаковой амплитудой α0.Выберем ось x совпадающей с одним из лучей. Начало координат поместим в точке, в которой обе волны имеют одну фазу, и начнем счет времени от момента, когда фазы обеих волн равны нулю. Тогда уравнение падающей волны будет иметь вид: Yл= αо...Sinω(t- а отраженной, распространяющейся в направлении, противоположном направлению положительного отсчета х:
Y0=αoSinω(t+ Результирующее смещение: У=Ул+Уо=2*αоSin(2π Из равенства (4) видно, что если мы зафиксируем некоторую точку, имеющую координату Х1, то получим для частицы, находящейся в этой точке, уравнение гармонического колебания с амплитудой α = 2αоSin α = 2αо*Sin2π В точках, где Sin 2π где n = 0, 1, 2.... Следовательно, координаты узловых точек: Xy = Расстояние между соседними узловыми точками: Xy, n+2 – Xy, n= Положение пучностей определяется условием: 2π и координаты пучностей будут: Xпуч = ± (2π + 1) Расстояние между соседними узлом и пучностью: Xyз – Хпуч = Таким образом, зная расстояние между двумя соседними узлами и пучностями можно легко определить длину звуковой волны
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Рис.2 Схема экспериментальной установки изображена на рис. 2. Телефон Т, получая электрический сигнал от генератора 1, излучает звуковые волны в трубку 2. Достигнув микрофона М, звуковая волна преобразуется в напряжение, которое поступает вертикально отклоняющие пластины У электронного осциллографа 3. Напряжение на вертикально отклоняющие пластины Х подается непосредственно с входных клемм звукового генератора. Телефон жестко закреплен на левом конце трубы, а микрофон может свободно перемещаться внутри нее. Фазовый сдвиг сигнала, поступающего на пластины У, относительно сигнала, подведенного к пластинам Х, зависит от времени, который тратит звук на прохождения, расстояния между телефоном и микрофоном. Поэтому величина сдвига фаз, происходящая при изменении расстояния между микрофоном и телефоном, может быть использована для определения длины волны λ. При включении установки на экране осциллографа должен быть виден эллипс. Изменяя расстояние между микрофоном и телефоном, можно добиться превращения эллипса в прямую линию. Если теперь сместить микрофон на
|

 связана с частотой колебания u простой зависимостью.
связана с частотой колебания u простой зависимостью. (1)
(1) , т. е. направление смещений при отражении изменится на противоположное. Это явление называют «потерей полуволны» при отражении.
, т. е. направление смещений при отражении изменится на противоположное. Это явление называют «потерей полуволны» при отражении.
 )=αo*Sin2π (ut-
)=αo*Sin2π (ut-  ) (2)
) (2) t=2αoSin(2π
t=2αoSin(2π  и с фазой 2πut. Если мы будем переходить от одной точки к другой, то амплитудой будет меняться по закону:
и с фазой 2πut. Если мы будем переходить от одной точки к другой, то амплитудой будет меняться по закону: . (6)
. (6)
 (7)
(7)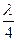 (8)
(8) , а скорость звука вычислить по формуле (1).
, а скорость звука вычислить по формуле (1).
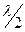 , то на экране вновь возникает прямая линия, проходящая на этот раз через другие квадранты. При дальнейшем смещении вновь переменит свое направление и т. д. Таким образом, при помощи фигур, получивших название фигур Лиссажу, можно непосредственно измерить длину звуковой волны в воздухе и по формуле (1) определить скорость звука.
, то на экране вновь возникает прямая линия, проходящая на этот раз через другие квадранты. При дальнейшем смещении вновь переменит свое направление и т. д. Таким образом, при помощи фигур, получивших название фигур Лиссажу, можно непосредственно измерить длину звуковой волны в воздухе и по формуле (1) определить скорость звука.


