Порядок выполнения работы. 1. Измерите длину проволоки ℓ0 линейкой (рулеткой).
1. Измерите длину проволоки ℓ0 линейкой (рулеткой). 2. Определить диаметр проволоки d микрометром не менее чем в пяти местах и найти среднее из всех измерений dср и найдите площадь по сечения S 3. Познакомьтесь с отсчетным микроскопом МИР – 2. 4. Установите длину тубуса микроскопа 160 мм, что соответствует цене деления шкалы микроскопа 0,045 мм. 5. Направьте микроскоп на измерительную метку 6 и получите ее четкое изображение в поле зрения микроскопа. 6. Снимите зависимость удлинения проволоки Δℓ0 от нагрузки при возрастающей и уменьшающейся нагрузках. Результаты исследований занесите в таблицу 1.
Результаты эксперимента.
7. Постройте график координатах Р.(Δℓ0) и убедитесь в совпадении прямых при увеличении и уменьшении нагрузки на проволоку, где P =mg. 8. Вычислите среднее удлинение проволоки Δℓ0 при действии на нее одного груза Р. 9. Определите величину Е. по формуле:
10. Вычислите относительную ошибку полученного результата по формуле:
11. Запишите полученный результат и сделайте выводы.
Задание 2: Определение модуля Юнга из изгиба. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ прибор для исследований упругих свойств стержня, стержень из исследуемого материала, набор грузов штангенциркуль, измерительная линейка.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ В данной работе изучается простейший случай деформации – деформация изгиба. Из рисунка 4 видно, что данная деформация сводится к неоднородным деформациям сжатия и растяжения. Для определения модуля Юнга Е., характеризующего эти деформации, в теории упругости выводиться формула /2/,пользуясь которой можно определить значение E для стержня прямоугольного сечения с помощью легко измеряемых на опыте величин:
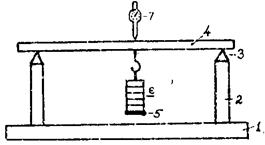
Рис.4 где K= l- стрела прогиба, м F - величина нагрузки; L- расстояние между опорами при м, м; B - ширина стержня, м; H- толщина стержня, м. Формула выведена в предположении, что ребра опорных призм параллельны, а прогибающая сила приложена в середине стержня. Экспериментальная установка /рис.5/ состоит из массивной стальной балки 1 со стойками 2. На концах стоек установлены опорные призмы 3, на которые опирается исследуемый стержень 4.К середине исследуемого стержня крепится держатель с площадкой 5, на которую навешиваются грузы 6.Изгиб стержня определяется с помощью индикатора часового типа 7 или с помощью микрометрического винта с электрической системой индикации.
Рис.5
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. 1. Измерьте линейкой расстояние между ребрами призм L. 2. Определите ширину B и толщину H стержня штангенциркулем. 3. Результаты измерений величин L, B, H занесите в таблицу 1.
Таблица 1. Результаты измерений L, B, H
4. Исследуемый стержень установите на опорные призмы и к ее середине подвесьте площадку для грузов. 5. Приведите в соприкосновение с центром исследуемого стержня измерительный конец индикатора или микрометрического винта и запишите их начальные положения при нулевом значении нагрузки на стержне. 6. Снимите зависимость величины прогиба стержня от величины нагрузки P=mg при увеличении и уменьшении нагрузки. Результаты занесите в таблицу 2. Таблица 2 Результаты измерений
Обозначения в таблице 2: m -массы грузов; n1-показания микрометрического винта или индикатора при увеличении нагрузки до максимальной; n2 -показания при уменьшении нагрузки от максимальной до полной разгрузки стержня; l1 -величина прогиба стержня при увеличении нагрузки; l2 -то же при уменьшении нагрузки; l –полное значение прогиба стержня при грузе P. 7.По данным таблицы 2 постройте график зависимости величины прогиба от величины нагрузки при увеличении и уменьшении нагрузки и сделайте выводы. 8.Определить модуль Юнга E по формуле /2/. 9.Оцените погрешность измерений по формулам:
DE= M*E, Н/м2 10.Запишите полученный результат и сделайте выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ. 1.Какие деформации вы знаете? 2.Сформулируйте закон Гука. 3.Каков физический смысл модуля Юнга? 4.Расскажыте об устройстве экспериментальных установок.
|






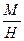
 %;
%;


