Результаты работы и их анализ.
Таблица 3.1-Данные градуировки спектроскопа по спектру ртути.
По данным таблицы 3.1 строим градуировочный график, который представлен на рисунке 3.1. Для получения гладкой кривой воспользуемся интерполяцией экспериментальных точек.
По графику представленному на рисунке 3.1 найдём длины волн спектра атома водорода, результаты занесём в таблицу 3.2. Таблица 3.2-Экспериментальные данные спектра атома водорода.
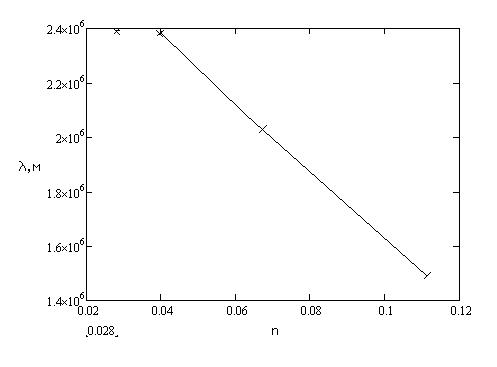
Построим график зависимости 1/ λ = f(1/n2). Он представлен на рисунке 3.2. Прямую строим методом линейной регрессии, при этом не учитываем одну точку, которая, как мы видим, не укладывается на прямой.
Рисунок 3.2 – график зависимости 1/ λ = f(1/n2)
Определим постоянную Ридберга по формуле (2.2). Для этого возьмем точки: 1/ λ = 1,49*10-6 м-1 1/n2= 0,1111 1/ λ = 2,08*10-6 м-1 1/n2= 0,0625 1/ λ = 2,38*10-6 м-1 1/n2= 0,04 1/ λ = 2,39*10-6 м-1 1/n2= 0,0278
R=1,092*107 м-1
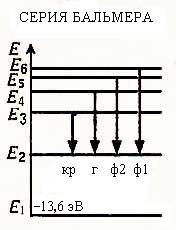
Построим фрагмент энергетического спектра атома водорода:
Заключение В ходе выполнения данной работы был изучен спектр излучения атома водорода. Экспериментально определена постоянная Ридберга, её значение: R = 1,092*107 м-1, при этом табличное значение: R = 1,097 x 107 м-1. А так же построили часть спектра тома водорода.
|
Рисунок 3.1 – Градуировочный график φ(λ)
