Эластикалық тамырдағы қан жүруінің кинетикасы.
Тамыр соғу. Франк моделі Негізгі гемодинамикалық процесс ретінде тамыр соғу толқынының таралуы жатады. Егер жүректен әртүрлі қашықтықтағы нүктелердегі артерия қабырғасының деформациясын тіркейтін болсақ, онда тамыр деформациясы нүктелерге кеш жетеді, яғни тамыр арқылы тамыр соғу толқындары тарайды. Тамырдың жиі соғуы – пульсациялық тербеліс түрінде тарайтындықтан тамыр көлемінде бір-бірімен тығыз байланыстағы қысым және қан айналымының жылдамдығы өзгеріп отырады. Тамыр толқыны – көлем өзгеруінің эластикалық тамыр бойымен таралуына сәйкес бір мезгілде қысым мен сұйық массасының өзгеруіне негізделген процесс. Тамыр толқынының сипаттамасын қарастырайық – тамыр толқынының амплитудасы деп Р0 (х) (тамырлық қысым) тамырдың берілген нүктесіндегі қысымының Max және Min шамаларын айтамыз. Аортаның басындағы нүктеде толқын амплитудасы Р0,max, систоликалық Рс және диастоликалық Рд қысымдарының айырмашылығына тең болады. Р0,max= Рс – Рд (1) Тамыр бойымен тараған тамырлық толқынның амплитудасының өшуі мына теңдеу бойынща анықталады. Р0 (х) = Р0,maх e-βx (2) Мұндағы: β - өшу коэфиценті, ол радиус кеміген сайын өседі. Тамырлық толқынның таралу жылдамдығы тамыр мен қанның қасиетінде байланысты.
Е – тамыр материялының Юнг модулі Һ - тамырдың қалындығы r - тамырдың радиусы
Тәжірибе арқылы өлшенген тамырлық толқынның таралу жылдамдығы Vт = 6-8 м/с бұл қан бөлшектерінің қозғалыс жылдамдығынан Vc = 0,3 - 0,5 м/с 20-30 мәрте көп. Жүрек қарыншасынан қуылып шыққан уақыт ішінде tq = 0,3с (систол уақыты) тамырлық толқын L = Vnt = 2 м ара қашықтыққа тарап үлгіреді, яғни барлық ірі тамырларды аорта және артерияларды толтырып үлгіреді. Тәжірибе жүзінде тамыр толқындарының таралу жылдамдығын өлшеу тамыр мүшелерінің жағдай күйлерін анықтау үшін диагностиканың негізін құрайды Адам есейген сайын Юнг модулі Е-тамыр толқын жылдамдығының өсуіне байланысты 2-3есе өседі. «Тамыр-қан» жүйесінде тамырлық толқынмен қатар-дыбыстық толқындарда тарай алады, олардың жылдамдығы қан бөлшектерінің қозғалыс жылдамдығы мен тамыр соғу толқындарының жылдамдығына қарағанда анағұрлым көп болады. Сонымен ЖҚТ- жүйесінде негізінен 3-процесті бөлуге болады: 1. Қан бөлшектерінің орын ауыстыруы - Vk = 0,5 м/с 2. Тамыр соғу- толқындарының таралуы - VT = 10 м/с 3. Дыбыс толқынының таралуы – Vд = 1500 м/с Cол қарыншадағы қысым (Р) мен көлемдік жылдамдықтың уақыт бойынша өзгеруі 6.3.-суреттен көрініп тұрғандай Р мен Q уақыт бойынша сызықты түрде өзгермейді.
6.3.-сурет. Жүрек тамырының жиырылуы кезіндегі гемодинамикалық көрсеткіштерінің өзгеруі. 1899 ж. неміс физиологы О. Франк теориялық түрде- артериялар систол кезінде қанды жинақтап, диастол кезінде оларды майда тамырлар арқылы денеге итеріп шығаратындығын ашты. Ыңғайлы болу үшін Жүректің сол қарыншасынан- ірі тамыр – майда тамырларға келіп түсетін қан айналымының 2-деңгейін қарастырамыз: 1-ші фаза - Жүректен аортаға – аортаның клапаны ашылғаннан бастап жабылғанға дейін қан келіп тұрады. 6.3.-суреттегі 1-2-3 нүктелер. Жүректен қан түскен сайын ірі тамырлардың қабырғалары кеміп, қанның кейбір бөліктері сонда жиналып кейбір бөліктері майда тамырларға көшеді. 2-ші фаза - Аорталық құлақшажабылғаннан кейін қан ірі тамырлардан майда тамырларға (6.3.-суреттегі 3→11 нүктелер) өтеді. Бұл фаза кезінде бір тамырдың қабырғалары олардың эластикалық серпімділік қасиеттеріне сәйкес бұрынғы қалыптарына қайтып келеді де майда тамырларға айдайды. Бұл кезде сол қарыншаға қан жүректің сол жағын келіп түседі. Франк моделінде мынандай 5 жорамал жасалынады: 1. Барлық ірі тамырлар бір резервуарға біріктірілген оның көлемі қысым шамасына пропорционал. Олар жоғары эластикалық қасиетке ие резервуардың гидровликалық кедергісі ескерілмейді. 2. Микротамырлардың қабырғалары қатты түтікше түрінде қарастырылған (берілген). Қатты түтікшенің гидравликалық кедергісі өте үлкен, майда тамырлардың эластикалығы ескерілмейді. 3. Әр бір тамырлар тобы үшін эластикалығы мен кедергісі уақыт пен кеңестікте тұрақты түрде сақталады. 4. Қан қозғалысының тағайындалуында өтпелі процестерде қарастырылады 5. Жүректің активтілігіне байланысты, сыртқы механизм жұмыс істейді. Ол аорталық клапанды ашып жауып отырады. Осы процестерді сипаттайтын теңдеуді құрастырайық. Резервуардың көлемінің өзгеру жылдамдығы dv/dt –жүректен шығатын Qc қан жылдамдығымен майда тамырларға енетін қан жылдамдығының айрымына тең болады.
Резервуардың көлемінің өзгеруі сызықты түрде қысымның өзгеруіне байланысты болғандықтан. dv = CdP (5) мұндағы С- Қатты түтік бойымен қанның ағуына Пуазейль заңын қолдансақ.
Р – ірі тамырдағы қысым Р соң - қатты түтіктен шыға берістегі қысым. W –майда тамырлардың гидраваликалық кедергісі. Барлық теңдеулерде қысым ретінде Р – нақты қысым мен атмосфералық қысымдардың айрымы алынады. 4,5,6- теңдеулерде салыстырмалы P(t), Q(t), V(t) түрінде шешуге болады
Бұл біртекті сызықты дифференциалдық теңдеу. Бұл теңдеудің шешімі
К- тұрақты коэффициент 2- ші суретте 8 формула бойынша P (t) - ның– Qc (t) үшін есептелген парабола тәріздес қисығы берілген. Qc (t) = - at2 + bt (9)
Qmах - жүректен шығатын қан айналымының максимум мәні
|

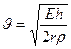 (3)
(3)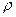 - қаның тығыздығы
- қаның тығыздығы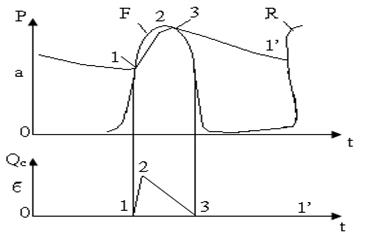
 (4)
(4)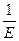 эластикалығы, – қысым мен қөлем арасындағы пропорционалдық коэффициент
эластикалығы, – қысым мен қөлем арасындағы пропорционалдық коэффициент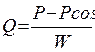 (6)
(6)
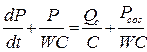 (7)
(7)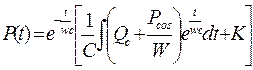 (8)
(8)
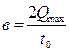 (10)
(10)


