Гемодинамиканың негізгі заңдары
Гемодинамика – грек сөзі – қан – биофизиканың бір тарауы. Мұнда жүрек – тамыр жүйесінде қан қозғалысының себептерін, механизмдерін тексеруге гидродинамика заңдары қолданылады. Адам мен жануарлар организмінде қанның атқаратын қызметі өте зор. Өкпеге барған қан оттегімен өзінің құрамын толтырып алып, оны басқа органдар мен бұлшық еттерге таратады. Клеткалардан қанға кейбір алмасу заттары келіп түседі. Қан оларды бүйрек, өкпе және т.б. мүшелерге жеткізеді. Сонымен қатар, қан таза физикалық қызмет атқарады, ол денедегі жылуды бір жерден 2ші жерге тасымалдайды. Қан негізінен плазма деп аталатын сұйықтан және эритроцит, лейкоцит, тромбоцит деп аталатын клеткалардан тұрады. Түсі қызыл, өте тұтқыр сұйық. Қанда плазма 55-60%, ал қалғандары (эритроцит, лейкоцит, тромбоцит) – 40-45 % болады. Организмді оттегімен қамтамасыз етуде эритроцит үлкен қызмет атқарады. Адам қанынадағы эритроциттің диаметрі шамамен 8 мкм, жылқыныкі – 5,6; сиырдыкі – 5,1 мкм. Адам мен жануарлар қанындығы эритроциттің саны өте көп. Мысалы: Адамның 1 мм3 қанында шамамен 4-5,5 млн. эритроцит болса, жылқыда 8-10 млн, сиырда 6 -7 млн болады. Егер қанға ол ұйып қалмайтын зат қосатын болсақ, онда эритроциттер ауырлық күшінің әсерінен шөгеді. Эритроциттердің осы шөгу жылдамдығын Стокс заңымен анықтауға болады. Эритроциттердің шөгу жылдамдығының өзгеруі (оны РОЭ ден атайды) организмнің сау немесе ауру екендігі туралы мағлұмат береді. Мысалы. Адам ауырған кезде оның РОЭ-сы өседі. Гемодинамика – биомеханиканың бір саласы, ол қан тамырлары арқылы қанның ағу заңдарын зерттейді. Гемодинамиканың негізгі көрсеткіштеріне қан ағымының жылдамдығы мен қан қысымы жатады. Қысым – қанның тамырлардың бірлік ауданына түсіретін күші
Қан айналымының көлемдік және сызықтық жылдамдығын анықтайды. 1) Көлемдік желдамдық деп (Q) құбырдың (тамырдың) берілген ауданы бойынша бірлік уақыт ішінде ағатын сұйықтың көлеміне тең шаманы айтады.
2) Сызықтық жылдамдық деп қан бөлшектерінің бірлік уақыт ішінде жүріп өткен жолын айтады
Сызықтық және көлемдік жылдамдықтар өзара мынандай байланыста болады. Q=VS (4) Сұйық сығылмайтын болғандықтан ( Q=VS=const (5). Бұл ағынның үздіксіздік теңдеуі. Бұл теңдеу сығылмайтын сүйық үшін массаның сақталу заңын өрнектейді. Нақты сұйықтардың құбыр арқылы қозғалысы (ағыны) кезінде потенциалдық энергия ішкі үйкелісті жеңуге кететін жұмысқа жұмсалатын болғандықтан, сұйық ағынының қысымы құбыр бойымен төмендейді. Тұрақты көлденең қимасы бар цилиндрлік құбырдағы стационар ламинарлық ағыс үшін Гаген-Пуазейль теңдеуі (заңы) орындалады.
Бұл теңдеуді 1839 ж. Гаген, 1940 ж. Пуазеиль тағайындаған. Құбырдың гидравликаның кедергісі мына теңдеумен анықталады.
Сонда 6-шы теңдеуді мына түрде жазуға болады.
Пуазейль заңынан шығатын қорытынды қан тамырларындағы қан қысымының азаюы – қан ағымының көлемдік жылдамдығы мен тамырдың радиусына тәуелді болады. Мысалы. Тамыр радиусының 20% - ке азаюы (кемуі) қан қысымының 2 есе төмендеуіне алып келеді. Пуазейль заңының қолдану шегі: 1. Ламинарлық ағын 2) Гомогендік сұйық, 3) Түзу қатты құбырлар, 4) Тітіркену мен қозу көздерінен (ағынның кірген, құбырдың майысқан және диаметрлерінің кішірейген) алшақ орналасқан жерлер. Гидравликалық кедергі - көп мөлшерде тамырдың (құбырдың) радиусына тәуелді болады. Әр түрлі радиусты тамырлар жүйесі үшін радиус қатынастары мынаған тең: Rаорт: Rар: R кап = 3000:500:1 Гидравликалық кедергі Wкап>Wар>Wаорт Қан ағынының сызықтық жылдамдығы. Үздіксіздік теңдеуінен барлық капиллярдың саңлауларының аудандарының қосындысы, аортаның көлденең қимасынан 500 - 600 есе (үлкен) көп болады, яғни Vкап= Капиллярлық жүйеде қанның жай (аз) жылдамдығында клетка мен қан арасында зат алмасу жүреді.
|

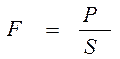 (1).
(1).
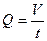 (2)
(2) 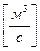
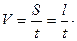 (3)
(3) 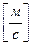
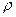 =const) онда құбырдың кез келген көлденең қимасынан бірлік уақыт ішінде бірдей көлемдегі сұйық ағып өтеді.
=const) онда құбырдың кез келген көлденең қимасынан бірлік уақыт ішінде бірдей көлемдегі сұйық ағып өтеді.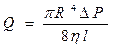 (6)
(6)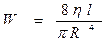 (7)
(7)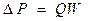 (8)
(8)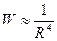 - болғандықтан тамыр жүйелері үшін
- болғандықтан тамыр жүйелері үшін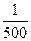 Vаорт
Vаорт 


