ББК 32.973 14 страница
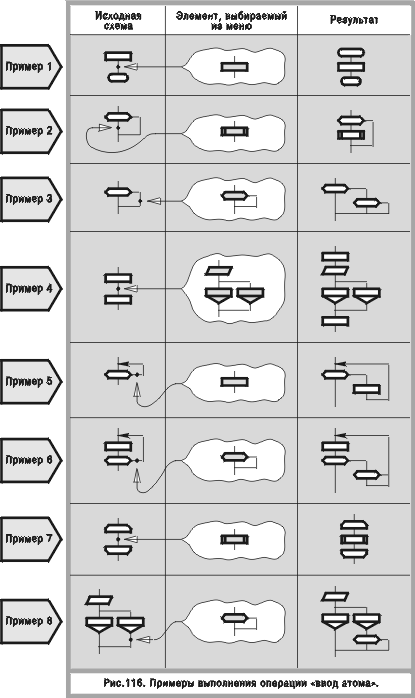
Атомы вставляются не куда попало, а только в разрешенные места, которые называются валентными точками дракон-схемы. Перечень точек включает: ! валентные точки заготовок (отмечены на рис. 115); ! валентные точки макроикон (отмечены на рис. 2); ! входы и выходы атомов. Ввод атома производится так: происходит разрыв соединительной линии в выбранной пользователем валентной точке, после чего в место разрыва вставляется атом, как показано на рис. 116. В реальных дракон-схемах валентные точки не изображаются, а подразумеваются.
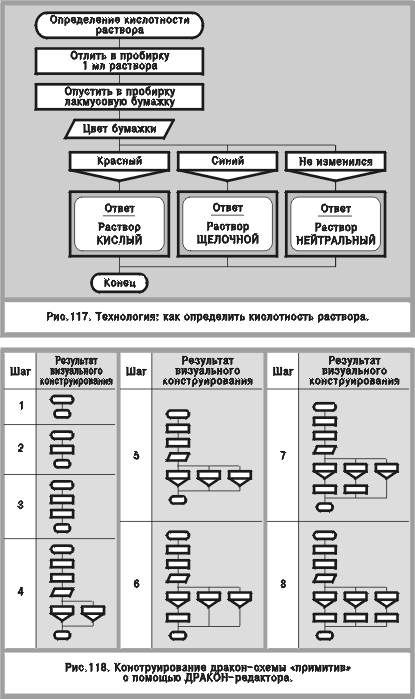
ПРИМЕР ПОСТРОЕНИЯ ДРАКОН-СХЕМЫ Дракон-схема строится на экране компьютера методом “сборки из кубиков”. Чтобы посмотреть, как это делается, нарисуем схему, изображенную на рис. 117. В начале работы пользователь вызывает на экран визуальное меню (рис. 114) и размещает его в удобном для себя месте, например в правом верхнем углу экрана. Остальная часть экрана используется как рабочее поле для построения дракон-схемы. Схема, которую мы хотим построить (рис. 117), — это примитив. Поэтому прежде всего нужно поместить в рабочее поле заготовку-примитив. Для этого на первом шаге графического конструирования пользователь обращается к меню, подводит курсор к макроиконе “заготовка-силуэт”, преобразует ее в заготовку-примитив и копирует последнюю Два следующих шага выполняются аналогично: в дракон-схему вводятся еще одна икона “действие” и макроикона “переключатель” (рис. 118, шаги 3 и 4). Далее следует операция “добавление варианта”, выполняемая без обращения к меню. С ее помощью модифицируется макроикона “переключатель”, к которой добавляется еще одна икона “вариант” (рис. 118, шаг 5). Последующий ход строительства ясен из рис. 118 (шаги 6—8). После того как графический узор (слепыш) дракон-схемы построен, производится заполнение его текстом. Окончательный результат работы редактора показан на рис. 117. ОПЕРАЦИЯ “ПЕРЕСАДКА ЛИАНЫ” Обезьяна, сидевшая на дереве, поймала свисавшую сверху лиану. Однако нижняя часть лианы приросла к стволу и не поддавалась. Обезьяна перегрызла ее зубами, уцепилась за конец и мигом перелетела на соседнее дерево, где намертво привязала лиану к ветке. Нечто подобное умеет делать и ДРАКОН-редактор. Роль верхнего конца лианы играет выход иконы “вопрос” или “вариант”. Лиана — это присоединенная к нему последовательность шампур-блоков или просто соединительная линия. При некоторых условиях (подробно описанных в следующей главе) нижний конец лианы можно оторвать от своего места и присоединить в другую точку дракон-схемы. Такая операция называется пересадка лианы.
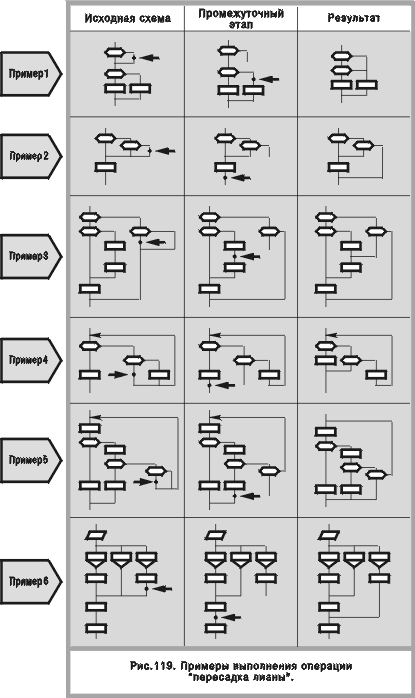
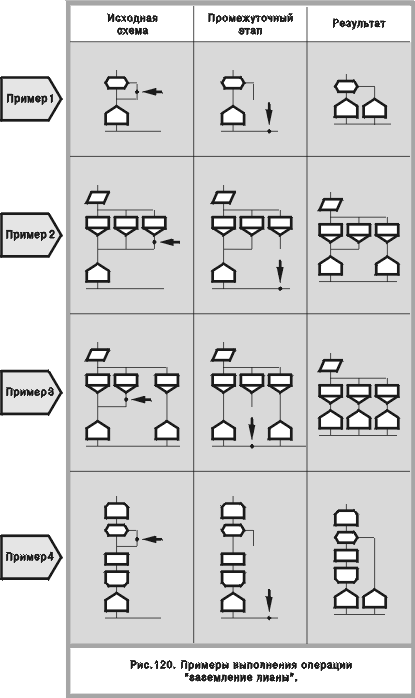
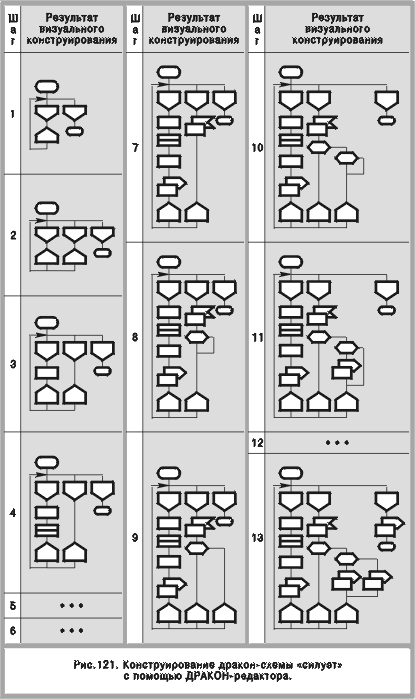
Выполнение этой операции не требует обращения к меню и осуществляется в два этапа. Сначала курсор подводится к нижнему концу лианы, который пользователь желает освободить (рис. 119, левая графа). Но куда его присоединить? Пользователь выбирает желаемую точку и отмечает ее курсором (рис. 119, средняя графа). Результат операции “пересадка лианы” показан на том же рисунке в правой графе. Многие дракон-схемы, представленные в этой книге, построены с помощью пересадки лианы. Укажем некоторые из них: рис. 26 б, 27 б, ОПЕРАЦИЯ “ЗАЗЕМЛЕНИЕ ЛИАНЫ” Функция “пересадка лианы” универсальна в том смысле, что она применима и к примитиву, и к силуэту. В отличие от нее операция заземление лианы относится только к силуэту. Она служит для построения веток, имеющих несколько выходов (многоадресных веток). Для этого необходимо организовать в ветке разветвление (с помощью макроикон “развилка” или “переключатель”), затем оторвать присоединенную к ним лиану от прежнего места и присоединить ее через икону “адрес” к нижней горизонтальной линии силуэта, “заземлить” ее. Операция “заземление лианы” проводится в два этапа без обращения к меню. Первый этап (отрыв нижнего конца лианы от своего места) осуществляется точно так же, как при пересадке лианы (рис. 120, левая графа). На втором этапе пользователь подводит курсор к нижней линии силуэта, указывая точку, куда лиана может дотянуться, не пересекая других линий (рис. 120, средняя графа). Это действие порождает автоматическое появление в нужном месте иконы “адрес”, через которую лиана и присоединяется к нижней линии (рис. 120, правая графа). Заземление лианы использовалось при построении силуэтов с многоадресными ветками, например, на рис. 4, 6 а, 51–54, 84, 88, 89. ПРИМЕР ПОСТРОЕНИЯ Построим визуальную программу, изображенную на рис. 96. На первом шаге конструирования пользователь обращается к меню и вызывает в рабочее поле заготовку-силуэт (рис. 121, шаг 1). На следующем шаге с помощью операции “добавление ветки” (которая выполняется без обращения к меню) он модифицирует заготовку, вставляя в силуэт еще одну ветку (рис. 121, шаг 2). Дальнейший ход строительства ясен из рисунка: в шагах 3—8, 10—13 реализуется операция “ввод атома”, в шаге 9 — “заземление лианы”. Графическое конструирование заканчивается в момент получения желаемого слепыша (рис. 121, шаг 13).
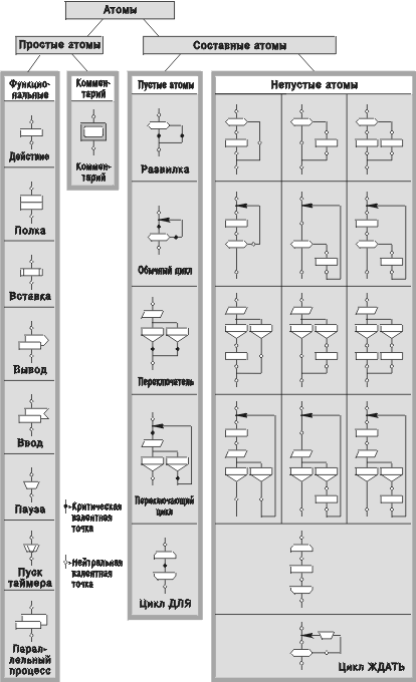
Затем в иконах записываются текстовые операторы, после чего визуальная программа приобретает окончательный вид, показанный на рис. 96. Данная программа может выполняться методом интерпретации или же транслироваться в объектный код. ФОРМИРОВАНИЕ НАДПИСЕЙ “ДА” И “НЕТ” Вернемся к обсуждению рис. 121 и подробнее остановимся на шаге 13, на котором завершается графическое построение дракон-схемы и в качестве результата на экране возникает слепыш. Дело в том, что законченный чертеж-слепыш, сформированный при реальной работе ДРАКОН-редактора, имеет отличие от абстрактной дракон-схемы, изображенной на рис. 97. Последняя полностью лишена текста (не содержит ни одной буквы или цифры), а построенный редактором слепыш возле каждой иконы “вопрос” обязательно имеет надписи “да” и “нет”. Эти надписи появляются на дракон-схеме всякий раз, когда из меню вызывается элемент с иконой “вопрос” в ходе операции “ввод атома”. Согласно алгоритму этой операции редактор пишет “да” у нижнего выхода иконы “вопрос” и “нет” — у правого. Чтобы пользователь в случае необходимости мог поменять их местами, в редакторе предусмотрена операция “да-нет”. Применение последней к конкретной иконе “вопрос” приводит к тому, что слова “да” и “нет” у ее выходов меняются местами (при этом все остальные элементы дракон-схемы остаются на своих местах). ВЫВОДЫ 1. Хотя общее число икон и макроикон языка ДРАКОН равно 45, для построения любой дракон-схемы достаточно иметь небольшое меню, содержащее всего 18 графоэлементов. 2. Визуальное меню существенно облегчает работу пользователя — оно дает возможность конструировать дракон-схему методом “сборки из кубиков”. Для этого служит операция “ввод атома”, позволяющая доставать “кубики” из меню и укладывать их в проектируемую дракон-схему. 3. Другие операции (“пересадка лианы”, “заземление лианы” и т. д.) разрешают вносить в схему логические детали и “украшения”, расширяющие ее функциональные возможности и улучшающие эргономическое качество. 4. В алгоритмах ДРАКОН-редактора реализован полный набор правил визуального синтаксиса, что освобождает пользователя от необходимости подробно запоминать синтаксические правила. 5. ДРАКОН-редактор создает только правильно построенные схемы и исключает возможность появления запрещенных схем. Отсюда вытекает, что при работе с ДРАКОН-редактором ошибки визуального синтаксиса принципиально невозможны. Г Л А В А 15 Описание визуального синтаксиса ...наглядность, говоря обыденным языком, в один день научает нас с большей легкостью и прочностью тому, чему не могут научить правила, повторяемые хотя бы тысячу раз, так как собственное наблюдение... идет здесь рука об руку с теоретическим определением. Галилео Галилей ОБЩИЕ ПОНЯТИЯ Тезис 1. Иконы — визуальные буквы, образующие визуальный алфавит языка ДРАКОН, представленные на рис. 1. Тезис 2. Заготовка-примитив и заготовка-силуэт — фигуры, показанные на рис. 115. Предварительный тезис 3. Примитив — фигура, полученная путем преобразования заготовки-примитив за конечное число шагов с помощью фиксированного набора операций (перечисленных ниже в тезисе 36). Предварительный тезис 4. Силуэт — фигура, полученная путем преобразования заготовки-силуэт за конечное число шагов с помощью фиксированного набора операций (перечисленных ниже в тезисе 37). Тезис 5. Дракон-схема — общее понятие для обозначения примитива и силуэта. ШАМПУР-БЛОК Тезис 6. Шампур-блок — часть дракон-схемы, имеющая один вход сверху и один выход снизу, содержащая одну или несколько икон, причем: ! вход и выход лежат на одной вертикали, через которую проходит путь от входа к выходу; ! через каждую икону, входящую в состав шампур-блока, проходит хотя бы один путь от входа к выходу; ! в состав шампур-блока могут входить любые иконы за исключением следующих: заголовок, конец, формальные параметры, петля силуэта. Тезис 7. Главная вертикаль шампур-блока — вертикаль, соединяющая его вход и выход. Остальные вертикали, если они есть, находятся правее главной. Все вертикали шампур-блока ориентированы сверху вниз, кроме цепей, используемых для организации петли цикла. ОПЕРАЦИЯ “ВВОД АТОМА” Тезис 8. Атомы — фигуры, изображенные на рис. 122. Эти фигуры используются в операции “ввод атома”. Любой атом является шампур-блоком. Тезис 9. Валентная точка — точка, принадлежащая заготовке или дракон-схеме, в которой разрешается произвести разрыв соединительной линии, чтобы в место разрыв вставить атом с помощью операции “ввод атома”. Тезис 10. Ввод атома — преобразование заготовки или дракон-схемы, выполняемое следующим образом: производится разрыв соединительной линии в валентной точке и в это место вставляется атом, как показано на рис. 116. Дополнительные сведения об атомах Тезис 11. Атомы делятся на простые и составные. Простой атом состоит из одной иконы, составной содержит не менее двух (рис. 122). Тезис 12. Функциональный атом — простой атом, не являющийся пустым оператором. Таковы все простые атомы, кроме комментария. Тезис 13. Составные атомы бывают пустые и непустые. В непустом есть хотя бы один функциональный атом. В пустом нет ни одного. Тезис 14. В полностью законченной дракон-схеме не должно быть ни одного пустого атома (так как последний эквивалентен пустому оператору). Пустые атомы разрешается использовать на всех этапах построения дракон-схемы, кроме заключительного. Критические и нейтральные точки Тезис 15. Валентные точки делятся на нейтральные и критические. Тезис 16. Точка называется нейтральной, если применение операции “ввод атома” к данной точке является возможным, но не обязательным. В отличие от нее критическая точка требует обязательного ввода атома. Тезис 17. Валентные точки находятся в заготовках и атомах. Они показаны на рис. 115 и 122, где нейтральные точки обозначены светлыми кружками, критические — жирными точками.
Тезис 18. Если в фигуре (заготовке или атоме) одна критическая точка, ввод атома обязательно производится именно в нее; при этом критическая точка уничтожается. Если фигура имеет две критические точки, обязательный ввод атома делается только в одну из них; при этом критическая точка, в которую произведен ввод, уничтожается, а другая критическая точка нейтрализуется, т. е. становится нейтральной. Тезис 19. Полная совокупность критических точек охватывает: ! критические точки в пустых атомах; ! одну критическую точку в заготовке-примитив; ! одну критическую точку в заготовке-силуэт. Тезис 20. Полная совокупность нейтральных точек охватывает: ! входные и выходные точки атомов; ! две внутренние точки в атоме “цикл ЖДАТЬ”; ! одну точку в заготовке-силуэт; ! точки, полученные в результате нейтрализации критических точек. Правила использования операции “ввод атома” Тезис 21. Операция “ввод атома” применяется для ввода только простых и пустых атомов, а также цикла ЖДАТЬ. Ввод непустого атома осуществляется в два этапа; сначала вводится пустой атом, затем в его критическую точку вводится функциональный атом. П о я с н е н и е. Ввод пустого атома — очень удобный строительный прием. Он позволяет обеспечить богатство и разнообразие создаваемых дракон-схем и используемых в них конфигураций. Среди последних особую роль играет так называемая “матрешка”. Тезис 22. Матрешка — фигура, полученная путем ввода пустого атома в критическую точку пустого атома, а также путем многократного вложения пустых и непустых атомов друг в друга (рис. 123). Тезис 23. Матрешка бывает пустой (если все содержащиеся в ней атомы пустые), частично пустой (если в ней есть как пустые, так и непустые атомы) и непустой (если все ее атомы непустые). См. рис. 124—126. П о я с н е н и е. После того как пользователь эффективно использовал пустые атомы для придания дракон-схеме желаемой конфигурации, он должен убрать их из схемы. Тезис 24. Чтобы устранить пустые атомы из дракон-схемы, есть два способа: ! превратить пустой атом в непустой; ! преобразовать пустой атом в пустую матрешку, затем превратить ее в непустую. Тезис 25. Устранение из дракон-схемы пустых атомов автоматически приводит к уничтожению всех критических точек.
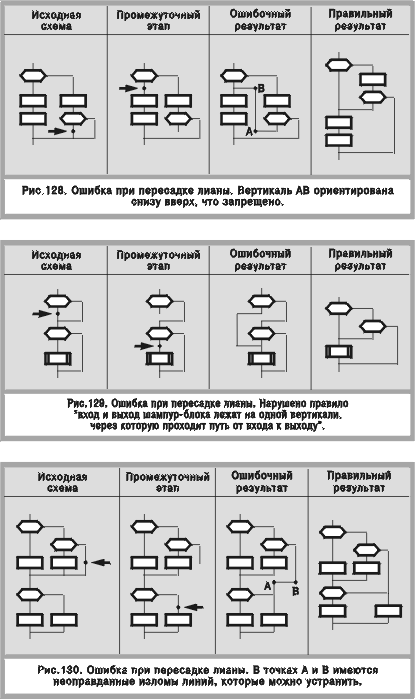
ОПЕРАЦИИ С ЛИАНОЙ Тезис 26. Лиана — часть дракон-схемы, имеющая один вход и один выход, именуемые “началом лианы” и “концом лианы” соответственно. Началом лианы может быть любой выход икон “вопрос” и “вариант”, если он (выход) не является петлей цикла. Концом лианы считается точка слияния, в которой нижняя часть лианы соединяется с другой линией (концом лианы не может быть неразветвленный вход иконы). Тезис 27. Лиана может быть нагруженной (если она содержит иконы) и ненагруженной (если это просто линия). Пересадка лианы Тезис 28. Пересадка лианы — преобразование дракон-схемы, выполняемое за четыре шага. Шаг 1. Производится отрыв конца лианы от точки присоединения (рис. 119). Шаг 2. Конец лианы с помощью вертикальных и горизонтальных линий присоединяется к любой валентной точке, куда лиана может дотянуться без пересечения с другими линиями (рис. 119). При этом запрещается: ! формировать второй вход в ветку (ошибка “сиамские близнецы” — см. рис. 127); ! образовывать новый цикл; ! создавать второй вход в цикл. Однако разрешается строить новый путь из середины обычного цикла к единственному входу в этот цикл, создавая визуальный эквивалент оператора continue языка СИ (см. рис. 90, пример 7, а также рис. 41). Шаг 3. Производится эквивалентное преобразование топологии дракон-схемы, чтобы лиане не пришлось загибаться наверх (рис. 128) Шаг 4. Устраняются неоправданные изломы линий (рис. 130). Заземление лианы Тезис 29. Заземление лианы — преобразование дракон-схемы, выполняемое за четыре шага. Шаг 1. Производится отрыв конца лианы от точки присоединения (рис. 120). Шаг 2. Конец лианы с помощью вертикальной линии присоединяется к любой точке нижней горизонтальной линии силуэта, куда он может дотянуться, не пересекая другие линии. Шаг 3. Производится разрыв линии в нижней части лианы и в место разрыва вставляется икона “адрес” (рис. 120). Шаг 4. Устраняются неоправданные изломы линий.
ПРОЧИЕ ОПЕРАЦИИ Тезис 30. Боковое присоединение — преобразование дракон-схемы, с помощью которого в схему добавляются иконы “синхронизатор” или “формальные параметры”. Икона “синхронизатор” размещается слева от другой иконы и соединяется с ней горизонтальным отростком. Перечень икон, к которым осуществляется боковое присоединение синхронизатора, показан на рис. 2 (п. 8—20). Икона “формальные параметры” размещается справа от иконы “заголовок” и соединяется с ней горизонтальным отростком, как показано на рис. 2 (п. 1). Тезис 31. Добавление варианта — преобразование дракон-схемы, с помощью которого в атом “переключатель” добавляется еще одна икона “вариант”. Число добавлений не более 14, так что максимальное число вариантов в переключателе равно 16. Тезис 32. Добавление ветки — преобразование силуэта, в который добавляется еще одна ветка. Число добавлений не более 14, так что максимальное число веток в силуэте равно 16. Тезис 33. Удаление последней ветки — преобразование силуэта, при котором удаляется крайняя правая ветка. Этот прием используется при описании бесконечного параллельного процесса, как показано в примерах на рис. 88 и 89. Тезис 34. Удаление конца примитива — преобразование примитива, при котором удаляется икона “конец”. Это необходимо для описания бесконечного параллельного процесса. Тезис 35. Дополнительный вход — преобразование силуэта, с помощью которого добавляется еще одна икона “заголовок”, которая размещается над любой иконой “имя ветки” (кроме левой) и соединяется с ней вертикальным отростком. При этом на верхней горизонтальной линии силуэта рисуют направленную вправо стрелку, как показано в примере на рис. 84 справа. О г р а н и ч е н и е. При наличии веточного цикла запрещается присоединять дополнительный заголовок к середине веточного цикла. ОСНОВНЫЕ РЕЗУЛЬТАТЫ Тезис 36. Любая правильно построенная дракон-схема “примитив” является результатом преобразования заготовки-примитив с помощью конечного числа операций: ввод атома, пересадка лианы, добавление варианта, боковое присоединение, удаление конца примитива. Тезис 37. Любая правильно построенная дракон-схема “силуэт” является результатом преобразования заготовки-силуэт с помощью конечного числа операций: ввод атома, добавление ветки, пересадка лианы, заземление лианы, добавление варианта, боковое присоединение, удаление последней ветки, дополнительный вход. П о я с н е н и е. Тезисы 36 и 37 могут рассматриваться как окончательные определения понятий “примитив” и “силуэт”. ВЫВОДЫ 1. Изложенные выше 37 тезисов (вместе с рисунками, на которые они ссылаются) дают однозначное описание визуального синтаксиса, которое при желании можно изложить строгим математическим языком. 2. Это описание является достаточным для построения ДРАКОН-редактора, способного решить две задачи. Во-первых, нарисовать (в соответствии с указаниями пользователя) любую абстрактную дракон-схему, принадлежащую множеству правильно построенных (удовлетворяющих требованиям визуального синтаксиса) дракон-схем. Во-вторых, создать в памяти компьютера формальное описание построенной схемы, пригодное (после заполнения икон надлежащими текстовыми операторами) для трансляции в объектные коды или для выполнения программы в режиме интерпретации.
Г Л А В А 16 Визуальное структурное Наше мышление основано в первую очередь на зрительном восприятии. Вадим Глезер ПОСТАНОВКА ПРОБЛЕМЫ Попробуем включить воображаемый “боковой прожектор” и взглянуть на проблему под другим углом зрения. Существует некоторое, причем весьма глубокое, хотя и не всегда очевидное сходство между изложенными выше идеями и концепцией структурного программирования. Исходя из этого, введем термин “визуальное структурное программирование” и определим его как набор правил, совпадающий с визуальным синтаксисом языка ДРАКОН. В концентрированном виде эти правила изложены в гл. 15. Чтобы отграничить теоретические аспекты визуального структурного программирования от второстепенных деталей, нам понадобится термин “шампур-метод”. Впрочем, иногда выражения “шампур-метод” и “визуальное структурное программирование” будут использоваться как синонимы. Размышляя над проблемой, автор пришел к следующим предварительным выводам или, лучше сказать, предположениям. ! Несмотря на наличие целого ряда общих признаков, текстовое и визуальное структурное программирование — существенно разные вещи. ! Традиционное (текстовое) структурное программирование является, по-видимому, наилучшим решением соответствующей задачи для традиционного (текстового) программирования. ! Для визуального программирования подобное утверждение неправомерно. Можно, конечно, тупо перенести правила текстового структурного программирования на визуальный случай. Но это не будет хорошим решением. ! Чтобы разработать эффективный метод структуризации для визуального варианта, необходимо, взяв за основу правила текстового структурного программирования, значительно модифицировать их. ! Принципы структуризации, положенные в основу визуального синтаксиса языка ДРАКОН, являются искомым решением. В данной главе сделана попытка обосновать заявленные выводы. ИСТОРИЧЕСКАЯ СПРАВКА Согласно классической теореме Бома и Джакопини, всякая реальная программа может быть построена из функциональных блоков (действий) и двух конструкций: цикла и дихотомического выбора (развилки) [1]. Эдсгер Дейкстра обогатил и усилил эту идею, предложив отказаться от оператора безусловного перехода goto и ограничиться тремя управляющими конструкциями: последовательность, цикл, выбор [2]. Дональд Кнут подверг критике тезис Дейкстры о полном исключении goto, продемонстрировав случаи, где goto полезен. В итоге возникла плодотворная дискуссия, строго говоря, не завершенная до сих пор, в ходе которой выявились четыре варианта мнений (табл. 4). Таблица 4
Вариант 1 описывает ортодоксальную позицию Дейкстры, согласно которой оператор goto имеет “гибельные последствия” и поэтому “должен быть исключен из всех языков программирования высокого уровня”. Исходя из этого были разработаны языки без goto: PDL [3], BLISS и др. Вариант 2 отражает мнение ранних критиков Дейкстры, позиция которых выражается словами: “использование оператора goto может оказаться уместным в лучших структурированных программах”; “всегда были примеры программ, которые не содержат goto и аккуратно расположены лесенкой в соответствии с уровнем вложенности операторов, но совершенно непонятны, и были другие программы, содержащие goto и все же совершенно понятные”. Поэтому нужно “избегать использования goto всюду, где это возможно, но не ценой ясности программы” [4]. Как известно, полемика по goto “растревожила осиное гнездо” и всколыхнула “весь программистский мир”. Варианты 1 и 2 выражают крайние позиции участников дискуссии, между которыми, как казалось вначале, компромисс невозможен. Однако ситуация изменилась с изобретением и широким распространением заменителей goto, примерами которых являются: в языке СИ — операторы break, continue, return и функция еxit (), в языке МОДУЛА-2 — операторы RETURN, EXIT, процедура HALT и т. д. Заменители — особый инструмент, который существенно отличается как от трех структурных управляющих конструкций, так и 1) не требуя меток, заменители исключают ошибки, вызванные путаницей с метками; 2) каждый заменитель может передать управление не куда угодно (как goto), а в одну-единственную точку, однозначно определяемую ключевым словом заменителя и его местом в тексте. В результате множество точек, куда разрешен переход, сокращается на порядок, что также предотвращает ошибки. Вариант 3 описывает языки СИ, АДА и др., где имеются заменители и на всякий случай сохраняется goto.
|