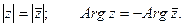Методические указания к проведению лекционного занятия
Тема № 1.9. Комплексные числа. План: 1. Основные понятия и определения. 2. Действия с комплексными числами. 3. Показательная форма комплексного числа. Основные понятия и определения
Опр.: Комплексным числом z называется выражение
При этом число a называется действительной частью числа z (a = Re z), а b - мнимой частью (b = Im z). Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
Опр.: Числа
Опр.: Два комплексных числа
Замечание: Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.
Геометрическое представление комплексного числа: Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел. Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.
Таким образом, на оси Ох располагаются действительные числа, а на оси Оу – чисто мнимые. С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.
Тригонометрическая форма числа: Из геометрических соображений видно, что
Такая форма записи называется тригонометрической формой записи комплексного числа. При этом величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа.
Из геометрических соображений видно:
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.
|

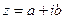 , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
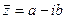 называются комплексно – сопряженными.
называются комплексно – сопряженными.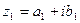 и
и 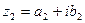 называются равными, если соответственно равны их действительные и мнимые части:
называются равными, если соответственно равны их действительные и мнимые части:
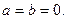

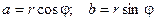 . Тогда комплексное число можно представить в виде:
. Тогда комплексное число можно представить в виде:

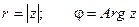 .
.