Перестановки с повторениями
Кофе)D (чай)D (кофе)D (чай)D
И теперь правильно считаем по правильной формуле:
Перестановками из n элементов называются размещения из этих n элементов по n (Перестановки - частный случай размещений). Число перестановок без повторений (n различных элементов) вычисляется по формуле:
Число перестановок c повторениями (k различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 +… + mk = n, где n - общее количество элементов) вычисляется по формуле:
Пример. Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза? Решение. 1. Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА. По формуле (3.3) получаем: 2. Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА. По формуле (3.4) получаем: Перестановки с повторениями Всякое размещение с повторениями, в котором элемент
в которой данные элементы Теорема. Число различных перестановок с повторениями из элементов
Доказательство. Если мы будем считать все
Задача. Дано
Вопрос №9 Вывод формул числа всех разбиений множества на части определённых мощностей (упорядоченные и неупорядоченные). Неупорядоченное разбиение n -элементного множества X — это любое семейство { X 1, X 2,…, X k}, где 1 ≤ k ≤n; X1, X2,…,Xk - непустые попарно непересекающиеся подмножества множества X, объединение которых равно X. Называем такое разбиение неупорядоченным, так как семейство — это неупорядоченная совокупность. Упорядоченным разбиением конечного множества X с n-элементами называется любой кортеж вида <X1, X2,…,Xk>, где 1 ≤k ≤ n; X1, X2,…,Xk - непустые попарно непересекающиеся, подмножества множества X, объединение которых равно X. Называем такое разбиение упорядоченным, так как элементы кортежа упорядочены. Вопрос №10, 11. Свойства чисел сочетаний Свойства чисел: 1. 2. 3. 4. 5.
Числа С(n, к) возникают как коэффициенты при раскрытии скобок в биноме (а + b)n. Например,
Эта формула называется биномом Ньютона. Ровно поэтому коэффициенты С(n, к) часто называют биномиальными коэффициентами. Биномиальные коэффициенты полезно выстроить в так называемый треугольник Паскаля
Вопрос №12. Задача о числе счастливых билетов. Само решение требует достаточно большого числа вычислений, однако они не очень сложные. Важно понять, как их сократить. Найдем Сначала докажем, что Далее нам понадобится число способов представления целого неотрицательного числа Число способов
Теперь перейдем к
Для
Число билетов, у которых сумма первых трех цифр равна сумме последних трех цифр и равна Осталось найти общую сумму:
Итак, всего есть
Группы, кольца, поля Вопрос №13. Группа, кольцо, поле. Примеры числовых групп, колец, полей. Множество 1. Операция 2. В 3. для каждого элемента Примеры групп: · Все целые, все рациональные, все действительные и все комплексные числа являются группами относительно операции сложения чисел, играющего роль групповой операции умножения; · Все рациональные, все действительные и все комплексные числа, исключая число 0, являются группами относительно операции умножения чисел. Если операция Множество 1. Относительно операции сложения множество · операция сложения коммутативна: · операция сложения ассоциативна: · существует нулевой элемент · для каждого элемента 2. Операция умножения во множестве 3. Операции сложения и умножения связаны законами дистрибутивности.
Если операция умножения коммутативна: Примеры колец при обычных операциях сложения и умножения кольцом является: 1. Множество целых чисел; 2. Множество рациональных чисел; 3. Множество действительных чисел; 4. Множество рациональных чисел; 5. Множество, состоящее лишь из одного числа 0; 6. Множество четных чисел и вообще множество целых чисел, кратных некоторому числу n; 7. Множество комплексных чисел a + bi с целыми a и b (так называемое кольцо целых комплексных чисел). Множество 1. 2. Для каждого элемента Поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел. Примеры полей: 1. Множество комплексных чисел a + bi с любыми рациональными a, b; 2. Множество всех рациональных функций с действительными коэффициентами от одного или нескольких переменных; 3. Множество из двух элементов, которые обозначим через 0 и 1, при следующем определении операций:
Вопрос №14, 15. Действие группы на множестве, орбита элемента, подгруппа, теорема Лагранжа о порядке подгруппы. Группа 1. 2. Для любых 3. Для любого Действие группы: · Действие группы на себя. Пусть · Действие сопряжением. Пусть
Орбитой элемента x ∈ X под действием G называется множество Gx = {gx | g ∈ G}. Количество элементов в данной орбите называется длиной орбиты (в разных орбитах может быть разное количество элементов). Любые две орбиты либо не пересекаются, либо совпадают. Таким образом, мно- жество X разбивается в дизъюнктное объединение орбит Подгруппа ― подмножество Подмножество · содержит произведение любых двух элементов из · содержит вместе со всяким своим элементом В случае конечных и, вообще, периодических групп проверка условия 2 является излишней. Теорема Лагранжа: В конечных группах порядок любой подгруппы делит порядок группы Формула (лемма) Бернсайда о числе орбит.
Вопрос №16, 17. Задача о числе раскрасок вершин правильного многогранника (куба, тетраэдра, октаэдра). Сколькими способами можно раскрасить вершины куба в три цвета (например, красный, синий и зеленый)? На первый взгляд может показаться, что задача совсем простая. Поскольку каждую из восьми вершин куба можно раскрасить тремя способами, причем независимо от того, как раскрашены другие вершины, то множество всех вершин куба можно раскрасить При этом полученный ответ можно интерпретировать следующим образом: можно так раскрасить Ситуация существенно меняется, если мы откажемся от предположения о том, что кубы жестко закреплены, так как по-разному окрашенные кубы можно повернуть так, что в новом положении их окраски совпадут (рис. 33).
Рис. 33 Естественно считать, что два куба раскрашены одинаково, если их раскраски совпадают после некоторого вращения одного из кубов в пространстве. Будем говорить, что такие раскраски кубов геометрически неотличимы. Поэтому естественным уточнением задачи о раскраске является следующая задача: Сколькими геометрически различными способами можно раскрасить вершины куба в три цвета. Переформулируем теперь эту задачу так, чтобы стала понятной ее связь с леммой Бернсайда. Пусть М — множество всевозможных по-разному раскрашенных кубов одного размера, положение которых в пространстве фиксировано, То, что два куба Считая вершины кубов занумерованными числами 1,2, 3, 4, 5, 6, 7, 8, раскраску каждого из 38 кубов можно однозначно охарактеризовать «словом» из 8 букв, каждая из которых есть либо к, либо с, либо з. То, что i-я буква слова равна к (или с, или з), означает; что i-я вершина при выбранной нумерации окрашена в красный цвет (или в сцний, или в зеленый соответственно). Например, для куббв, изображенных на рис. 33, имеем соответственно последовательности Для того чтобы применить лемму Бернсайда, необходимо определить число неподвижных точек каждой перестановки из G. Последовательность букв Поэтому сначала мы опишем разложения в произведение циклов для всех перестановок из группы G вращений куба. а) Вокруг каждой из трех осей, соединяющих центры противоположных граней, имеется три нетождественных вращения. Им соответствуют перестановки
б) Вокруг каждой из четырех диагоналей, т. е. осей, соединяющих противоположные вершины куба, имеется по два нетривиальных вращения. Им соответствуют перестановки
в) Вокруг каждой из шести осей, соединяющих середины противоположных ребер, имеется одно нетривиальное вращение. Им соответствуют перестановки
Вместе с тождественной получаем 24 перестановки. Итак, в группе G вращений куба имеется
Перестановка первого типа имеет
Таким образом, число геометрически различимых способов раскраски вершин куба в три цвета равно 333. Вопрос №18. Кольца и поля вычетов, решение уравнений в кольцах и полях вычетов.
|

 Где n - количество всех элементов, n1 - количество элементов первого типа, n2 - количествово элементов второго типа и т.п.
Где n - количество всех элементов, n1 - количество элементов первого типа, n2 - количествово элементов второго типа и т.п. Вот всего-то получается комбинаций.
Вот всего-то получается комбинаций.

 наборов.
наборов. наборов.
наборов. повторяется
повторяется  раз, элемент
раз, элемент  повторяется
повторяется  раз и т.д. элемент
раз и т.д. элемент  повторяется
повторяется  раз, где
раз, где 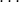 ,
, 
 повторяются соответственно
повторяются соответственно  , в которых элементы
, в которых элементы  раз, равно
раз, равно
 элементов перестановки с повторениями различными, то всего различных вариантов перестановок
элементов перестановки с повторениями различными, то всего различных вариантов перестановок  . Однако среди этих перестановок не все различны. В самом деле, все элементы
. Однако среди этих перестановок не все различны. В самом деле, все элементы  ,
,  способами. Следовательно, число различных перестановок с повторениями равно
способами. Следовательно, число различных перестановок с повторениями равно различных предметов. Сколькими способами можно разбить эти предметы на 3 группы так, чтобы первая группа содержала
различных предметов. Сколькими способами можно разбить эти предметы на 3 группы так, чтобы первая группа содержала  предметов, вторая
предметов, вторая  предметов, а третья
предметов, а третья  предметов?
предметов?
 , бином Ньютона.
, бином Ньютона.

 ;
; ;
;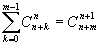 , (m1);
, (m1);


 — число билетов, у которых сумма первых трех цифр равна сумме трех последних цифр и равна
— число билетов, у которых сумма первых трех цифр равна сумме трех последних цифр и равна  . Ясно, что
. Ясно, что  (три
(три  (три “девятки’’).
(три “девятки’’). . В самом деле, каждой последовательности из трех десятичных цифр с суммой цифр
. В самом деле, каждой последовательности из трех десятичных цифр с суммой цифр  можно поставить в соответствие последовательность из трех десятичных цифр с суммой цифр
можно поставить в соответствие последовательность из трех десятичных цифр с суммой цифр  следующим образом: каждую цифру
следующим образом: каждую цифру  в исходной последовательности заменим на цифру
в исходной последовательности заменим на цифру  . Тем самым, каждой последовательности из трех десятичных цифр с суммой цифр
. Тем самым, каждой последовательности из трех десятичных цифр с суммой цифр  до
до  столько же, сколько последовательностей с суммой цифр
столько же, сколько последовательностей с суммой цифр  в виде суммы трех целых неотрицательных слагаемых. Это можно сделать
в виде суммы трех целых неотрицательных слагаемых. Это можно сделать  способами. Действительно, число способов равно числу сочетаний с повторениями из
способами. Действительно, число способов равно числу сочетаний с повторениями из  (или иначе, разбиваем
(или иначе, разбиваем  элемента, из которых нужно выбрать
элемента, из которых нужно выбрать  нуля, см. сочетания с повторениями).
нуля, см. сочетания с повторениями). можно вычислить по полученной формуле:
можно вычислить по полученной формуле: :
:  (впрочем, это и так очевидно,
(впрочем, это и так очевидно,  , иначе никак),
, иначе никак), :
:  ,
, :
:  ,
, :
: 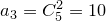 ,
, :
:  ,
, :
:  ,
, :
:  ,
, :
: 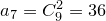 ,
, :
:  ,
, :
:  .
. . Здесь все немного сложнее, потому что цифры
. Здесь все немного сложнее, потому что цифры  не существует, и нам нужно из всех способов разбиения числа
не существует, и нам нужно из всех способов разбиения числа  ). Получаем (с учетом того, что слагаемое
). Получаем (с учетом того, что слагаемое  :
:  .
. поступаем точно так же. Сначала находим число способов представить
поступаем точно так же. Сначала находим число способов представить  в виде суммы трех целых неотрицательных слагаемых — оно равно
в виде суммы трех целых неотрицательных слагаемых — оно равно  , а затем вычитаем те способы, в которых одно из слагаемых больше либо равно десяти — их всего
, а затем вычитаем те способы, в которых одно из слагаемых больше либо равно десяти — их всего  . Итак,
. Итак, :
:  ,
, :
:  ,
, :
:  .
. (независимо от способа выбора первых трех цифр с суммой
(независимо от способа выбора первых трех цифр с суммой 
 .
. “счастливых’’ билета.
“счастливых’’ билета. с алгебраической операцией
с алгебраической операцией  называется группой, если выполняются следующие условия:
называется группой, если выполняются следующие условия: ;
; ;
; существует обратный ему элемент
существует обратный ему элемент  .
. , на котором заданы две операции — сложение
, на котором заданы две операции — сложение  и умножение
и умножение  , называется кольцом, если выполняются следующие условия:
, называется кольцом, если выполняются следующие условия: ;
;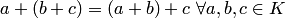 ;
; ;
; существует противоположный ему элемент
существует противоположный ему элемент  ;
; , то кольцо называется коммутативным, в противном случае кольцо называется некоммутативным. Если для операции умножения существует единичный элемент
, то кольцо называется коммутативным, в противном случае кольцо называется некоммутативным. Если для операции умножения существует единичный элемент  , то говорят, что кольцо
, то говорят, что кольцо  , на котором заданы две операции: сложение
, на котором заданы две операции: сложение  ;
; , отличного от нулевого
, отличного от нулевого  , существует обратный элемент
, существует обратный элемент  .
. действует на
действует на  , если любых
, если любых 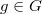 и
и  определено действие элемента
определено действие элемента  на элемент
на элемент  (обозначаемое
(обозначаемое  ), обладающее следующими свойствами:
), обладающее следующими свойствами: ,
, выполнено
выполнено  ,
, .
. и множество
и множество  . Зададим отображение
. Зададим отображение  , такое что
, такое что  . Тогда все свойства из определения выполнятся вследствие соответствующих свойств группы. Таким образом группа
. Тогда все свойства из определения выполнятся вследствие соответствующих свойств группы. Таким образом группа  . Все свойства из определения выполнены, следовательно группа
. Все свойства из определения выполнены, следовательно группа  группы
группы  , само являющееся группой относительно операции, определяющей
, само являющееся группой относительно операции, определяющей  обратный к нему элемент
обратный к нему элемент  .
. эквивалентными, если
эквивалентными, если  для некоторого
для некоторого 

 . Где
. Где  — количество стабилизаторов для элемента
— количество стабилизаторов для элемента  .
.
 .
Следовательно для доказательства леммы необходимо и достаточно доказать следующее равенство:
.
Следовательно для доказательства леммы необходимо и достаточно доказать следующее равенство:  Рассмотрим правую часть равенства:
Рассмотрим правую часть равенства: 




 Заметим, что
Заметим, что 

 Следовательно:
Следовательно:

 .
Очевидно, что
.
Очевидно, что  Тогда получим:
Тогда получим:
 Откуда следует, что
Откуда следует, что
 ч.т.д.
ч.т.д.

 различными способами. Однако при таком подходе к решению задачи молчаливо предполагается, что мы умеем различать вершины куба перед окраской, т. е., скажем, куб жестко закреплен или его вершины занумерованы.
различными способами. Однако при таком подходе к решению задачи молчаливо предполагается, что мы умеем различать вершины куба перед окраской, т. е., скажем, куб жестко закреплен или его вершины занумерованы. абсолютно одинаковых, жестко закрепленных кубов, что все они будут различаться. Для
абсолютно одинаковых, жестко закрепленных кубов, что все они будут различаться. Для  кубов этого сделать уже нельзя.
кубов этого сделать уже нельзя.
 , G — группа всех вращений куба, состоящая из 24 перестановок. Группа G естественным образом определяет группу перестановок на множестве М. Именно: если а
, G — группа всех вращений куба, состоящая из 24 перестановок. Группа G естественным образом определяет группу перестановок на множестве М. Именно: если а  — некоторое вращение, то каждому кубу из М можно сопоставить некоторый, вообще говоря, другой куб, который получается из первого при вращении а. Это соответствие является, очевидно, перестановкой на множестве
— некоторое вращение, то каждому кубу из М можно сопоставить некоторый, вообще говоря, другой куб, который получается из первого при вращении а. Это соответствие является, очевидно, перестановкой на множестве  которую будем обозначать а. Группу всех таких перестановок множества М, определяемых перестановками из G, мы будем обозначать G. Ясно, что
которую будем обозначать а. Группу всех таких перестановок множества М, определяемых перестановками из G, мы будем обозначать G. Ясно, что 
 из М раскрашены геометрически одинаково, означает, что один из них можно перевести вращением в такое положение, в котором они неразличимы. Иными словами, существует такая перестановка
из М раскрашены геометрически одинаково, означает, что один из них можно перевести вращением в такое положение, в котором они неразличимы. Иными словами, существует такая перестановка  что
что  содержатся в одной орбите группы G, действующей на множестве М. Таким образом, для того чтобы определить число геометрически различимых способов раскраски вершин куба, нужно найти количество орбит группы G на множестве М.
содержатся в одной орбите группы G, действующей на множестве М. Таким образом, для того чтобы определить число геометрически различимых способов раскраски вершин куба, нужно найти количество орбит группы G на множестве М. . Перестановки из группы G переставляют такие последовательности. Например, если
. Перестановки из группы G переставляют такие последовательности. Например, если  то перестановка а слово
то перестановка а слово  переводит в
переводит в  , слово ссззсскк переводит в
, слово ссззсскк переводит в  слова
слова  оставляет неизменными и т. д. Выписать всю таблицу значений для перестановки а затруднительно, поскольку она состоит из
оставляет неизменными и т. д. Выписать всю таблицу значений для перестановки а затруднительно, поскольку она состоит из  строк!
строк! будет неподвижной для перестановки
будет неподвижной для перестановки  тогда и только тогда, когда при разложении соответствующей перестановки
тогда и только тогда, когда при разложении соответствующей перестановки  в произведение "Циклов вершины куба, номера которых входят
в произведение "Циклов вершины куба, номера которых входят  один и тот же цикл, окрашены одним цветом. Например, если
один и тот же цикл, окрашены одним цветом. Например, если  , то неподвижными относительно а будут слова, составленные целиком из одной буквы, и слова, составленные из двух разных букв, причем одна из них стоит на первых четырех местах в слове, а вторая — из четырех последующих. Поэтому имеется 9 неподвижных точек перестановки
, то неподвижными относительно а будут слова, составленные целиком из одной буквы, и слова, составленные из двух разных букв, причем одна из них стоит на первых четырех местах в слове, а вторая — из четырех последующих. Поэтому имеется 9 неподвижных точек перестановки  на множестве М. Уже на этом примере видно, что подсчет числа неподвижных точек перестановок из G сильно упрощается, если извесгны разложения в произведение циклов соответствующих перестановок из G. Если перестановка
на множестве М. Уже на этом примере видно, что подсчет числа неподвижных точек перестановок из G сильно упрощается, если извесгны разложения в произведение циклов соответствующих перестановок из G. Если перестановка  разложена в произведение
разложена в произведение  циклов, то число ее неподвижных точек равно
циклов, то число ее неподвижных точек равно 




 неподвижных точек, любая из перестановок второго типа
неподвижных точек, любая из перестановок второго типа  третьего и четвертого типов —
третьего и четвертого типов —  неподвижных точек. Поэтому согласно лемме Бернсайда имеем
неподвижных точек. Поэтому согласно лемме Бернсайда имеем



