Методы получения полиномов Жегалкина.1. Метод равносильных преобразований. Используется для функций, заданных формулой. Метод состоит в выполнении следующих действий. 1) В формуле все функции, кроме суммы Жегалкина и эквиваленции, выражаются через отрицание, конъюнкцию и дизъюнкцию. Эквиваленция заменяется отрицанием операции 2) Дизъюнкция исключается с помощью закона Моргана: 3) Отрицание исключается с помощью свойства суммы Жегалкина: 4) Раскрываются скобки, приводятся подобные с помощью законов:
Пример. 2. Метод неопределенных коэффициентов. Используется для функций, заданных таблицей. Метод состоит в том, что сначала записывается полином Жегалкина для заданной функции в общем виде с неопределенными коэффициентами, затем эти коэффициенты определяются на основе таблицы значений функции от конъюнкции наименьшего ранга к конъюнкциям больших рангов. Пример. Пусть функция задана таблицей 2.14. Запишем полином Жегалкина для f: f (
f (0,0) = f (1,0) = Аналогично, f (0,1) = f (1,1) =
Теперь можно записать выражение (2.5) с определенными коэффициентами: f ( Теорема. Любая функция алгебры логики представима в виде полинома Жегалкина единственным образом с точностью до порядка следования слагаемых.
|
: 
.
.
.
, 
, 
, 
.
= 
= 
= 
= 
= 
= 
.
, 
) = 
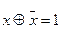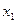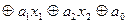(2.5)
, 
)
·0 
·0 
=1 (Значение f (0,0) = 1 выбирается из таблицы).
