Постановка задачи. Постановка задачи: известны статистические свойства входного случайного сигнала Хвх(t), то есть известна n-мерная плотность вероятности при n
Постановка задачи: известны статистические свойства входного случайного сигнала Хвх(t), то есть известна n-мерная плотность вероятности при n, стремящемся к бесконечности, известны характеристики цепи. Надо найти n-мерную плотность вероятности выходного сигнала Хвых(t) при n, стремящемся к бесконечности. Любую нелинейную цепь можно представить в виде совокупности нелинейного элемента (НЭ) и линейного фильтра.
С точки зрения прохождения случайного сигнала нелинейная РЭЦ содержит два узла с противоположными свойствами: 1) Линейный фильтр – очень трудно, а в общем случае невозможно, найти закон распределения случайного сигнала на выходе линейного фильтра, зато легко находятся энергетический спектр, АКФ и неслучайные числовые характеристики. 2) Нелинейный элемент – ниже будет показано, что довольно просто на выходе НЭ находится закон распределения, зато трудно найти АКФ и энергетический спектр. Следовательно, в общем случае задача прохождения случайного сигнала через нелинейную РЭЦ не имеет решения. Поддаются решению лишь частные задачи.
§2. Преобразование одномерного закона распределения случайного сигнала нелинейным безинерционным элементом.
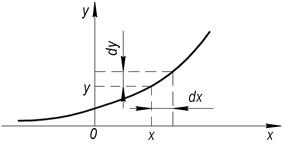
Постановка задачи: известны одномерный закон распределения W(x) случайного сигнала X(t) и характеристика НЭ y=y(x). Требуется найти одномерный закон распределения W(y) случайного сигнала Y(t). В математике подобная задача формулируется как нахождение закона распределения функционально преобразованной случайной величины. При решении этой задачи возможны три случая: 1) Обратная зависимость x=x(y) существует и однозначна, то есть каждому значению y соответствует единственное и вполне определенное значение х.
dx, dy – бесконечно малые приращения. Вероятность попадания у в интервал от у до у+dy равна вероятности попадания х в интервал от х до х+dx.
2) Обратная зависимость х=х(у) существует, но не однозначна, то есть каждому значению у соответствуют несколько вполне определенных значений х.
Вероятность попадания у в интервал от у до у+dy равна сумме вероятностей попадания х в соответствующие интервалы:
В общем случае, когда число значений х равно n:
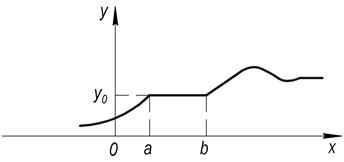
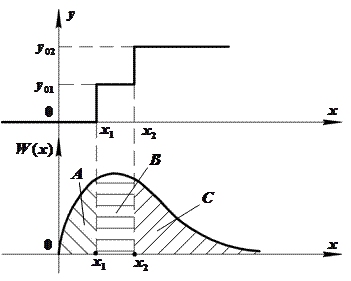
3) Для некоторых значений у обратная зависимость х=х(у) не существует. Эти значения у будем называть особыми точками. Пример:
Во всех точках у, кроме у0, W(y) находится либо по формуле (1), либо (2). Для особой точки y=y0:
Примеры: 1) X(t) – гауссовский случайный сигнал с нулевым матожиданием и дисперсией
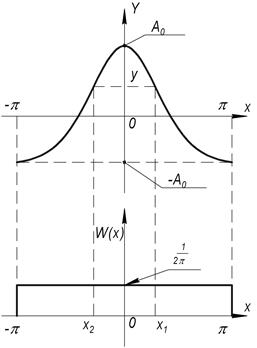
2) X(t) – случайный сигнал с равномерным распределением. Характеристика нелинейного элемента:
Равномерный закон распределения.
3) X(t) – нормальный случайный сигнал
Характеристика нелинейного элемента
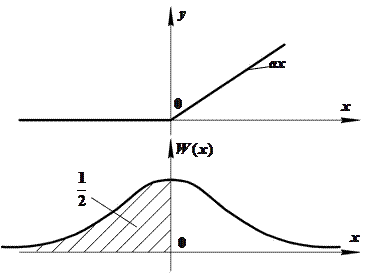
Выделим три области значений ─
4)
Характеристика нелинейного элемента – ступенчатая.
Показать, что
|



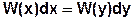
 (1) – решение задачи.
(1) – решение задачи.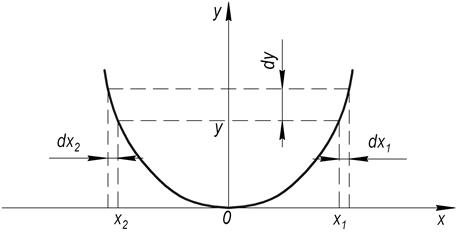
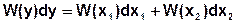
 (2)
(2)
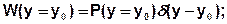 (3)
(3)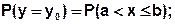
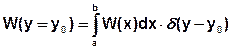
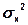 .
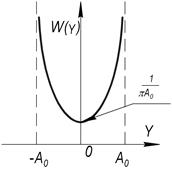
.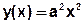 - квадратичная зависимость.
- квадратичная зависимость.

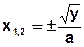

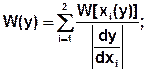
 ,
, 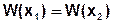
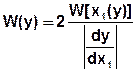
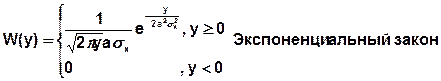

 ,
, 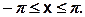
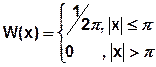 ,
, 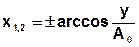
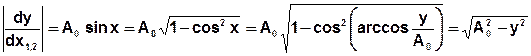
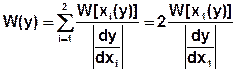
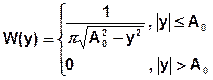
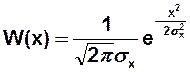
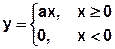
 :
: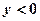 :
: 
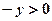 :
: 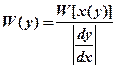
 ;
; 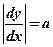
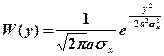 – гауссовский закон распределения
– гауссовский закон распределения :
:
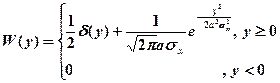

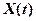 - случайный сигнал с релеевским законом распределения;
- случайный сигнал с релеевским законом распределения;
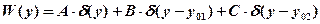 .
.


