Понятие случайного сигнала (СС) и применение для его описания законов распределения и неслучайных числовых характеристик закона распределения.
Понятие случайного сигнала (СС) и применение для его описания законов распределения и неслучайных числовых характеристик закона распределения.
Колебание Х(t) называется случайным сигналом, если его значения в любой момент времени являются случайными величинами Х(ti). Хi=Х(ti) – одномерная случайная величина Если генератор случайного колебания включить на время Т и записать результат х(t), то этот результат принято называть– реализацией СС. Реализация СС – это детерминированный сигнал. Если многократно повторить этот эксперимент, то получится ансамбль реализаций { хк(t) }.
Случайную величину Полное статистическое (вероятностное) описание одномерной случайной величины (СВ) Х(t1) дает одномерный закон распределения СВ. Имеются две разновидности одномерного закона распределения. 1) Интегральный закон распределения (функция распределения)
Значения функции распределения можно найти по ансамблю реализаций:
N – полное число реализаций l – число реализаций, удовлетворяющих условию Х(t1)≤x
Свойства функции распределения: - безразмерная. - неубывающая. - - -
2) Дифференциальный закон распределения (плотность вероятности).
Свойства плотности вероятности:
- размерность [1/x] - W(x)≥0 - свойство нормировки - Пример:
Заштрихованная площадь характеризует вероятность попадания СВ в интервал от a до b.
В общем случае одномерный закон распределения зависит от того, в какой точке проведено сечение, т.е. одномерный закон распределения – функция времени. Кроме одномерного закона распределения для описания случайных величин можно использовать неслучайные числовые характеристики одномерного закона распределения (моменты распределения). Неслучайные числовые характеристики делятся на: 1) Начальные моменты распределения. - начальный момент первого порядка (математическое ожидание СВ) – это среднее значение СВ. Усреднение проводиться по ансамблю реализаций и обозначается
- начальный момент второго порядка – это среднее значение квадрата СВ.
- начальный момент k-порядка – среднее значение СВ в степени k.
2) Центральные моменты распределения – начальные моменты от центрированной СВ:
Второй центральный момент
В общем случае неслучайные числовые характеристики зависят от момента времени, в который проведено сечение, т.е. mx(t),
Знание одномерных законов распределения в различных сечениях СС не дает полного описания СС даже если число сечений стремится к бесконечности, так как одномерный закон распределения не содержит информации о взаимосвязи значений СВ в разных сечениях. Для более полного описания СС необходимо рассматривать совокупность сечений СС как n-мерную случайную величину {X1,X2,…,Xn}. Для описания n-мерной случайной величины применяют n-мерный закон распределения. W(x1 x2, …xn) – n-мерная плотность вероятности. Свойства n-мерной плотности. - нормировка
- зная n-мерную плотность можно найти одномерную плотность в любом сечении
- статистическая независимость сечений. Два сечения называются статистически независимыми, если двумерная плотность равна произведению одномерных плотностей.
Если все сечения статически независимы, то
Заметим, что n-мерный закон распределения дает полное статистическое описание СС при n→∞.
|


 можно назвать сечением случайного сигнала
можно назвать сечением случайного сигнала  в момент времени
в момент времени  .
. - вероятность того, что СВ не превышает некоторого значения х.
- вероятность того, что СВ не превышает некоторого значения х. (при больших N)
(при больших N)



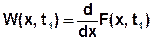


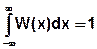


 .
.






 - функции времени.
- функции времени.






