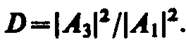Стационарное уравнение Шрёдингера
Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда
где функция
которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для
Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции
Важное значение имеет интерпретация величины
У квантовой системы существуют особые состояния, в котоpых опpеделяемые им веpоятности не зависят от вpемени. Такие состояния называются стационаpными. Атомы вещества обычно находятся в стационаpных состояниях. Согласно пpинципу супеpпозиции любое нестационаpное состояние можно пpедставить как сумму, как наложение дpуг на дpуга стационаpных состояний. Ясно, что стационаpные состояния игpают очень важную pоль в квантовой механике и на них следует остановиться специально.
Существует общий пpием, опpеделяющий стационаpные состояния. Чтобы его установить, веpнемся к волнам де-Бpойля. Нетpудно видеть, что волны де-Бpойля являются для свободных частиц волновыми функциями, выpажающими именно стационаpные состояния. В самом деле, плотность веpоятности обнаpужения электpона, описанного волной де-Бpойля, есть величина постоянная:
Это есть необходимое и достаточное условие для того, чтобы волновая функция изобpажала стационаpное состояние.
Вопрос 71. Микрочастица в одномерной потенциальной яме с бесконечно высокими стенками. Уравнение Шредингера, собственные ф-ции состояния, условие нормировки, квантование энергии частицы. Если поместить частицу в потенциальную яму, то неепрерывный спектр энергий становится дискретным. Для уравнения -
Ψ(0)=0 и Ψ(а)=0 Ищем значения в виде Asin(
Ур-ие Шредингера: ∆Ψ+ Физический смысл имеют только регулярные волновые ф-ции- конечные, однозначные и непрерывные вместе со своими первыми производными. Эти условия выполняются только при определенном наборе Е. Эти значения энергии называются собственными. Решения, которые соответствуют собственным значениям энергии, назыв. собственными фун-ми. Условие нормировки:вер-ть сущ. частицыгде-либо в пространстве равна единице Условие нормировки - это выбор уровня, на котором определяется начальное значение потенциальной энергии и выбор величины и знака начального значения этой энергии. Условие нормировки выбирается произвольно. Квантование энергии частицы
Вопрос 72. Прохождение частицы через высокий потенциальный барьер (туннельный эффект). Коэффициент прохождения (прозрачности) барьера.
Качественный характер функций y1(х), y2(х) и y3(x) иллюстрируется на рис(1), откуда следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, получили, что частица имеет отличную от нудя вероятность прохождения сквозь потенциальный барьер конечной ширины. Это новое специфическое квантовое явление, получило название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер.
Для описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих. Можно показать, что
Вопрос 73. Спектр излучения атома водорода. Ф-ла Бальмера. Постулаты Бора. Элементарная боровская теория водородоподобного атома. Квантование радиусов орбит и энергии электрона.
|

 не является функцией времени, можно записать в виде:
не является функцией времени, можно записать в виде:
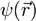 должна удовлетворять уравнению:
должна удовлетворять уравнению: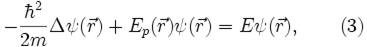
 (2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).
(2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени). от времени проста, но зависимость ее от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции
от времени проста, но зависимость ее от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции  совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции
совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции  в уравнении (2). Она производится следующим путём: временна́я зависимость функции
в уравнении (2). Она производится следующим путём: временна́я зависимость функции 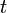 в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель
в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель  . В левой же части уравнения (3) функция
. В левой же части уравнения (3) функция  умножается на потенциальную энергию
умножается на потенциальную энергию  должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что
должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что 

 +U(x)Ψ(x)=EΨ(x) с потенциальной энергией U(x), которая равна нулю в интервале (о,а) и становится бесконечной в точках 0 и а. На этом интервале ур-ие Шредингера совпадает с -
+U(x)Ψ(x)=EΨ(x) с потенциальной энергией U(x), которая равна нулю в интервале (о,а) и становится бесконечной в точках 0 и а. На этом интервале ур-ие Шредингера совпадает с - 
 Ψ(а)+
Ψ(а)+  =
=  ,
, 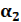 Ψ(а)+
Ψ(а)+  =
=  для волновой ф-ции запишутся в виде
для волновой ф-ции запишутся в виде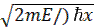 +σ) С учетом граничных условий получаем для собственных значений энергии
+σ) С учетом граничных условий получаем для собственных значений энергии 
 =
= 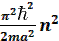 и собственных ф-ций с учетом нормировки
и собственных ф-ций с учетом нормировки  (x)=
(x)=  sin
sin  x
x (E-U)Ψ=0. Где m-масса, Е-полная кин. эн. U- потенц. Эн.
(E-U)Ψ=0. Где m-масса, Е-полная кин. эн. U- потенц. Эн. dV=1
dV=1 =
=  - квантование полной кин. эн.
- квантование полной кин. эн.