Эффект комптона
Комптон исследовал упругое рассеяние коротковолнового рентгеновского излучения на свободных (или слабо связанных с атомами) электронах вещества. Открытый им эффект увеличения длины волны рассеянного излучения, названный впоследствии эффектом Комптона, не укладывается в рамки волновой теории, согласно которой длина волны излучения не должна изменяться при рассеянии. Согласно волновой теории, электрон под действием периодического поля световой волны совершает вынужденные колебания на частоте волны и поэтому излучает рассеянные волны той же частоты.
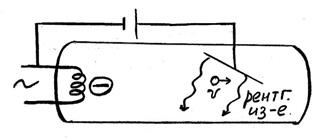
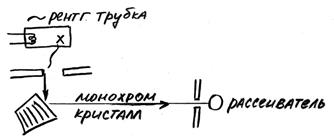
Монохроматическое рентгеновское излучение с длиной волны λ0, исходящее из рентгеновской трубки R, проходит через свинцовые диафрагмы и в виде узкого пучка направляется на рассеивающее вещество-мишень P (графит, алюминий). Излучение, рассеянное под некоторым углом θ, анализируется с помощью спектрографа рентгеновских лучей S, в котором роль дифракционной решетки играет кристалл K, закрепленный на поворотном столике. Опыт показал, что в рассеянном излучении наблюдается увеличение длины волны Δλ, зависящее от угла рассеяния θ:
где Λ = 2,43·10–3 нм – так называемая комптоновская длина волны, не зависящая от свойств рассеивающего вещества. Вопрос 67. Корпускулярно-волновой дуализм материи. Волновые св-ва микрочастиц. Гипотеза де Бройля. Волны де Бройля. Опыты Девиссона – Джермера по дифракции электронов. Корпускала – частица. Дуализм – двузначность, двусторонность. В связи с тем, что в одних явлениях свет проявляет себя как волна (интерференция, дифракция), в других – как частица, де-Бройль распосронил корпускулярно-волновой дуализм на частицы с массой покоя
Идея опытов Девиссона – Джермера: если пучок электронов обладает волновыми св-вами, то можно ожидать, не зная механизма отражения волн, что их отражение от кристалла будет иметь такой же интерференционный характер, как у рентгеновских лучей. В серии опытов для обнаружения дифракционных максимумов измерялись ускоряющее напряжение электронов и одновременно положение счётчика отражённых электронов D. В опыте использовался монокристалл никеля (кубический, рис.).
Вычислив, длину дебройлевской волны λ по ф-лам де-Бройля и (1) при V=54 [B] получили значения 0,167 [нм] и 165 [нм] – разница настолько мала, что опыт признан док-вом гипотезы де-Бройля.
Показатель преломления дебройлероской волны:
Вопрос 68. Соотношение неопределённостей Гейзенберга, их применение и следствия. В классич. физике частица описывается исчерпывающе динамическими параметрами: координатой, импульсом, моментом импульса, энергией и др. В ней нет никаких ограничений на точность опр-ия этих параметров. Однако реальное поведение микрочастиц показывает, что существует принципиальный предел точности, с которой подобные переменные могут быть указаны и измерены. Анализ причин существования этого предела – принцип неопределённости: параметры не могут быть всегда сколь угодно точно определимы. Кол-венные соотношения, выражающие этот принцип в конкречтных случаях, наз-ют соотношениями неопределённостей. Два самых важных: - соотношение ограничивает точность одновременного измерения координат и соответствующих проекций импульса частицы. Для проекции, например, на Ох: смысл: если положение частицы, например, по Ох известно с неопределённостью - устанавливает неопределённость измерения энергии ΔЕ за данный пр-к времени Δt: смысл: для измерения энергии с погрешностю ΔЕ необх. время, не меньшее Пример: возьмём пылинку массой m=1 [мг], с помощью микроскопа определили её положение с погрешностью Δх=10-7 [м]. Найти неопредёлённость скорости шарика.
Следствия: 1) невозможно состояние, в котором частица находилась бы в состоянии покоя; 2) при рассмотрении движения квантового объекта необх. во многих случаях отказаться от самого понятия классической траектории 3) часто теряет смысл деление полной энергии Е частицы (как квантового объекта) на потенциальную U и кинетическую К (U зависит от координат, К – от импульса. эти же динамические переменные не могут иметь одновременно определённого значения).
Вопрос 69. Волновая ф-ция, ее назначение и физический смысл. Пл-ть вер-ти обнаружения частицы. Требования (условия) для волновой ф-ции. Принцип суперпозиции состояний Волнова́я фу́нкция (пси-функция) — функция, используемая в квантовой механике для описания чистого состояния квантовомеханической системы, имеющей протяжённость в пространстве. Физ.Смысл: Единственной характеристикой волновой функции, непосредственное измерение которой возможно — это квадрат её модуля
Требуемые условия для волновой ф-ции:ф-ция должна быть 1) конечной 2) Непрерывной 3) Монотонной 4) Однозначной 5) Дифференцируемой Принцип суперпозиции состояний: Ква́нтовая суперпози́ция (когерентная суперпозиция) — это суперпозиция состояний, которые не могут быть реализованы одновременно с классической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции.
Если функции
Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными Вопрос 70. Стационарные состояния и стационарное ур-ие Шредингера. Собственные значения энергии и собственные ф-ции.
|

 : если с такой частицей связана волна (не электромагнитная), то волна будет распостраняться в направлении вектора скорости частицы.
: если с такой частицей связана волна (не электромагнитная), то волна будет распостраняться в направлении вектора скорости частицы. Гипотеза де-Бройля: для всех частиц длина волны:
Гипотеза де-Бройля: для всех частиц длина волны:  (ф-ла де-Бройля), где h - постоянная Планка, λ – дебройлевская длина волны частицы с импульсом p.
(ф-ла де-Бройля), где h - постоянная Планка, λ – дебройлевская длина волны частицы с импульсом p. Если кристалл повернуть вокруг вертикальной оси в положение, соответствующее рисунку, то в этом положении сошлифованная пов-ть покрыта правильными рядами атомов, ┴ к пл-ти рисунка. Детектор помещали в пл-ти рисунка, меняя угол θ. При угле θ=50 и ускоряющем напряжении V наблюдался особенно отчётливо максимум отражённых электронов (рис.). Этот максимум можно истолковать как интерференционный максимум первого порядка от плоской дифракционной решётки с периодом:
Если кристалл повернуть вокруг вертикальной оси в положение, соответствующее рисунку, то в этом положении сошлифованная пов-ть покрыта правильными рядами атомов, ┴ к пл-ти рисунка. Детектор помещали в пл-ти рисунка, меняя угол θ. При угле θ=50 и ускоряющем напряжении V наблюдался особенно отчётливо максимум отражённых электронов (рис.). Этот максимум можно истолковать как интерференционный максимум первого порядка от плоской дифракционной решётки с периодом: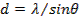 (1)
(1)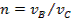 , где
, где  - фазовая скорость волны в вакууме,
- фазовая скорость волны в вакууме,  – в среде (кристалле).
– в среде (кристалле).
 Фазовая скорость дебройлевских волн:
Фазовая скорость дебройлевских волн:  , где
, где  - кинетическая энергия частицы,
- кинетическая энергия частицы, 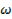 - частота волны,
- частота волны, 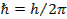 , m – масса частицы.
, m – масса частицы.
 , то в тот же момент проекцию импульса можно измерить только с неопределённостью
, то в тот же момент проекцию импульса можно измерить только с неопределённостью 

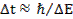
 =>
=>  [м/с]
[м/с] , смыслом которой является плотность вероятности
, смыслом которой является плотность вероятности  обнаружить систему в положении, описываемом координатами
обнаружить систему в положении, описываемом координатами  в момент времени
в момент времени  :
: .
.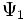 и
и  являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция,
являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция, 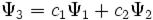 , также описывает какое-то состояние данной системы.
, также описывает какое-то состояние данной системы.


