Закон Ома для замкнутой цепи.
Количественный закон, связывающий эти величины, представляет закон Ома для замкнутой цепи: ток в цепи, содержащей источник тока, прямо пропорционален э. д. с. источника и обратно пропорционален полному сопротивлению цепи.
Если обозначить э. д. с. источника через ξ, его внутреннее сопротивление через r, сопротивление внешней цепи через R, а ток через I, то закон Ома представится следующей формулой:
(80.1) Мы видим, что ток, который способен дать источник, зависит не только от э. д. с. источника и сопротивления внешней цепи, но еще и от внутреннего сопротивления. Сказанное относится, конечно, не только к гальваническим элементам, но и к любым источникам тока, например к аккумуляторам или генераторам постоянного тока.
Вопрос 20. Закон Джоуля-Ленца в интегральной и дифференциальной форме.
n Закон Джоуля-Ленца в интегральной форме В случае, когда проводник с током неподвижен в пространстве и в нем не происходит химических превращений, работа постоянного тока, определяется как: A = U∙I∙t (21) где I∙t = q – заряд, прошедший за время t через каждое сечение проводника, U – напряжение, приложенное к концам проводника. Причем для однородного участка цепи эта работа равна A = (φ;1 – φ;2)∙ q, а для неоднородного участка цепи - A = (φ;1 – φ;2)∙ q + E 12 ∙q. Работа (21) затрачивается на увеличение внутренней энергии проводника, в результате чего он – нагревается. Принято говорить, что при протекании тока в проводнике выделяется тепло в количестве Q = U∙I∙t, а заменив по закону Ома напряжение U = I∙R, приходим к интегральной форме закона Джоуля-Ленца: Q = R∙I 2 ∙t
n Закон Джоуля-Ленца в дифференциальной форме Для характеристики локального тепловыделения используется понятие удельной тепловой мощности тока ([Дж/м3.с]). Выделим в проводнике элементарный цилиндрический объем.
где dV = dS∙dl.
Разделив последнее выражение на (dV∙dt), определим количество тепла, выделяющегося в единице объема в единицу времени: Qуд. = r∙j 2 или Qуд. = j2/σ (24) Выражения (24) являются дифференциальной формой закона Джоуля-Ленца. Это наиболее общая форма записи данного закона – работает для любых проводников вне зависимости от их формы, однородности и природы сил, возбуждающих электрический ток.
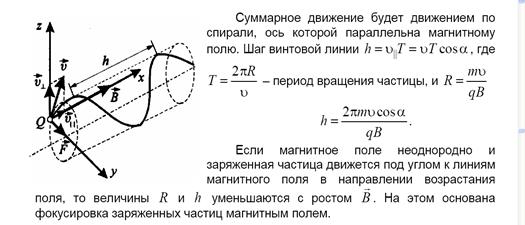
Вопрос 21. Обобщенная сила Лоренца. Движение заряженной частицы в однородных электрическом и магнитном полях. Определение удельного заряда частицы. Магнитное поле – это силовое поле, которое создается движущимися заряженными частицами и проявляет себя действием силы на движущийся заряд.(сила Лоренца) Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Магнитное поле – векторное поле, хар-ся вектором
Движение частицы с зарядом q и массой m в однородном постоянном электрическом поле напряженностью Движение заряженных частиц в магнитном поле. Удельный заряд частицы - физическая величина, равная отношению заряда частицы к ее массе. Экспериментальное определение удельных зарядов частиц производится с помощью масс-спектрографов и основано на отклонении заряженных частиц в электрическом и магнитном поле. Вопрос 22. Магнитное поле тока в вакууме. Закон Био-Савара. Принцип суперпозиции для магнитных полей и его применение для расчета поле кругового тока. Магнитное поле – это силовое поле, которое создается движущимися заряженными частицами и проявляет себя действием силы на движущийся заряд.(сила Лоренца)
Магнитное поле создается токами.
|
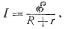
В случае переменной во времени силы тока джоулево тепло рассчитывается по формуле:
Согласно закону Джоуля-Ленца в форме (23) за время dt выделяется элемен-тарное тепло δQ = R∙I 2 ∙dt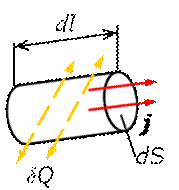
Если на носители тока действуют только электрические силы, то (24) можно переписать как = j∙E = σ∙E 2.
, Тл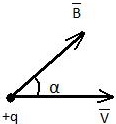
→ 
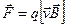. Напряженность поля в этом случае не зависит ни от координат, ни от времени. Следовательно, на заряженную частицу со стороны поля действует постоянная сила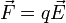 
, которая сообщает частице постоянное ускорение 
- силовая хар-ка.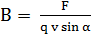 
_|_ 
