Поле на границе раздела двух однородных диэлектриков. Условия преломлённости векторов E и D.
- ротор - Условия, которым должны удовлетворять - -
- Условия справедливы и для границы раздела диэлектрика с вакуумом. Условия справедливы как для электростатического поля, так и для полей, изменяющихся во времени. З-н преломления линий электрического смещения:
где
Вопрос 14. Электроемкость. Емкость плоского, цилиндрического и сферического конденсаторов.
n Емкость проводников Рассмотрим некоторый уединенный проводник, т. е. проводник, удаленный от других проводников, тел (могут быть диэлектрики) и зарядов. Сообщенный проводнику заряд q распределяется по его поверхности так, чтобы везде внутри проводника было поле Е = 0, а на поверхности Е = Е п. Поэтому, если уже заряженному проводнику дополнительно сообщить еще заряд q, то последний должен распределиться по проводнику аналогичным образом, как и первый заряд q. Из подобия распределений различных порций заряда следует, что отношение плотностей заряда в двух произвольных точках поверхности проводника при любом q – будет постоянным. Отсюда следует, что потенциал уединенного проводника φ; пропорционален находящемуся на нем заряду q (это также подтверждается экспериментом).
Простейший конденсатор состоит из двух проводни-ков (обкладок), расположенных на малом расстоянии друг от друга. Чтобы внешние тела не влияли на емкость конденсатора, его обкладкам придают такую форму и так располагают относительно друг друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было сосредоточено практически полностью внутри конденса-тора. Последнее означает: линии вектора Е начинаются на одной обкладке и заканчиваются на другой, а заряды на обкладках равны по модулю: +q = |- q |.
Емкость конденсатора зависит от его геометрии (размеров и формы обкладок), от величины зазора между обкладками (d) и от диэлектрической проница-емости (ε;) среды, заполняющей конденсатор, т. е. можно записать: С = f (форм-фактор; d; ε;). Пример 1: Емкость плоского конденсатора.
получаем емкость:
Пример 2: Емкость цилиндрического конденсатора. Заданы: размеры конденсатора (R 1, R 2, l), проницае-мость однородного диэлектрика (ε;). Задавшись зарядом на конденсаторе q, определяем по
где λ= q/l – линейная плотность заряда. Далее определяем напряжение на конденсаторе:
и по определению (5) получаем емкость цилиндрического кон-денсатора
Пример 3: Емкость сферического конденсатора. Заданы: размеры конденсатора (R 1, R 2), проницаемость однородного диэлектрика (ε;).
обкладками Далее рассчитаем напряже-ние на конденсаторе как
и получаем емкость сферического конденсатора
Вопрос 15. Энергия системы неподвижных зарядов. Энергия заряженного проводника и заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии. Энергия взаимодействия системы зарядов
где rik – расстояние между этими зарядами.
Если переписать последнее выражение в виде двух последовательных сумм:
Таким образом, энергия взаимодействия системы зарядов определя-ется как сумма частных произведений (qi∙φi), где φi – потенциал, создаваемый всеми зарядами системы (кроме qi) в точке нахождения заряда qi. n Полная энергия взаимодействия системы непрерывно распределенных зарядов
где φ; – потенциал, создаваемый всеми зарядами системы в элементе объема dV (в том числе самим зарядом dq).
n Энергия уединенного заряженного проводника
n Энергия конденсатора
а с учетом определения емкости можно также записать:
Последние две формулы используются в зависимости от условий работы конденсатора: когда на обкладках поддержи-вается постоянным заряд (конденсатор отключен от источника), то
когда поддерживается постоянным напряжение
n О локализации энергии электрического поля Формула (7) определяет энергию любой электричес-кой системы через заряды и потенциалы, но эту же энергию можно выразить через основную характеристику поля – напряженность Е. Убедимся в этом на простейшем примере – заряженном плоском конденсаторе.
в формулу энергии выражение для емкости плоского конденсатора
получаем:
Вывод: Так как эта плотность энергии определяется через напряженность поля, то можно заключить, что энергия локализована в самом электрическом поле. Вопрос 16. Носители электрического тока в средах. Дрейф заряженных частиц. Сила и плотность тока. Уравнение непрерывности.
Электрический ток, как известно, представляет собой перенос заряда q через ту или иную поверхность S, например, через сечение проводника. Ток может течь в твердых телах (металлы и полупроводники), в жидкостях (электролиты) и в газах (газовый разряд). Для протекания тока необходимо наличие в данной среде свободных заряженных частиц, которые принято называть носителями тока. Носителями тока в проводящей среде могут быть электроны, ионы, либо макрочастицы, несущие на себе избыточный заряд (например, заряженные пылинки и капельки). При отсутствии электрического поля носители совершают хаотические (тепловые) движения со скоростью v и через любую поверхность S проходит в обе стороны в среднем одинаковое число носителей того и другого знака, так что ток через эту поверхность равен нулю. При включении же электрического поля на хаотическое движение носителей накладывается упорядоченное движение со скоростью u (скорость дрейфа), и через поверхность появляется ток. В этом случае скорость носителей будет (v + u), но так как средний вектор тепловой скорости < v > = 0, то получается, что их средняя скорость < v + u > = < u >. Определение: Э лектрический ток – это направленное упорядоченное движение электрических зарядов.
Единицей измерения силы тока в системе СИ является 1[А].
где dI – сила тока через элементарную площадку dS ^, расположенную в данной точке перпендикулярно направлению движения носителей. За направление вектора j принимают направление вектора скорости упорядоченного движения (дрейфа) положительных носителей.
Поле вектора j можно изобразить графически с помощью линий тока (линий вектора j), которые проводятся так же, как и линии вектора Е.
Причем, сила тока - величина алгебраическая (может быть + I, -I), и ее знак зависит от выбора направления нормали п к поверхности S.
где q – заряд, переносимый за конечное время t через рассматриваемую поверхность. Уравнение непрерывности:
определяет заряд, выходящий в единицу времени из объема V, ограниченного рассматриваемой поверхнос-тью.
Выражение (6) – это интегральная форма уравнения непрерывности, является, по существу, аналитическим выражением закона сохранения заряда в изолированной системе.
так как плотность заряда зависит от времени и от координат, а интеграл зависит только от времени.
Это дифференциальная форма записи уравнения непрерывности. Вопрос 17. Электрическое поле в проводнике с током. Силовые линии поля и линии тока. Однородные и неоднородные электрические цепи. Сторонние силы. Эдс цепи.
Поэтому в замкнутой цепи наряду с участками, на которых положительные носители движутся в направлении Е (т. е. в сторону убывания потенциала), должны быть участки, где перенос положительных зарядов происходит в направлении возрастания потенциала, т.е. против кулоновских сил электроста-тического поля. Перемещение зарядов на этих участках возможно лишь с помощью сил неэлектростатической природы, называемых сторонними силами. Сторонние силы могут иметь химическую, фотоэлектрическую, электромагнитную и прочую природу (гальванические элементы, аккумуляторы, динамо-машины). Таким образом, для поддержания тока постоянным необходимы сторонние силы, действующие либо на всей цепи, либо на ее отдельных участках.
Сторонние силы принято характеризовать работой, которую они совершают над перемещающимися по цепи зарядами. Определение: Величина, равная работе сторонних сил над единичным положительным зарядом, называется электродвижущей силой (э. д. с.) действующей в цепи (или на ее участке): E =A/q Размерность э. д. с. в СИ – [B], как у потенциала.
напряженность Е*, как:
где F* - вектор сторонней силы, q – единичный положи-тельный заряд.
на участке цепи 1-2: а разделив на q, получаем э. д. с.,
Таким образом, в электрической цепи, состоящей из системы проводников и источников тока, в общем случае, действует как кулоновское поле с напряженностью Е, так и поле сторонних сил с напряженностью Е*, т.е. – результирующее поле Е = Екул + Е*, которое воздействует на заряд q с силой: F = F кул + F* = q∙;(E кул + E*)
Умножить на эдс12.
Определение: Величина, численно равная работе, совершаемой кулоновскими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения (или просто н апряжением) на данном участке цепи 1-2:
Плюс ЭДС12. Участок цепи, на котором не действуют сторонние силы, называется однородным, для такого участка: U 12 = φ;1 – φ;2. Участок цепи, на котором на носители тока действуют сторонние силы, называется неоднородным, для него: U 12 = (φ;1 – φ;2) + E 12. Вопрос 18. Закон Ома в интегральной и дифферинциальной форме. Удельное сопротивление и электропроводность среды.
n Закон Ома в интегральной форме Немецкий физик Г. Ом в 1826 г. экспериментально установил закон, согласно которому:
Здесь U = φ;1 – φ;2, R – электрическое сопротивление проводника. Выражение (16) принято рассматривать как интегральную форму закона Ома.
Так для однородного цилиндрического проводника имеем: где r - удельное электрическое сопротивление материала проводника в [Ом.м], l – его длина, а S – сечение проводника n Закон Ома в дифференциальной форме Рассмотрим изотропный проводник, в котором упорядоченное движение носителей тока происходит в направлении вектора Е или иначе: вектора j и E сонаправлены. Выделим мысленно в окрестности некоторой точки проводящей среды элементарный цилиндрический объем с образующими, параллельными векторам j и E, основанием dS и длиной dl.
где σ = 1/ r - электропроводность материала проводника (размерность σ; в СИ: 1 [См/м]).
Замечание: Если электроток обусловлен носителями одного знака, то можно записать j = e∙n∙; u и, сравнивая с (17), заключаем: скорость дрейфа и пропорциональна напряжен-ности поля Е, т. е. силе, сообщающей носителям это движение. А из механики известно, что пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызвавшей само движение, на тело также дейст-вует сила сопротивления среды. В нашем случае протекания тока в среде эта сила определяется взаимодействием носителей тока с частицами среды (проводника) и обусловливает электро-сопротивление проводника. В связи с этим дополнительно носители характеризуются подвижностью b, которая определяется как отношение b = u / E. Вопрос 19. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи.
n Закон Ома для неоднородного участка цепи На неоднородном участке электроцепи на носители тока действуют, кроме кулоновских сил F кул = е∙ Е, еще и сторонние силы F* = e∙; E*, которые также вызывают направленное движение зарядов. Очевидно, что средняя скорость и в этом случае пропорциональна суммарной силе е∙;(Е + Е*). Соответственно и плотность тока на таком участке будет пропорциональна сумме (Е + Е*): j = σ∙;(Е + Е*) (18) Выражение (18) является дифференциальной формой закона Ома для неоднородной цепи. Для случая тонких проводников (или контура тока в объемном проводнике) и совпадения направления тока с осью проводника плотность тока j можно считать постоянной во всех точках сечения провода S. Разделив (18) на σ; и умножив скалярно на элемент провода dl, взятый по направлению от сечения 1 к сечению 2, получаем при последующем интегрировании по длине 1-2:
где jl = I / S, причем I = const (по условию); получаем левый интеграл
где - полное сопротивление участка цепи между сечением 1 и сечением 2. Таким образом, интегральное уравнение преобразу-ется к виду: I∙R = (φ;1 – φ;2) + E 12 (19) или [(φ;1 – φ;2) + E 12] (20) Выражения (19) и (20) являются интегральными фор-мами закона Ома для неоднородного участка цепи.
Замечание: Э. д. с. E 12, как и ток I, - алгебраическая величина: если э. д. с. способствует движению положительных носителей в выбранном направлении (1-2), E 12> 0, а если – препятствует, то E 12 < 0. R – это полное сопротивление цепи (с учетом rисточ).
|

 Вблизи пов-ти раздела двух диэлектриков
Вблизи пов-ти раздела двух диэлектриков 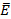 и
и  должны удовлетворять условиям, которые вытекают из соотношений:
должны удовлетворять условиям, которые вытекают из соотношений:
 .
. ,
,
 -
- 


 - угол падения линии электрического смещения,
- угол падения линии электрического смещения,  - угол отражения линии электрического смещения.
- угол отражения линии электрического смещения. Следовательно отношение не зависит от заряда и для каждого уединенного проводника имеет свое конкретное значение. Эту величину принято называть электроемкостью проводника (или просто емкостью проводника) и обозначать:
Следовательно отношение не зависит от заряда и для каждого уединенного проводника имеет свое конкретное значение. Эту величину принято называть электроемкостью проводника (или просто емкостью проводника) и обозначать: Емкость конденсатора определяется как отношение заряда конденсатора к разности потенциалов между его обкладками (иначе: отношение заряда к напряжению на конденсаторе U), т. е.
Емкость конденсатора определяется как отношение заряда конденсатора к разности потенциалов между его обкладками (иначе: отношение заряда к напряжению на конденсаторе U), т. е. Пусть площадь обкладок конденсатора S, а его заряд q, тогда поле между обкладками согласно теореме Гаусса:
Пусть площадь обкладок конденсатора S, а его заряд q, тогда поле между обкладками согласно теореме Гаусса:
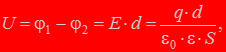 Далее определив напряжение на конденсаторе
Далее определив напряжение на конденсаторе
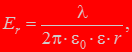 теореме Гаусса поле между обкладками
теореме Гаусса поле между обкладками


 Задавшись зарядом на конденсаторе q, определяем по теореме Гаусса поле в сферическом зазоре между
Задавшись зарядом на конденсаторе q, определяем по теореме Гаусса поле в сферическом зазоре между
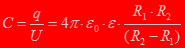

 Ранее было получено выражение для потенциальной энергии взаимодействия двух точечных зарядов qi и qk:
Ранее было получено выражение для потенциальной энергии взаимодействия двух точечных зарядов qi и qk: Теперь рассмотрим систему из N- точечных зарядов: q 1, q 2 ,.., qi,…, qN. Еще в механике было доказано, что энергия взаимодействия системы материальных точек (а сейчас точечных зарядов) равна сумме энергий взаимодействия каждой i- ой точки (i- ого заряда) со всеми оставшимися точками (зарядами), взятых попарно:
Теперь рассмотрим систему из N- точечных зарядов: q 1, q 2 ,.., qi,…, qN. Еще в механике было доказано, что энергия взаимодействия системы материальных точек (а сейчас точечных зарядов) равна сумме энергий взаимодействия каждой i- ой точки (i- ого заряда) со всеми оставшимися точками (зарядами), взятых попарно:
 Если заряды распределены непрерывно (допустим, есть заряженное тело), то, разлагая заряженную систему на совокупность элементарных зарядов dq = ρ∙dV и переходя от суммирования в (6) к интегрированию по объему, получаем:
Если заряды распределены непрерывно (допустим, есть заряженное тело), то, разлагая заряженную систему на совокупность элементарных зарядов dq = ρ∙dV и переходя от суммирования в (6) к интегрированию по объему, получаем: Пусть проводник имеет заряд q и потенциал φ;. Поверхность проводника является эквипотенциальной, т.е. везде, где есть заряд, значение φ – одинаково. Поэтому для проводника в формуле (7) потенциал можно вынести из-под знака интеграла и тогда энергию заряженного проводника можно определить как
Пусть проводник имеет заряд q и потенциал φ;. Поверхность проводника является эквипотенциальной, т.е. везде, где есть заряд, значение φ – одинаково. Поэтому для проводника в формуле (7) потенциал можно вынести из-под знака интеграла и тогда энергию заряженного проводника можно определить как а с учетом определения емкости (3) можно также записать:
а с учетом определения емкости (3) можно также записать: Пусть +q и φ;1 – заряд и потенциал положительно заряженной обкладки, а −q и φ;2 – заряд и потенциал отрицательно заряженной обкладкиконденсатора. Тогда, воспользовавшись формулой (7) и разбив интеграл на две части (для одной и другой обкладок), получим энергию заряженного конденсатора
Пусть +q и φ;1 – заряд и потенциал положительно заряженной обкладки, а −q и φ;2 – заряд и потенциал отрицательно заряженной обкладкиконденсатора. Тогда, воспользовавшись формулой (7) и разбив интеграл на две части (для одной и другой обкладок), получим энергию заряженного конденсатора

 (конденсатор подключен к источнику питания), то
(конденсатор подключен к источнику питания), то
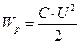 Пренебрегая искажением поля у краев пластин, будем считать поле между обкладками однородным. Подставив
Пренебрегая искажением поля у краев пластин, будем считать поле между обкладками однородным. Подставив
 Так как для плоского конденсатора U/d = E и S∙d = V (объем между обкладками), то его энергию можно также представить:
Так как для плоского конденсатора U/d = E и S∙d = V (объем между обкладками), то его энергию можно также представить: Так как электрическое поле в плоском конденсаторе однородно, то заключенная в нем энергия распределя-ется с постоянной (объемной) плотностью
Так как электрическое поле в плоском конденсаторе однородно, то заключенная в нем энергия распределя-ется с постоянной (объемной) плотностью В общей теории доказывается, что в случае изотроп-ного диэлектрика (когда Е ↑↑ D) полную энергию поля можно определить как:
В общей теории доказывается, что в случае изотроп-ного диэлектрика (когда Е ↑↑ D) полную энергию поля можно определить как: где учтено, что D = ε;0 ∙ε∙; E. При этом объемную плотность энергии электрического поля можно рассчитывать по формулам:
где учтено, что D = ε;0 ∙ε∙; E. При этом объемную плотность энергии электрического поля можно рассчитывать по формулам: Количественной характеристикой электрического тока является сила тока I, т. е. величина заряда, пере-носимого через рассматриваемую поверхность S в единицу времени:
Количественной характеристикой электрического тока является сила тока I, т. е. величина заряда, пере-носимого через рассматриваемую поверхность S в единицу времени: Электрический ток может быть распределен по поверхности неравномерно. Поэтому для более детальной характеристики тока вводят вектор плотности тока j. Модуль этого вектора равен отношению:
Электрический ток может быть распределен по поверхности неравномерно. Поэтому для более детальной характеристики тока вводят вектор плотности тока j. Модуль этого вектора равен отношению:
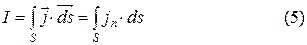 Зная вектор плотности тока j в каждой точке пространства (интересующей нас поверхности S), можно найти силу тока через поверхность:
Зная вектор плотности тока j в каждой точке пространства (интересующей нас поверхности S), можно найти силу тока через поверхность: Ток, не изменяющийся со временем, называется постоянным, для него справедливо равенство:
Ток, не изменяющийся со временем, называется постоянным, для него справедливо равенство: Пусть в некоторой проводящей среде течет ток через замкнутую поверхность S, для которой определим положительную внешнюю нормаль п. Тогда интеграл
Пусть в некоторой проводящей среде течет ток через замкнутую поверхность S, для которой определим положительную внешнюю нормаль п. Тогда интеграл В силу закона сохранения заряда эта величина должна быть равна скорости убывания заряда, содержащегося в объеме V, т. е. имеет место:
В силу закона сохранения заряда эта величина должна быть равна скорости убывания заряда, содержащегося в объеме V, т. е. имеет место:

 согласно теореме Остроградского-Гаусса как
согласно теореме Остроградского-Гаусса как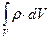 тогда получаем:
тогда получаем: Последнее равенство должно выполняться при произвольном выборе объема dV, а это возможно лишь тогда, когда в каждой точке пространства будет выполняться условие:
Последнее равенство должно выполняться при произвольном выборе объема dV, а это возможно лишь тогда, когда в каждой точке пространства будет выполняться условие:
 Циркуляция вектора Е электростатического поля равна 0, т. е.
Циркуляция вектора Е электростатического поля равна 0, т. е. По аналогии с электростатическим полем Е, проявляющим себя в кулоновском силовом взаимо-действии зарядов, вводят поле сторонних сил и его
По аналогии с электростатическим полем Е, проявляющим себя в кулоновском силовом взаимо-действии зарядов, вводят поле сторонних сил и его По определению работа сторонних сил над зарядом q
По определению работа сторонних сил над зарядом q действующую на этом участке:
действующую на этом участке: А взяв циркуляцию вектора напряженности поля сторонних сил, получаем э. д. с., действующую во всей цепи:=
А взяв циркуляцию вектора напряженности поля сторонних сил, получаем э. д. с., действующую во всей цепи:= Работа, совершаемая этой силой над зарядом на участке цепи 1-2:
Работа, совершаемая этой силой над зарядом на участке цепи 1-2:
 сила тока, протекающего по однородному проводнику (в смысле отсутствия сторонних сил), пропорциональна разности потенциалов на его концах, т. е. напряжению на проводнике:
сила тока, протекающего по однородному проводнику (в смысле отсутствия сторонних сил), пропорциональна разности потенциалов на его концах, т. е. напряжению на проводнике: Единицей измерения сопротивления в СИ является 1[Ом] = 1[B] / 1[A]. Сопротивление R зависит от формы и размеров проводника, свойств материала, температу-ры, распределения тока по объему проводника.
Единицей измерения сопротивления в СИ является 1[Ом] = 1[B] / 1[A]. Сопротивление R зависит от формы и размеров проводника, свойств материала, температу-ры, распределения тока по объему проводника. На основании интегрального закона Ома I= U/R, подставляя выражение для тока, текущего через сечение dS с плотностью j, как I =j∙dS, напряжение на цилиндри-ческом элементе U = E∙dl и его сопротив-ление R = r∙dl/dS, имеем:
На основании интегрального закона Ома I= U/R, подставляя выражение для тока, текущего через сечение dS с плотностью j, как I =j∙dS, напряжение на цилиндри-ческом элементе U = E∙dl и его сопротив-ление R = r∙dl/dS, имеем: отсюда получаем плотность тока
отсюда получаем плотность тока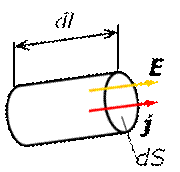
 Таким образом, получаем дифференциальную форму закона Ома в векторном виде:
Таким образом, получаем дифференциальную форму закона Ома в векторном виде: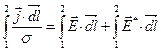

 Далее записав сумму двух интегралов в последнем выражении как (φ;1 – φ;2) + E 12 и заменив σ = 1/ r,
Далее записав сумму двух интегралов в последнем выражении как (φ;1 – φ;2) + E 12 и заменив σ = 1/ r,



