Список вопросов
Суть метода: при перемещении объекта (крови) относительно неподвижного приёмника происходит изменение частоты УЗ-сигнала, отражённого от объекта. Этот метод используется при УЗ-исследовании движущихся структур.
При приближении объекта к приёмнику частота отражённого сигнала «Öотр» возрастает, при удалении – уменьшается. Это явление называется Доплеровский сдвиг частот. Формула для расчётов Доплеровской частоты «Öд»: 2Ö0 × υ ×cosj
с Ö0 – зондирующая частота, посылаемая источником; υ – скорость движущегося объекта; с – скорость УЗ в среде; j– угол между УЗ-лучом и направлением движения объекта.
Этот метод применяется: – Для исследования скорости кровотока; – Для исследования аорты сердца; – В акушерстве и гинекологии для контроля за развитием пола; – В кардиологии. Применение УЗ в медицине: 1. В терапии – оказывает болеутоляющее действие. Противовоспалительное, спазматическое, тепловое, механическое (микромассаж) действие. УЗ рекомендуется применять в комплексе с другими терапевтическими методами. 2. В хирургии – для резки биологических и костных тканей, для сварки костей. 3. В нейрохирургии – для разрушения злокачественной опухоли головного мозга (благодаря способности УЗ к фокусировке). 4. В офтальмологии – оказывает лечебное действие для больных с проникающими ранениями роговицы, с рубцами, кровоизлияниями в стекловидном теле. 5. В отоларинтологии – воздействие УЗ на воспалительные миндалины.
Список вопросов 1. Электрический заряд. Закон Кулона. Напряженность электростатического поля. Силовые линии. Принцип суперпозиции и его применение к расчету поля бесконечно длинной равномерно заряженной нити. 2. Понятие потенциала электростатического поля. Работа поля по перемещению зарядов. Циркуляция вектора Е по замкнутому контору. 3. Понятие градиента. Связь вектора Е и потенциала 4. Теорема Гаусса в интегральной и дифференциальной форме. 5. Теорема Гаусса в дифференциальной форме. Уравнение Пуассона. 6. Применение теоремы Гаусса для расчета полей равномерно заряженной плоскости и цилиндра. 7. Электрическое поле равномерно заряженное на поверхности сферы. Графики для напряженности и потенциала электростатического поля. 8. Расчет вектора напряженности электростатического поля равномерно заряженного по объему шара. 9. Проводник в электростатическом поле. Электростатическая индукция. Поле вблизи поверхности заряженного проводника. Результирующее поле и потенциал заряженного проводника. 10. Электрический диполь: его характеристики и собственное поле. Поведение диполя в однородном и неоднородном электростатических полях. 11. Диэлектрики в электростатическом поле (поляризация). Поле в диэлектрике. Поляризованность. Свободные и связанные заряды. Связь поляризованности и поверхностной плотности связанных зарядов. Связь поляризованности и объёмной плотности связанных зарядов. 12. Т-ма Гаусса для диэлектриков. Обобщённая т-ма Гаусса. Вектор электрического смещения. Сторонние и связанные заряды. Связь векторов E, Р и D. 13. Поле на границе раздела двух однородных диэлектриков. Условия преломлённости векторов E и D. 14. Электроемкость. Емкость плоского, цилиндрического и сферического конденсаторов. 15. Энергия системы неподвижных зарядов. Энергия заряженного проводника и заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии. 16. Носители электрического тока в средах. Дрейф заряженных частиц. Сила и плотность тока. Уравнение непрерывности 17. Электрическое поле в проводнике с током. Силовые линии поля и линии тока. Однородные и неоднородные электрические цепи. Сторонние силы. Эдс цепи 18. Закон Ома в интегральной и дифферинциальной форме. Удельное сопротивление и электропроводность среды 19. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи 20. Закон Джоуля-Ленца в интегральной и дифференциальной форме 21. Обобщенная сила Лоренца. Движение заряженной частицы в однородных электрическом и магнитном полях. Определение удельного заряда частицы. 22. Магнитное поле тока в вакууме. Закон Био-Савара. Принцип суперпозиции для магнитных полей и его применение для расчета поле кругового тока. 23. Закон Ампера. Магнитный момент контура с током. Контур с током в магнитном поле. Силы и момент сил, действующих на контур, в однородном и неоднородном магнитном поле. 24. Работа по перемещению проводника с током в магнитном поле. Понятие магнитного потока. Потокосцепление. 25. Циркуляция и ротор вектора индукции магнитного поля. Теорема Гаусса для магнитного поля. 26. Расчет магнитных полей соленоида и тороида с использованием теоремы о циркуляции вектора H. 27. Намагниченность вещества. Циркуляция вектора намагниченности. Магнитная восприимчивость и магнитная проницаемость. Связь векторов магнитного поля: B, J, H. 28. Магнитное поле в веществе. Диамагнетики, парамагнетики, ферромагнетики и особенности в их намагниченности. 29. Поле на границе раздела двух однородных магнетиков. Условия преломления для векторов B и H. 30. Закон Фарадея для электромагнитной индукции. Правило Ленца. Индуктивность контура. Расчет индуктивности соленоида. 31. Явления самоиндукции и взаимной индукции. Вихревые токи. 32. Энергия тока в контуре, обладающем индуктивностью L. Энергия магнитного поля, объемная плотность этой энергии. 33. Обобщение Максвеллом закона электромагнитной индукции. Понятие вихревого электрического поля. Циркуляция вектора Е 34. Циркуляция вектора И с позиций теории Максвелла. Ток смещения. Закон полного тока. 35. Система уравнений Максвелла в интегральной и дифференциальной формах. 36. Распространение электромагнитных волн В электронейтральной непроводящей среде. Волновое уравнение и его решение. Скорость электромагнитных волн. 37. Плоская электромагнитная волна: ее уравнения и свойства (взаимная ортогональность E, Н и v синфазность, поперечностъ). Связь мгновенных значений векторов Е, Н в электромагнитной волне. 38. Излучение электромагнитных волн ускоренно движущимися зарядами и диполем.Вибратор Герца. 39. Энергия и импульс электромагнитного поля. Вектор Пойнтинга. Теорема Пойнтинга (формулировка). 40. История взглядов на природу света. Волновая и корпускулярная теории света. Шкала электромагнитных излучений. 41. Амплитуда и интенсивность электромагнитной волны. Световой вектор. Показатель преломления среды. Длина электромагнитной волны в разных средах. 42. Электромагнитная волна на границе раздела двух диэлектрических сред. Коэффициенты отражения и пропускания. 43. Принцип суперпозиции электромагнитных волн. Интерференция света. Интерференционное уравнение. Взаимная когерентность световых волн. 44. Интерференция от двух когерентных источников. Условия наблюдения на экране интерференционных максимумов и минимумов. Интерференционная зона, ширина интерференционной полосы. 45. Временная когерентность электромагнитных волн: время и длина когерентности (на примере опыта Юнга). 46. Пространственная когерентность электромагнитных волн (на примере опыта Юнга), ширина когерентности. 47. Интерференция в тонких пленках. Полосы равного наклона и равной толщины. Кольца Ньютона. 48. Дифракция света. Виды дифракции. Принцип Гюйгенса-Френеля. 49. Метод зон Френеля. Расчет амплитуды и интенсивности дифрагированной волны. Векторная диаграмма (спираль Френеля). 50. Дифракция Френеля на круглом отверстии Условия минимумов и максимумов в Дифракци 51. Дифракции Фраунгофера на щели. Условия Минимумов и максимумов в дифракционной картине от щели. Распределение интенсивности. 52. Предельный переход от волновой оптики к геометрической и условия наблюдения видов дифракции. 53. Дифракционная решетка как спектральный прибор. Главные максимумы и интерференционные минимумы. Общая дифракционная картина от решетки 54. Спектральные характеристики дифракционной решетки. Угловая дисперсия (определение и расчет). Область дисперсии. 55. Спектральные характеристики дифракционной решетки. Разрешающая способность (определение и вывод из критерия Рэлея). 56. Поляризация света. Естественный и поляризованный свет. Виды поляризации. Графический способ представления поляризации. 57. Частично поляризованный свет. Степень поляризации. 58. Поляризаторы и анализаторы. З-н Малюса. 59. Поляризация света при отражении и преломлении. З-н Брюстера. 60. Поляризация при двойном лучепреломлении. Обыкновенный и необыкновенный лучи. Распостранение света в одноосных кристаллах. Поляризационная призма и поляроид. Призма Николя. 61. Тепловое излучение и его свойство Основные характеристики теплового излучения. Понятии: абсолютно черное тело (АЧТ), серое тело. 62. Закон Кирхгофа для теплового излучения. Расчет испускательной способности реальных излучателей. 63. Закон Стефана-Больцмана и закон смещения Вина для АЧТ. Спектр теплового излучения), 64. Гипотеза и универсальная формула Планка для спектральной плотности энергетической светимости АЧТ. 65. Корпускулярные свойства света. Внешний фотоэффект и его законы. Формула Эйнштейна. 66. Корпускулярные свойства света. Эффект Комптона Комптоновская длина волны. 67. Корпускулярно-волновой дуализм материи. Волновые свойства микрочастиц. Гипотеза де Бройля. Волны де Бройля Опыты Девиссона - Джермера по дифракции электронов 68. Соотношении неопределенностей Гейзенберга, их применение и следствия. 69. Волновая ф-ция, ее назначение и физический смысл. Пл-ть вер-ти обнаружения частицы. Требования (условия) для волновой ф-ции. Принцип суперпозиции состояний 70. Стационарные состояния и стационарное ур-ие Шредингера. Собственные значения энергии и собственные ф-ции 71. Микрочастица в одномерной потенциальной яме с бесконечно высокими стенками. Уравнение Шредингера, собственные ф-ции состояния, условие нормировки, квантование энергии частицы 72. Прохождение частицы через высокий потенциальный барьер (туннельный эффект). Коэффициент прохождения (прозрачности) барьера 73. Спектр излучения атома водорода. Ф-ла Бальмера. Постулаты Бора. Элементарная боровская теория водородоподобного атома. Квантование радиусов орбит и энергии электрона. 74. Стационарное уравнение Шредингера для атома водорода. Квантование энергии. Энергия связи электрона. Энергия ионизации. 75. Спин электрона. Собственные механический и магнитный моменты электрона Опыт Штерна - Герлаха. 76. Квантовые системы из одинаковых микрочастиц. Принцип неразличимости тождественных частиц. Бозоны и фермионы. Принцип Паули.
Вопрос 1. Электрический заряд. Закон Кулона. Напряженность электростатического поля. Силовые линии. Принцип суперпозиции и его применение к расчету поля бесконечно длинной равномерно заряженной нити.
Электрический заряд – физическая величина: характеризующая свойство тел или частиц вступать в электромагнитные взаимодействия и определяющая силы и энергии при таких взаимодействиях. Элементарный заряд: «е» = 1,6 * 10-19 Кл Электрический заряд - квантуется Если каким – либо внешним образом (например, путем трения) создать в теле избыток заряженных частиц одного знака (и соответственно недостаток частиц с зарядом противоположного знака) – тело окажется заряженным, т. е. приобретет некоторый электрический заряд Q, который можно представить как: Q = ± N.e, где N – число элементарных заряженных частиц Плотность электрического заряда Так как элементарный заряд очень мал, то образующийся в теле макроскопический заряд Q можно считать изменяющимся непрерывно. Поэтому с целью упрощения математических расчетов заменяют истинное распределение элементарных дискретных зарядов фиктивным непрерывным распределением и вводят соответствующую геометрии тела плотность электрического заряда:
линейная плотность заряда, поверхностная плотность заряда, объемная плотность заряда, где dq – элементарный заряд, заключенный соответственно на элементарной длине dl, на элементарной поверхности dS или в элементарном объеме dV. СВОЙСТВА ЭЛ. ЗАРЯДА: Электрический заряд – релятивистски инвариантен Величина заряда, измеряемая в различных инерциальных системах отсчета, оказывается одинаковой. Закон сохранения электрического заряда Суммарный заряд электрически изолированной системы не изменяется
Закон Кулона: сила взаимодействия F между двумя неподвижными зарядами, находящимися в вакууме, пропорциональная зарядам q1 и q2, и обратно пропорциональна квадрату расстояния между ними.
Принцип суперпозиции сил
сила, с которой действует на заряд qa заряд qi в отсутствие остальных (N- 1 ) -зарядов.
Напряженность электростатического поля Всякий неподвижный электрический заряд q изменяет определенным образом свойства окружающего его пространства, как говорят, создает в пространстве электростатическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, пробный заряд qпр. испытывает действие силы Кулона F:
Под пробным зарядом qnp. следует понимать единичный, точечный, неподвижный, положительный заряд.
Измеряется в вектор напряженности можно определить как силу, действующую на пробный заряд, помещенный в данную точку поля. В связи с этим напряженность Е считают силовой характеристикой электрического поля. Напряженность поля точечного заряда
Силовые линии Эти линии проводят так, чтобы касательная к ним в каждой точке совпадала с направлением вектора Е, а густота (плотность) линий, пронизывающих единичную ортогональную площадку в данной точке, была равна модулю этого вектора.
Линии Е - незамкнутые линии, они нигде, кроме зарядов, не начинаются и не заканчиваются.
где ri – расстояние между зарядом qi системы и рассматриваемой точкой поля.
В случае непрерывного распределения заряда по объему тела V разбивают его протяженные заряды на достаточно малые элементы величиной dq = ρ .dV, поля которых вычисляют по формуле (3), и вместо суммирования по формуле (4) проводят интегрирование по всему заряженному объему:
Вопрос 2. Понятие потенциала электростатического поля. Работа поля по перемещению зарядов. Циркуляция вектора Е по замкнутому контору. Определение работы при перемещении заряда
Работа этой центральной силы не зависит от траектории, а определяется только положением начальной т. 1 и – конечной т. 2 перемещения заряда qnp,т.е. А12= Ã12, и вычисляется как:
Работа сил консервативного поля может быть представлена также как убыль потенциальной энергии:
Потенциал поля системы точечных зарядов При рассмотрении электростатического поля, создаваемого системой точечных зарядов { q1,q2,…qi,…qN } можно утверждать, что работа сил этого поля над пробным зарядом равна алгебраической сумме работ сил, обусловленных действием каждого заряда qi системы в отдельности:
Работа сил поля над некоторым зарядом q
Если заряд q из точки с потенциалом φ; удаляется на бесконечность (где φ∞= 0), то эта работа будет:
Потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля на бесконечность. Единицей измерения потенциала φ в системе СИ является 1 [B] – это такой потенциал в точке поля, для перемещения в которую из бесконечности заряда q = 1 Кл нужно совершить работу А = 1 Дж. Работа кулоновских сил по замкнутому контуру.
Теорема о циркуляции вектора напряженности
Циркуляция вектора напряженности электростатического поля равна нулю. Принято называть векторное поле, подчиняющееся условию (21) – потенциальным. Следовательно, электростатическое поле – потенциальное поле.
Вопрос 3. Понятие градиента. Связь вектора Е и потенциала
Раскрыв оператор набла, можно записать для проекций вектора Е:
Аналогично для проекции вектора Е на направление силовой линии:
Определение разности потенциалов по заданному полю Е
A12= q . (φ1-φ2).
Поверхность, во всех точках которой потенциал имеет одно и то же значение, называется эквипотенциальной. Вектор Е в каждой точке поля направлен по нормали к эквипотенциальной поверхности, проходящей через данную точку.
Поток вектора напряженности электрического поля
Дивергенция определяет удельную мощность источников (или стоков) рассматриваемого векторного поля.
Вопрос 4. Теорема Гаусса в интегральной и дифференциальной форме.
Теорема Гаусса в электростатике
Доказательство теоремы Гаусса Рассмотрим поле точечного положительного заряда q. Окружим этот заряд произвольной замкнутой поверхностью S и определим поток вектора Е сквозь ее элемент dS:
Вводя телесный угол dΩ;, лучи которого выходят из заряда и опираются на площадку dSп, перпендикулярную радиусу - вектору r (по которому направлен Е), и в соответствии с геометрическим соотношением dSn=r2. dΩ выражение (29) принимает вид:
Интегрирование последнего выражения сводится к интегрированию по всему телесному углу Ω и приводит к доказательству теоремы:
Интегральная форма теоремы Гаусса При рассмотрении полей, создаваемых заряженными телами с объемной плотностью заряда ρ, можно считать, что каждый элементарный объем dV содержит элементарный заряд dq =ρ . dV, и тогда в правой части выражения (28) для теоремы Гаусса имеем вместо суммы точечных зарядов интеграл по объемному заряду, а теорема Гаусса в целом принимает так называемую интегральную форму:
Дифференциальная форма теоремы Гаусса Согласно теореме Остроградского-Гаусса имеем:
Формула (31) является дифференциальной формой теоремы Гаусса
Вопрос 5. Теорема Гаусса в дифференциальной форме. Уравнение Пуассона.
Согласно теореме Остроградского-Гаусса имеем:
Формула (31) является дифференциальной формой теоремы Гаусса.
Вывод уравнения Пуассона В электростатике существуют задачи, в которых распределение зарядов неизвестно, но заданы потенциалы проводников (заряженных тел), их форма и относительное расположение. Требуется определить потенциал φ;(r)в любой точке электрического поля между проводниками. Определим дифференциальное уравнение, которому должна удовлетворять потенциальная функция φ;(r). Для этого в дифференциальную форму теоремы Гаусса ▼ .Е = ρ/ε0 вместо вектора Е подставим его выражение через потенциал Е = -▼φ;, в результате получим общее дифференциальное уравнение для потенциала – уравнение Пуассона:
где оператор Лапласа в декартовой системе координат: Уравнение Лапласа Если между проводниками нет зарядов (ρ;=0), то уравнение (32) переходит в более простое уравнение Лапласа: ▼2 φ = 0 (33) Теорема единственности Определение потенциала сводится к нахождению такой функции φ(r), которая во всем пространстве между проводниками удовлетворяет либо уравнению Пуассона, либо уравнению Лапласа, а на поверхностях самих проводников принимает известные значения: φ1,φ2 и т.д. Эта задача имеет единственное решение. Вопрос 6. Применение теоремы Гаусса для расчета полей равномерно заряженной плоскости и цилиндра. Поле бесконечной равномерно заряженной плоскости

Пусть поверхностная плотность положительного заряда во всех точках плоскости равна σ. Из симметрии задачи следует, что вектор Е перпендикулярен заряженной плоскости, одинаков по модулю и противоположен по направлению в симметричных относительно плоскости точках. Выбрав в качестве замкнутой поверхности цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величиной ∆S, применим теорему Гаусса. Поток Е через боковую поверхность цилиндра равен 0, а - через каждое основание ФЕ0=Е . ∆S; следовательно суммарный поток ФЕ=2ФЕ0=2Е . ∆S. Заряд, заключенный внутри цилиндра σ . ∆S, таким образом, согласно теореме Гаусса имеем уравнение: 2Е.∆S = σ. ∆S/ε0 или Е = σ/2ε 0 Полученный результат свидетельствует об однородности поля. Поле бесконечного равномерно заряженного цилиндра
Пусть электрическое поле создается бесконечной цилиндрической поверхностью радиуса r0, заряженной равномерно так, что на единицу ее длины приходится заряд λ;. Из соображений симметрии следует, что поле здесь имеет радиальный характер, т.е. Е ┴ ОО’, а модуль – Е (r). Выбрав в качестве гауссовой поверхности коаксиальный цилиндр радиуса r, определим поток вектора Е через его боковую поверхность: ФЕ= Еr . 2πr . h, где Еr – радиальная проекция Е (поток через основания цилиндра равен 0). Таким образом, согласно теореме Гаусса получаем уравнение для случая r ≥ r0: Еr . 2πr . h = λ . h/ε0, откуда следует, что Е ( r ) = Er= λ/2πε 0 r. В случае r < r0 гауссова поверхность не содержит внутри себя зарядов, поэтому в этой области поле отсутствует: Е = 0. Вопрос 7. Электрическое поле равномерно заряженное на поверхности сферы. Графики для напряженности и потенциала электростатического поля.
Вопрос 8. Расчет вектора напряженности электростатического поля равномерно заряженного по объему шара.
Вопрос 9. Проводник в электростатическом поле. Электростатическая индукция. Поле вблизи поверхности заряженного проводника. Результирующее поле и потенциал заряженного проводника. Проводник в электростатическом поле.
Тела, в которых часть микроскопических зарядов способна свободно перемещаться в пределах тела, называются проводниками. Они проводят электрический ток посредством этих зарядов, которые принято называть свободными зарядами.
Условия равновесия зарядов на проводнике Поместим металлический проводник во внешнее электростатическое поле (или сообщим ему некоторый заряд q). На свободные заряды проводника будет действовать электрическое поле, в результате чего все отрицательные заряды (электроны) сместятся против поля, а на месте останутся положительные нескомпенсированные заряды атомов. Такое перемещение зарядов будет продолжаться до тех пор (практически это происходит мгновенно), пока не установится определенное распределение зарядов, при котором электрическое поле во всех точках внутри проводника обратится в нуль. Первое условие равновесия зарядов на проводнике: в статическом случае электрическое поле внутри проводника отсутствует, т. е. Е = 0 (1) Поскольку в проводнике всюду Е = 0, то плотность избыточных зарядов внутри проводника также равна нулю (ρ= 0). Избыточные заряды появляются лишь на поверхности проводника с некоторой плотностью σi (эти заряды называют индуцированными), вообще говоря, различной в разных точках его поверхности. Индуцированный заряд находится в очень тонком поверхностном слое толщиной в один-два межатомных расстояний.
Второе условие равновесия зарядов на проводнике: в статическом случае электрическое поле на поверхности проводника всегда ортогонально поверхности в каждой точке, т. е. Е = Е п (2) Следствия из условий равновесия: Так как в состоянии равновесия внутри проводника избыточных зарядов – нет, то удаление вещества из его некоторого внутреннего объема никак не отразится на равновесном расположении зарядов. Т. е. избыточный заряд распределяется на полом проводнике так же, как и на сплошном – по его наружной поверхности. На внутренней поверхности полости в состоянии равновесия избыточные заряды располагаться не могут. Именно на этом свойстве замкнутой полости основана электростатическая защита объектов (экранирование измерительных приборов) от влияния внешних полей с помощью замкнутых металлических оболочек. Расчет поля у поверхности проводника.
Вопрос 10. Электрический диполь: его характеристики и собственное поле. Поведение диполя в однородном и неоднородном электростатических полях. Электрический диполь – это простейшая электрическая система из двух одинаковых по модулю разноименных точечных зарядов + q и – q, находящихся на некотором малом расстоянии l (плечо диполя). Причем, когда говорят о поле диполя, то предполагают сам диполь – точечным, т.е. считают расстояние от диполя до интересующей точки поля r >> l. Прямую, проходящую через оба заряда, принято называть осью диполя. Поле диполя обладает осевой симметрией, поэтому картина поля в любой плоскости, проходящей через ось диполя, будет одной и той же, причем вектор Е лежит в этой плоскости.
Так как r >> l, то можно считать: (r−−r+)≈ l.cosθ и r+.r−≈ r2, тогда формулу (1) получаем в виде:
где p = q . l – электрический момент диполя.
Отсюда модуль полного вектора Е равен:
и после подстановки последнего выражения в формулу для силы получаем:
Направление вектора силы всегда совпадает с вектором
M = (r+ x F+) + (r− x F−) = (r+ x qE+) – (r− x qE−). При достаточно малом расстоянии между зарядами диполя имеем: Е+ ≈ Е− и М = ((r+ - r−) x qE), а с учетом, что (r+ - r−) = l и ql = p, получаем М = (р х Е) = р.Е.sinα (5) Выводы: 1. Момент сил (5) стремится повернуть диполь так, чтобы его дипольный момент р установился по направлению внешнего поля Е – в этом случае (р↑↑Е) положение диполя является устойчивым. 2. Под действием результирующей силы (4) диполь перемещается в область большего поля Е, где больше концентрация силовых линий.
Диэлектрик (изолятор) – тела, не способное проводить электрический ток, в которых все микроскопические заряды связаны друг с другом в пределах молекул. Идеальных диэлектриков не существует. Диэлектрики состоят либо из нейтральных молекул, либо из заряженных ионов, находящихся в узлах кристаллической решётки. Молекулы могут быть: - полярными, у которых центр тяжести отрицательного заряда сдвинут относительно центра тяжести положительного заряда (такие молекулы обладают собственным дипольным моментом); - неполярными, центры тяжести положительных и отрицательных зарядов совпадают (дипольный момент p=0). Связь дипольного момента В отсутствие внешнего электрического поля дипольные моменты молекул диэлектрика либо равны нулю (неполярные молекулы), либо распределены по направлениям в пр-ве хаотическим образом (полярные молекулы). В обоих случаях суммарный дипольный момент диэлектрика равен 0. Под действием внешнего поля диэлектрик поляризуется, т.е. результирующий дипольный момент диэлектрика становится отличным от нуля. Чтобы охарактеризовать поляризацию в данной точке, нужно выделить заключающий в себе эту точку физически бесконечно малый объём ΔV, найти сумму
где Р – поляризованность диэлектрика [ Связь Связанные заряды (q’, Сторонние (свободные) (q, Электрическое поле в диэлектрике по принципу суперпозиции: Связь между Связь между Электрическое смещение (электрическая индукция): Связь Связь между Поток вектора Т-ма Гаусса для Т-ма Гаусса для диэлектриков:
Связанные заряды (q’, Сторонние (q,
|


 Öд =
Öд = . Поток вектора нарпяженности электростатического поля. Дивергенция Е.
. Поток вектора нарпяженности электростатического поля. Дивергенция Е.


 Результирующая сила F, с которой действуют на некоторый выбранный заряд qa все N- другие заряды qi определяется как:
Результирующая сила F, с которой действуют на некоторый выбранный заряд qa все N- другие заряды qi определяется как:


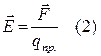 Напряженность электростатического поля численно равно отношению силы, действующей на заряженную частицу со стороны поля
Напряженность электростатического поля численно равно отношению силы, действующей на заряженную частицу со стороны поля или
или  .
. Из формул (1) и (2) следует
Из формул (1) и (2) следует



 Принцип суперпозиции: напряженность Е результирующего поля, создаваемое системой зарядов, равна геометрической сумме напряженности полей, создаваемых в данной точке каждым из зарядов в отдельности.
Принцип суперпозиции: напряженность Е результирующего поля, создаваемое системой зарядов, равна геометрической сумме напряженности полей, создаваемых в данной точке каждым из зарядов в отдельности.
 Рассматривается поле, создаваемое неподвижным точечным зарядом q. В любой точке А этого поля на помещенный пробный заряд qnp действует сила Кулона:
Рассматривается поле, создаваемое неподвижным точечным зарядом q. В любой точке А этого поля на помещенный пробный заряд qnp действует сила Кулона:

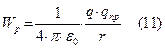
 (10) =>
(10) =>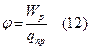 Потенциал численно равен потенциальной энергии, которой обладал бы в данной точке поля единичный положительный точечный заряд. Поэтому потенциал рассматривается как энергетическая характеристика поля.
Потенциал численно равен потенциальной энергии, которой обладал бы в данной точке поля единичный положительный точечный заряд. Поэтому потенциал рассматривается как энергетическая характеристика поля. Потенциал точечного заряда q:
Потенциал точечного заряда q:
 После «нормировки» выражения энергии Wp для некоторой точки на qnp получаемпотенциал электрического поля системы зарядов как алгебраическую сумму потенциалов, созданных каждым из зарядов в отдельности:
После «нормировки» выражения энергии Wp для некоторой точки на qnp получаемпотенциал электрического поля системы зарядов как алгебраическую сумму потенциалов, созданных каждым из зарядов в отдельности: Из определения потенциала (12) следует, что заряд q, находящийся в точке поля с потенциалом φ;, обладает потенциальной энергией Wp= q . φ;. Следовательно, работу сил поля над зарядом q можно представить через разность потенциалов:
Из определения потенциала (12) следует, что заряд q, находящийся в точке поля с потенциалом φ;, обладает потенциальной энергией Wp= q . φ;. Следовательно, работу сил поля над зарядом q можно представить через разность потенциалов: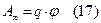
 Зная вектор напряженности электростатического поля Е, работу по перемещению заряда qnp можно определить как линейный интеграл:
Зная вектор напряженности электростатического поля Е, работу по перемещению заряда qnp можно определить как линейный интеграл: Как известно, работа кулоновских сил (как консервативных сил) не зависит от направления перемещения (от пути), т.е. А1а2= Ã1в2. Следовательно можно утверждать, что работа этих сил по замкнутому контуру равна 0. Для этого определяют линейный интеграл по замкнутому контуру L, который в «теории поля» принято называть циркуляцией:
Как известно, работа кулоновских сил (как консервативных сил) не зависит от направления перемещения (от пути), т.е. А1а2= Ã1в2. Следовательно можно утверждать, что работа этих сил по замкнутому контуру равна 0. Для этого определяют линейный интеграл по замкнутому контуру L, который в «теории поля» принято называть циркуляцией: Представление интеграла (19) в виде суммы двух линейных интегралов и с учетом, что А2в1=-Ã1в2, доказывает положение о работе по замкнутому контуру:
Представление интеграла (19) в виде суммы двух линейных интегралов и с учетом, что А2в1=-Ã1в2, доказывает положение о работе по замкнутому контуру: После «нормировки» работы в (19) на величину qnp получаем выражение для записи теоремы о циркуляции вектора Е:
После «нормировки» работы в (19) на величину qnp получаем выражение для записи теоремы о циркуляции вектора Е: . Поток вектора напряженности электростатического поля. Дивергенция Е.
. Поток вектора напряженности электростатического поля. Дивергенция Е. Градиент – это векторная величина, показывающая направление наискорейшего роста некоторой величины.
Градиент – это векторная величина, показывающая направление наискорейшего роста некоторой величины. После подстановки в (22) выражений для силы F = q . Е и энергии Wp= q . φ; и сокращения на постоянную величину q окончательно получаем:
После подстановки в (22) выражений для силы F = q . Е и энергии Wp= q . φ; и сокращения на постоянную величину q окончательно получаем:

 Для этого воспользуемся выражением работы сил поля по перемещению заряда q из т. 1 в т. 2: и приравняем его выражению для той же работы через разность потенциалов:
Для этого воспользуемся выражением работы сил поля по перемещению заряда q из т. 1 в т. 2: и приравняем его выражению для той же работы через разность потенциалов: После сокращения на величину q получаем связь разности потенциалов между рассматриваемыми точками электрического поля и его напряженностью:
После сокращения на величину q получаем связь разности потенциалов между рассматриваемыми точками электрического поля и его напряженностью:
 В «теории поля» принято называть потоком некоторого вектора Е через замкнутую поверхность S интеграл вида:
В «теории поля» принято называть потоком некоторого вектора Е через замкнутую поверхность S интеграл вида:


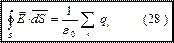 Поток вектора Е через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε0.
Поток вектора Е через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε0.




 Приравнивая правые части последнего выражения и формулы (30), получаем уравнение которое будет выполняться для любого произвольного объема при соблюдении условия:
Приравнивая правые части последнего выражения и формулы (30), получаем уравнение которое будет выполняться для любого произвольного объема при соблюдении условия: ▼;.(-▼ φ;) = ρ/ε0 или ▼ 2 φ = - ρ/ε0, (32)
▼;.(-▼ φ;) = ρ/ε0 или ▼ 2 φ = - ρ/ε0, (32)



 Отсутствие поля внутри проводника означает (в силу Е = - Ñ φ;), что потенциал φ; в проводнике одинаков во всех точках, т. е. любой проводник в электростатическом поле представляет собой эквипотенциальную область, а его поверхность является эквипотенциальной. Из факта эквипотенциальности поверхности проводника следует, что непосредственно у этой поверхности электрическое поле Е направлено по нормали к ней в каждой точке и, соответственно, производная потенциала по касательному направлению
Отсутствие поля внутри проводника означает (в силу Е = - Ñ φ;), что потенциал φ; в проводнике одинаков во всех точках, т. е. любой проводник в электростатическом поле представляет собой эквипотенциальную область, а его поверхность является эквипотенциальной. Из факта эквипотенциальности поверхности проводника следует, что непосредственно у этой поверхности электрическое поле Е направлено по нормали к ней в каждой точке и, соответственно, производная потенциала по касательному направлению
 Пусть интересующий нас участок поверхности проводника граничит с вакуумом. Воспользуемся теоремой Гаусса и определим поток вектора Е через малый цилиндр с основанием ΔЅ, принадлежащим исследуемой поверхности. Так как линии вектора Е перпендикулярны поверхности проводника и внутри проводника Е = 0, то полный поток через цилиндр будет равен только потоку через «наружный» торец этого цилиндра, т. е. Еп∙ΔЅ = σ∙ΔЅ/ε0, где Еп – проекция вектора Е на внешнюю нормаль п, σ – локальная поверхностная плотность заряда на проводнике. После сокращения на ΔЅ получаем:
Пусть интересующий нас участок поверхности проводника граничит с вакуумом. Воспользуемся теоремой Гаусса и определим поток вектора Е через малый цилиндр с основанием ΔЅ, принадлежащим исследуемой поверхности. Так как линии вектора Е перпендикулярны поверхности проводника и внутри проводника Е = 0, то полный поток через цилиндр будет равен только потоку через «наружный» торец этого цилиндра, т. е. Еп∙ΔЅ = σ∙ΔЅ/ε0, где Еп – проекция вектора Е на внешнюю нормаль п, σ – локальная поверхностная плотность заряда на проводнике. После сокращения на ΔЅ получаем: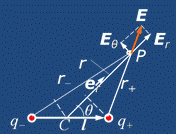
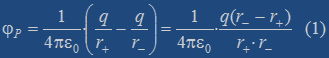 Сначала определим потенциал поля диполя, а затем его напряженность. Согласно формуле для потенци-ала системы точечных зарядов имеем в т. Р:
Сначала определим потенциал поля диполя, а затем его напряженность. Согласно формуле для потенци-ала системы точечных зарядов имеем в т. Р:
 Для нахождения напряженности поля диполя восполь-зуемся соотношением, разложив результирующий вектор Е на два взаимно перпендикулярных направления – вдоль ортов er и eθ, т. е.
Для нахождения напряженности поля диполя восполь-зуемся соотношением, разложив результирующий вектор Е на два взаимно перпендикулярных направления – вдоль ортов er и eθ, т. е. 


 Теперь рассмотрим воздействие неоднородного элект-рического поля на диполь. Пусть Е+ и Е- - напряженности внешнего поля в местах нахождения положительного и отрицательного зарядов диполя. Тогда результирующая сила F = q.E+ - q.E- = q.(E+ - E-). Разность (Е+ - Е-) – это приращение ΔЕ вектора напряженности на отрезке, равном длине диполя, в направлении вектора l. Вследствие малости l можно записать:
Теперь рассмотрим воздействие неоднородного элект-рического поля на диполь. Пусть Е+ и Е- - напряженности внешнего поля в местах нахождения положительного и отрицательного зарядов диполя. Тогда результирующая сила F = q.E+ - q.E- = q.(E+ - E-). Разность (Е+ - Е-) – это приращение ΔЕ вектора напряженности на отрезке, равном длине диполя, в направлении вектора l. Вследствие малости l можно записать: Согласно (4) в однородном поле сила F = 0, так как в этом случае производная по направлению
Согласно (4) в однородном поле сила F = 0, так как в этом случае производная по направлению
 Далее определим момент сил, действующих на диполь. Рассмотрим поведение диполя во внешнем электрическом поле в системе отсчета центра масс (центр диполя С). Согласно определению момент внешних сил F+ = q.E+ и F− = q.E− относительно С равен:
Далее определим момент сил, действующих на диполь. Рассмотрим поведение диполя во внешнем электрическом поле в системе отсчета центра масс (центр диполя С). Согласно определению момент внешних сил F+ = q.E+ и F− = q.E− относительно С равен: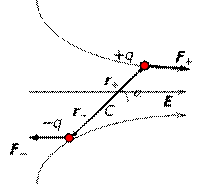
 Диэлектрики в электростатическом поле (поляризация). Поле в диэлектрике. Поляризованность. Свободные и связанные заряды. Связь поляризованности и поверхностной плотности связанных зарядов. Связь поляризованности и объёмной плотности связанных зарядов.
Диэлектрики в электростатическом поле (поляризация). Поле в диэлектрике. Поляризованность. Свободные и связанные заряды. Связь поляризованности и поверхностной плотности связанных зарядов. Связь поляризованности и объёмной плотности связанных зарядов. и напряжённости
и напряжённости  :
: 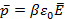 , где
, где  - электрическая постоянная,
- электрическая постоянная,  - поляризуемость молекулы [
- поляризуемость молекулы [  ]. Дипольный момент диполя:
]. Дипольный момент диполя:  .
. моментов, заключённых в этом объёме молекул и взять отношение:
моментов, заключённых в этом объёме молекул и взять отношение:
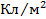 ],
], и
и 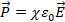 , где χ – не зависящая от Е, диэлектрическая восприимчивость диэлектрика, безразмерна.
, где χ – не зависящая от Е, диэлектрическая восприимчивость диэлектрика, безразмерна.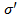 ,
, 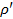 ) – заряды, входящие в состав молекул диэлектрика.
) – заряды, входящие в состав молекул диэлектрика.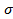 ,
,  )– заряды, не входящие в состав молекул диэлектрика, но находящиеся в пределах диэлектрика, а также заряды, расположенные за пределами диэлектрика.
)– заряды, не входящие в состав молекул диэлектрика, но находящиеся в пределах диэлектрика, а также заряды, расположенные за пределами диэлектрика. , где Е0 – усреднённое поле сторонних зарядов, Е’- усреднённое поле связанных зарядов.
, где Е0 – усреднённое поле сторонних зарядов, Е’- усреднённое поле связанных зарядов. и поверхностной плотностью σ’ связанных зарядов:
и поверхностной плотностью σ’ связанных зарядов:  , где
, где  - проекция поляризованности на внешнюю нормаль к соответствующей пов-ти,
- проекция поляризованности на внешнюю нормаль к соответствующей пов-ти, 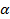 - угол между
- угол между 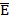 и внешней нормалью к положительно заряженной пов-ти диэлектрика.
и внешней нормалью к положительно заряженной пов-ти диэлектрика.
 [Кл / м2]
[Кл / м2]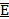 :
:  и
и  :
: 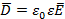 , где
, где  - относительная диэлектрическая проницаемость среды, χ – диэлектрическая восприимчивость диэлектрика.
- относительная диэлектрическая проницаемость среды, χ – диэлектрическая восприимчивость диэлектрика. [Кл]
[Кл] , диф. форма
, диф. форма 





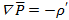

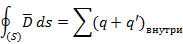

 )– заряды, не входящие в состав молекул диэлектрика, но находящиеся в пределах диэлектрика, а также заряды, расположенные за пределами диэлектрика.
)– заряды, не входящие в состав молекул диэлектрика, но находящиеся в пределах диэлектрика, а также заряды, расположенные за пределами диэлектрика.


