Цифроаналоговые и аналого-цифровые преобразователи
Сигнал любой физической природы (температура, давление, освещенность) с помощью специальных датчиков может быть преобразован в электрическое напряжение или ток. Это позволяет проводить дальнейшую обработку информации, содержащейся в сигнале, с помощью электронных устройств. Выходное напряжение (ток) датчиков обычно пропорционально(ен) уровню преобразуемого сигнала и меняется непрерывно. Такие сигналы относятся к группе аналоговых. Сигналы цифровых систем представляют собой наборы двухуровневых последовательностей. Их совокупность в текущий момент времени может быть интерпретирована как двоичный код числа, соответствующий значению некоторой величины. Таким образом, при необходимости обработкиинформации в цифровых вычислительных машинах данные об уровне сигнала необходимо представить в соответствующей (цифровой) форме. В ряде случаев полученные после цифровой обработки результаты требуется преобразовать в управляющие напряжения. Вследствие существенных отличий и особенностей цифровых и непрерывно меняющихся сигналов для их преобразования из одной формы представления в другую используются специальные устройства – аналого-цифровые и цифроаналоговые преобразователи (АЦП и ЦАП). Первые осуществляют преобразование непрерывно меняющегося напряжения в эквивалентные ему значения цифровых кодов, а вторые трансформируют поступающие на его входы кодовые последовательности в соответствующие уровни выходных напряжений или токов. Аналоговый сигнал, представляемый непрерывной функцией и определенный в любой момент времени, может быть отображен в виде соответствующею графика (рис. 1).
Рис. 1. Графическое представление аналогового сигнала
Любые количественные измерения подразумевают использование эталона, с которым в выбранный момент времени производится сравнение значения измеряемого сигнала рис. 2.
Рис. 2. Использование набора эталонов для измерения уровня сигнала В этом случае его величина может быть представлена числом, равным количеству эталонов, содержащихся в величине сигнала. Для представленной на рис. 2 ситуации Однако при изменении величин сигналов возникают ошибки, связанные с тем, что измеряемый сигнал Таким образом, процесс количественных измерений (преобразования аналоговой формы сигнала в цифровую) связан с появлением погрешности, которая называется шумом квантовании и поабсолютной величине не превышает Вторая проблема, возникающая при количественных измерениях аналоговых сигналов, заключается в том, что процесс измерения требует некоторого времени, поэтому отсчеты значений сигнала могут быть получены лишь через определенные временные интервалы. Процесс представления сигнала в виде совокупности таких отсчетов называется дискретизацией. Очевидно, чем чаще берутся отсчеты, тем меньше будут потери информации о поведении сигнала в промежутках между ними. В то же время из теоремы Котельникова следует, что если ширина спектра сигнала ограничена частотой Процесс аналого-цифрового преобразования предполагает выполнение следующих операций: дискретизация – формирование выборок (отсчетов) мгновенных значений сигнала, квантование – определение количества
эталонных уровней в величине выборки и кодирование – преобразование полученного числа в соответствующие кодовые комбинации. В ходе обратного (цифроаналогового) преобразования формируется сигнал в виде напряжения или тока, пропорциональный числу, представляемому, как правило, двоичным кодом. Уровень выходного сигнала при этом может быть записан в виде Теоретически в ходе преобразования сигнала из цифровой формы представления в аналоговую погрешности отсутствуют. Однако, как и в любых реальных устройствах, на точности преобразования сказывается неидеальностъ узлов, входящих в их состав. Так как при изменении формы представления информация, содержащаяся в исходном сигнале, не меняется, то при последовательном соединении двух идеальных устройств, одно из которых выполняет функцию аналого-цифрового (АЦП), а другое – цифроаналогового преобразователя (ЦАП), сигналы на входе и выходе такой системы (рис. 3) должны быть идентичны. Однако из-за возникновения ошибок при дискретизации и квантовании выходной сигнал
Рис. 3. Трансформация сигнала при прохождении через реальную и идеальную систему АЦП-ЦАП
Рис. 4. Структура сигнала после дискретизации и квантования
Характер этих отличий можно пояснить следующим образом. При аналого-цифровом сигнале преобразовании формирование кода осуществляется в соответствии с соотношением Если данную последовательность кодов подать на цифроаналоговый преобразователь с ценой единицы младшего разряда U0. Равной шагу квантования, то на его выходе сформируется сигнал ступенчатой формы. Он будет совпадать с исходным лишь в точках где уровень входного сигнала равен целому числу шагов квантования. В остальных точках появляются ошибки преобразования, связанные со спецификой трансформации аналогового входного сигнала в цифровую форму.
ЦАП с суммированием весовых токов
Таблица 6 Таблица истинности для ЦАП
1. Подадим на входы ЦАП двоичную комбинацию 0000, на выходе получим 0. Подадим на вход ЦАП двоичную комбинацию 0001. 2. Uвых = КuUвх = 10/150×3 = 0,2 Подадим на вход ЦАП двоичную комбинацию 0010. 3. Uвых = КuUвх = 10/75×3 = 0,4 ………………………………………..
Рис.14 Принципиальная схема ЦАП
Если все переключатели на входе ЦАП будут в положении 1, т. е. двоичная комбинация будет 1111 Uвых = 3 В Кu = 1.
В качестве входного можно использовать любое напряжение питания ±10 В. Можно добавить разрядный переключатель веса 16, в этом случае потребуется резистор R5 с сопротивлением, равным 0,5 R4 (R5 = 9,35 кОм). При этом необходимо изменить сопротивление резистора обратной связи до 5 кОм. На вход ЦАП можно подавать пятиразрядный двоичный код. Данная схема ЦАП имеет низкую точность преобразования.
ЦАП лестничного типа
Таблица истинности остается прежней, только шаг DU = 0,25 В. ЦАП состоит из резисторной схемы и суммирующего усилителя. Схема обеспечивает учет весового множителя на двоичных входах, ее иногда называют схемой R – 2R или схемой лестничного типа. Преимущество состоит в том, что используются резисторы двух номиналов.
Рис.15. Принципиальная схема ЦАП-лесничного типа
Аналого-цифровой преобразователь с динамической компенсацией АЦП – это шифратор специального типа, преобразующий аналоговый сигнал на входе в двоичное слово определенной разрядности на выходе.
Таблица 7 Таблица истинности для АЦП
Как и в любом другом шифраторе необходимо определить ожидаемые значения входных сигналов. Структурная схема АЦП, реализующая связь входных и выходных величин, рис. 16 содержит компаратор, логический элемент И, двоично-десятичный счетчик (ДДС) и ЦАП.
Х
Рис.16 АЦП с динамической компенсацией
К выходу АЦП приложено аналоговое напряжение. Компаратор «проверяет» величину напряжения, поступающего от АЦП. Если Uвх на входе «А» компаратора больше напряжения на входе «В», то с помощью схемы «И» разрешается прохождение тактовых (счетных) импульсов на вход двоично-десятичного счетчика. Счетчик подсчитывает эти импульсы, в результате счета увеличивается двоичное число на выходе. Счет продолжается, если UвхА > UвхВ. Если это условие не выполняется, т. е. напряжение обратной связи с выхода ЦАП превысит аналоговое входное напряжение, в этой точке компаратор останавливает счетчик, который сбросится в нулевое состояние, и счет начнется снова. Предположим, что на выходе компаратора в точке Х действует уровень, меньший единицы. Двоично-десятичный счетчик находится в положении 0000 и к аналоговому входу приложено напряжение 0,55 В. Логическая единица открывает логический элемент «И», и первый импульс от тактового генератора появляется на входе ДДС, который переходит в состояние 0001. Полученная двоичная комбинация появляется на индикаторе и на входе ЦАП. Согласно таблице истинности двоичному числу 0001 соответствует сигнал 0,2 В на выходе. Это напряжение подается на вход «В» и сравнивается с аналоговым сигналом на входе «А» (0,55 и 0,2 В): UА > UВ, поэтому компаратор продолжает вырабатывать сигнал логической «1», который удерживает элемент «И» в открытом состоянии. На вход счетчика поступает следующий счетный импульс, и на выходе получим комбинацию 0010, что соответствует выходному напряжению ЦАП 0,4 В. Счет продолжается пока на выходе не будет 0,6 В, что соответствует двоичной комбинации 0011. Поскольку 0,6 > 0,5 В и компаратор вырабатывает логический «0», запирая элемент «И», ни один счетный импульс не может достичь счетчика. Данный АЦП называется АЦП с динамической компенсацией, что отражает наличие в схеме линейно-нарастающего напряжения.
|



 , а
, а  . После преобразования полученных наборов чисел в двоичные коды информация о величине сигнала окажется представленной в цифровой форме и далее может обрабатываться в цифровых системах.
. После преобразования полученных наборов чисел в двоичные коды информация о величине сигнала окажется представленной в цифровой форме и далее может обрабатываться в цифровых системах. в большинстве случаев меняется непрерывно, а совокупность эталонов
в большинстве случаев меняется непрерывно, а совокупность эталонов  представляет собой дискретный набор значений. Из-за этого в некоторые моменты времени величина измеряемого сигнала не будет соответствовать целому числу эталонов, к примеру,
представляет собой дискретный набор значений. Из-за этого в некоторые моменты времени величина измеряемого сигнала не будет соответствовать целому числу эталонов, к примеру,  . В таких случаях результат измерения округляют до ближайшего целого значения, т.е. принимают, что величина
. В таких случаях результат измерения округляют до ближайшего целого значения, т.е. принимают, что величина 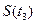 равна либо
равна либо 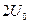 , либо
, либо  . Данная процедура называется квантованием, а величина эталона – шагом квантования. При этом бесконечное множество значений сигнала отображается на конечное множество уровней квантования.
. Данная процедура называется квантованием, а величина эталона – шагом квантования. При этом бесконечное множество значений сигнала отображается на конечное множество уровней квантования. . Погрешность может быть снижена путем уменьшения шага квантования но свести ее к нулю нельзя. Погрешности такого типа относятся к классу методических погрешностей.
. Погрешность может быть снижена путем уменьшения шага квантования но свести ее к нулю нельзя. Погрешности такого типа относятся к классу методических погрешностей. , то при интервалах между отсчетами
, то при интервалах между отсчетами  , по их совокупности можно полностью восстановить исходный сигнал. Таким образом, если отсчеты отстоят друг от друга на интервал, меньший, чем
, по их совокупности можно полностью восстановить исходный сигнал. Таким образом, если отсчеты отстоят друг от друга на интервал, меньший, чем 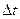 , то погрешностей, связанных с дискретизацией, не будет. Однако сигналы с ограниченным спектром являются математической абстракцией, поэтому в ходе преобразования формы представления сигналов из аналоговой в цифровую возникают ошибки как из-за дискретизации, так и вследствие квантования.
, то погрешностей, связанных с дискретизацией, не будет. Однако сигналы с ограниченным спектром являются математической абстракцией, поэтому в ходе преобразования формы представления сигналов из аналоговой в цифровую возникают ошибки как из-за дискретизации, так и вследствие квантования. , где
, где  – цена единицы младшего разряда, т. е. напряжение, на которое возрастает или уменьшается выходной сигнал при изменении управляющего кода на единицу.
– цена единицы младшего разряда, т. е. напряжение, на которое возрастает или уменьшается выходной сигнал при изменении управляющего кода на единицу.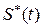 в реальных системах будет отличаться от входного
в реальных системах будет отличаться от входного  .
.

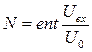 , где ent – функция, означающая целую часть числа, Uвх – входное напряжение, U0 – шаг квантования. В этом случае, если сигнал имеет форму, представленную на рис. 4, в моменты времени, кратные интервалу дискретизации
, где ent – функция, означающая целую часть числа, Uвх – входное напряжение, U0 – шаг квантования. В этом случае, если сигнал имеет форму, представленную на рис. 4, в моменты времени, кратные интервалу дискретизации 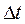 , будут формироваться коды
, будут формироваться коды  соответствующих выборок. Обычно они фиксируются в регистрах памяти и сохраняются, как показано пунктирными линиями, до получения следующего отсчета.
соответствующих выборок. Обычно они фиксируются в регистрах памяти и сохраняются, как показано пунктирными линиями, до получения следующего отсчета.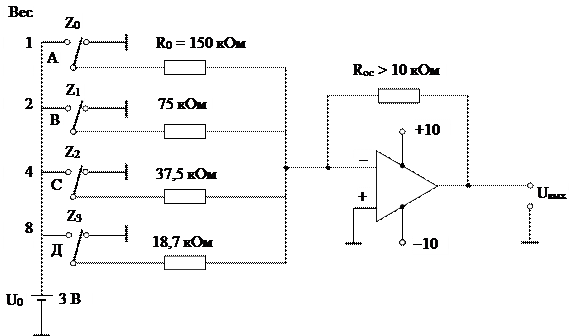
 .
.
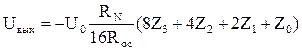 .
.



