Истечение жидкости через отверстия
На рис. 8.1 показано истечение жидкости через отверстие в тонкой стенке.
Рис. 8.1. Истечение жидкости из отверстия в тонкой стенке
Рассмотрим вытекание жидкости из открытого сосуда в атмосферу через отверстие площадью F. При истечении жидкости из отверстия на некотором расстоянии от него происходит сжатие струи. Степень сжатия оценивается коэффициентом сжатия струи ε;, представляющим собой отношение площади сжатого сечения струи Fсж к площади отверстия F [61]
Величина ε; при истечении жидкости из больших резервуаров через малые отверстия равна 0,61 ÷ 0,63. Обозначим постоянную высоту уровня жидкости над центром отверстия через H. Давление и скорость жидкости в сечении 1-1 через Р1; Напишем уравнение Бернулли для сечений 1-1, 2-2, приняв коэффициент скорости α1 = α 2 = 1,
Пренебрегая скоростью движения жидкости в резервуаре (
где
Откуда
в частном случае, когда Р 1 = Р 2 = Ратм
Теоретическая скорость истечения из отверстия равна
Отношение действительной скорости истечения жидкости к теоретической называется коэффициентом скорости
Величина Объемный расход жидкости определяется из выражений
Обозначим произведение Величина μ; называется коэффициентом расхода. Окончательно имеем
Обычно μ и ε определяются опытным путем, а коэффициент φ находится путем вычислений. Например, при ε; = 0,64 и φ; = 0,97; μ; = 0,62. Коэффициент расхода есть отношение действительного расхода к теоретическому расходу. Объемный расход жидкости:
где V – объем жидкости в резервуаре, м3;
Время истечения:
Объемный расход можно также определить по формуле
откуда, при необходимости, определяется d0, Чтобы найти массовый расход, необходимо объемный расход умножить на плотность жидкости (
|


 . (8.1)
. (8.1) 1, в сечении
1, в сечении  . (8.2)
. (8.2) в виду ее малости) и учитывая потери напора только в местном сопротивлении, уравнение Бернулли можно записать в виде:
в виду ее малости) и учитывая потери напора только в местном сопротивлении, уравнение Бернулли можно записать в виде: ,
, – коэффициент местного сопротивления;
– коэффициент местного сопротивления; – удельный вес жидкости, Н/м3.
– удельный вес жидкости, Н/м3. ,
, . (8.3)
. (8.3) . (8.4)
. (8.4) . (8.5)
. (8.5) показывает, какая часть энергии, которой обладает находящаяся в сосуде жидкость, затрачивается на создание скорости и на преодоление сопротивления (например,
показывает, какая часть энергии, которой обладает находящаяся в сосуде жидкость, затрачивается на создание скорости и на преодоление сопротивления (например, 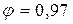 , 97 % расходуется на создание скорости,
, 97 % расходуется на создание скорости,  .
. ,
, ,
,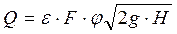 . (8.6)
. (8.6) буквой
буквой 
 . (8.7)
. (8.7) , м3/c, (8.8)
, м3/c, (8.8) – время истечения жидкости, с.
– время истечения жидкости, с. . (8.9)
. (8.9) , (8.10)
, (8.10) или Q.
или Q.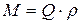 ).
).


