Истечение жидкости при переменном напоре
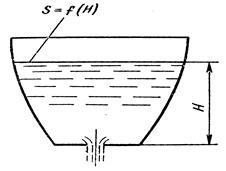
Задача об истечении жидкости при переменном напоре обычно сводится к определению времени опорожнения или наполнения всего сосуда в зависимости от начального наполнения, формы и размеров сосуда и отверстия. Такие задачи решают при наполнении и опорожнении резервуаров, цистерн, водохранилищ, бассейнов, шлюзовых камер. Необходимо иметь в виду, что в этих случаях вследствие непрерывного изменения напора, а следовательно, и непрерывного изменения скоростей и давлений всегда наблюдается неустановившееся движение жидкости, поэтому при расчетах нельзя использовать обычное уравнение Бернулли. При решении таких задач полное время истечения жидкости разделяют на бесконечно малые промежутки, в течение каждого напор считают постоянным, а движение жидкости установившимся. Рассмотрим простейший пример истечения жидкости в атмосферу через донное отверстие площадью s из открытого вертикального цилиндрического сосуда, одинакового по всей высоте поперечного сечения S (рис. 8.4, а).
а) б)
Рис. 8.4. Истечение жидкости при переменном напоре: а – ёмкость с постоянным сечением; б – ёмкость с переменным сечением
Элементарный объем жидкости
где H – глубина жидкости в сосуде в данный момент времени;
Глубину Н в течение времени Вследствие неразрывности потока
откуда
Полное время опорожнения сосуда определяют в результате интегрирования уравнения (8.14)
где Меняя пределы интегрирования в правой части, принимая коэффициент расхода
После интегрирования получим выражение [37]
Формула (8.15) применима также к случаю истечения жидкости из отверстия в боковой стенке сосуда. При этом напор В качестве примера задачи на опорожнение сосудов переменного по
В рассматриваемом случае площадь поперечного сечения сосуда S представляет горизонтальную площадь свободной поверхности жидкости, находящейся в цистерне, соответствующую некоторому уровню z:
где L – постоянная длина цистерны; х – переменная величина, зависящая от значения ординаты z (уровня жидкости в цистерне). Установим эту зависимость. Вертикальное поперечное сечение цистерны представляет собой окружность. Ее уравнение, отнесенное к началу координат, и, следовательно,
Подставив полученное значение S в исходное уравнение, найдем
Рис. 8.5. Общий вид железнодорожной цистерны с нефтепродуктом Вынесем постоянные за знак интеграла и переменим пределы
Сделав подстановку
Для железнодорожной цистерны модели 15-890 длиной L = 10,3 м, радиусом r = 1,2 м эффективным проходным (сливным) сечением отверстия
|


 , прошедшей через отверстие за бесконечно малый промежуток времени
, прошедшей через отверстие за бесконечно малый промежуток времени  , рассчитывают по формуле
, рассчитывают по формуле , (8.13)
, (8.13) – эффективное проходное (сливное) сечение отверстия.
– эффективное проходное (сливное) сечение отверстия. и объем жидкости в нем изменится на
и объем жидкости в нем изменится на 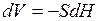 (S – площадь жидкости для цилиндрического вертикального резервуара диаметром d, она равна
(S – площадь жидкости для цилиндрического вертикального резервуара диаметром d, она равна  ). Знак «минус» взят потому, что с течением времени глубина Н уменьшается и, следовательно,
). Знак «минус» взят потому, что с течением времени глубина Н уменьшается и, следовательно, 
 . (8.14)
. (8.14)
 – глубина жидкости в сосуде до начала истечения.
– глубина жидкости в сосуде до начала истечения. и вынося постоянные за знак интеграла, будем иметь
и вынося постоянные за знак интеграла, будем иметь .
. . (8.15)
. (8.15) (высоту столба жидкости) отсчитывают от центра отверстия.
(высоту столба жидкости) отсчитывают от центра отверстия. [37]. Приняв указанное на рисунке расположение координатных осей, получим
[37]. Приняв указанное на рисунке расположение координатных осей, получим (8.16)
(8.16) (8.17)
(8.17) . Отсюда
. Отсюда 
 . (8.18)
. (8.18) ,
,

 . (8.19)
. (8.19) ,
,  , после несложных преобразований в результате интегрирования получим окончательное выражение для определения времени опорожнения цистерны в секундах
, после несложных преобразований в результате интегрирования получим окончательное выражение для определения времени опорожнения цистерны в секундах
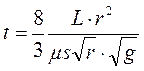 ,
,  . (8.20)
. (8.20)


