Основные теоретические сведения. На практике необходимы устройства, позволяющие при малых габаритах накапливать (конденсировать) большие заряды
На практике необходимы устройства, позволяющие при малых габаритах накапливать (конденсировать) большие заряды. Этим требованиям удовлетворяют конденсаторы: системы из двух проводников. Образующие конденсатор проводники называют обкладками. Внешние поля не должны оказывать влияния на способность конденсировать заряды. Для этого обкладкам придают такую форму и располагают друг относительно друга так, чтобы поле, создаваемое зарядами на обкладках, было сосредоточено между обкладками конденсатора. Этому условию удовлетворяют: две параллельные пластины из проводящего материла, расположенные на малом расстоянии друг от друга, два коаксиальных цилиндра, две концентрических сферы. Соответственно конденсаторы называют: плоскими, цилиндрическими и сферическими (рис. 2.1). Конденсаторы находят широкое применение в электротехнических и радиотехнических устройствах. Способность накапливать заряды называется электрической ёмкостью, которая определяется по формуле
где
Получим формулу ёмкости плоского конденсатора (рис. 2.1а), площадь обкладки которого S, зазор между пластинами d мал по сравнению с линейным размером обкладки
Электроёмкость конденсатора при заданных геометрических размерах может меняться в широких пределах в зависимости от диэлектрической проницаемости диэлектрика. Диэлектрическая проницаемость современных керамических материалов достигает порядка Получим формулу сферического конденсатора, радиус внутренней сферической обкладки которого равен a, внешней – b. Поле, возникающее между обкладками, описывается формулой напряжённости поля точечного заряда
отсюда ёмкость конденсатора
Если Ёмкость цилиндрического конденсатора на единицу длины
Энергия, запасённая в конденсаторе, определяется по формуле
На практике применяется параллельное, последовательное и комбинированное соединение конденсаторов. При параллельном соединении конденсаторов (рис. 2.2) разность потенциалов на каждом конденсаторе одинакова и равна Заряд, накопленный на всех конденсаторах
При последовательном соединении конденсаторов (рис. 2.3) заряды на каждом конденсаторе одинаковы, а суммарное падение напряжения
Полная ёмкость такого соединения определяется из соотношения:
Рассмотрим процесс разряда конденсатора в цепи, электрическая схема которой представлена на рис. 2.4. При замкнутом ключе конденсатор заряжен до разности потенциалов батареи, заряд на конденсаторе В любой момент времени при разряде конденсатора разность потенциалов между его обкладками равна Из равенства падений напряжений на конденсаторе и сопротивлении следует:
Разделяя переменные в уравнении (2.10), получим
Интегрируя и потенцируя выражение (2.11), с учётом начальных условий, находим
Величина Согласно формуле (2.1) для вычисления величины ёмкости при заданном напряжении необходимо определить заряд конденсатора. Это можно сделать двумя способами: методом баллистического гальванометра или регистрируя изменение тока разряда конденсатора со временем. Первый метод применим, когда время
где B – магнитная индукция поля постоянного магнита, S – площадь рамки, N – количество витков в рамке, q – определяемый электрический заряд, прошедший через рамку гальванометра. Если
Тогда начальная кинетическая энергия подвижной системы гальванометра с учётом соотношения (2.14) равна
Движение рамки сопровождается переходом кинетической энергии подвижной системы в потенциальную энергию упругой деформации пружины, равную
При максимальном угле поворота подвижной системы
где Из формулы (2.17) следует, что заряд, прошедший через баллистический гальванометр, пропорционален максимальному углу поворота его подвижной системы из положения равновесия. В этом случае отброс стрелки гальванометра будет пропорционален заряду на конденсаторе, а при постоянном напряжении также и ёмкости конденсатора согласно формуле (2.1). Следовательно, ёмкость конденсатора пропорциональна числу делений, на которое совершает отброс стрелка гальванометра:
где Имея эталонный конденсатор известной ёмкости C, можно определить цену деления гальванометра при измерении ёмкостей по формуле
Зная цену деления При
В этом случае заряд конденсатора будет равен площади под кривой зависимости разрядного тока от времени.
|

 , (2.1)
, (2.1) – величина заряда на каждой обкладке конденсатора;
– величина заряда на каждой обкладке конденсатора;  – разность потенциалов между обкладками. Т.е. ёмкость численно равна заряду, который необходимо сообщить обкладкам для того, чтобы разность потенциалов возросла на единицу. Единицей электроёмкости является фарад (Ф). Фарад – это электроёмкость такого конденсатора, передача которому заряда в один кулон изменяет его разность потенциалов на один вольт
– разность потенциалов между обкладками. Т.е. ёмкость численно равна заряду, который необходимо сообщить обкладкам для того, чтобы разность потенциалов возросла на единицу. Единицей электроёмкости является фарад (Ф). Фарад – это электроёмкость такого конденсатора, передача которому заряда в один кулон изменяет его разность потенциалов на один вольт  .
.
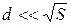 . Поле внутри такого конденсатора можно считать однородным и можно пренебречь краевыми эффектами. Напряжённость поля внутри конденсатора
. Поле внутри такого конденсатора можно считать однородным и можно пренебречь краевыми эффектами. Напряжённость поля внутри конденсатора  , где
, где  – поверхностная плотность распределения заряда на обкладке. Разность потенциалов между обкладками найдём, выбрав линию интегрирования вдоль силовой линии поля
– поверхностная плотность распределения заряда на обкладке. Разность потенциалов между обкладками найдём, выбрав линию интегрирования вдоль силовой линии поля  . Отсюда ёмкость плоского конденсатора
. Отсюда ёмкость плоского конденсатора 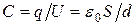 . Если пространство между обкладками заполнено диэлектриком, то напряжённость поля уменьшится в
. Если пространство между обкладками заполнено диэлектриком, то напряжённость поля уменьшится в  раз (
раз ( . (2.2)
. (2.2)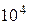 .
. (при значениях
(при значениях  удовлетворяющих условию
удовлетворяющих условию  ). Выбрав линию интегрирования вдоль радиуса, найдём
). Выбрав линию интегрирования вдоль радиуса, найдём , (2.3)
, (2.3) . (2.4)
. (2.4) , то
, то  и
и 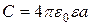 , что есть ёмкость уединённой сферы. Если величина зазора мала по сравнению с радиусами обкладок, то
, что есть ёмкость уединённой сферы. Если величина зазора мала по сравнению с радиусами обкладок, то  и
и  . Тогда
. Тогда  , где
, где  – площадь сферической обкладки. Полученная формула совпадает с формулой ёмкости плоского конденсатора.
– площадь сферической обкладки. Полученная формула совпадает с формулой ёмкости плоского конденсатора.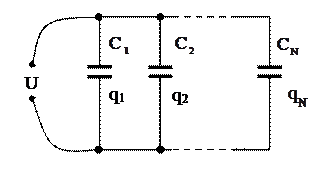

 . (2.5)
. (2.5) . (2.6)
. (2.6) . Согласно формуле (2.1) ёмкость такой системы
. Согласно формуле (2.1) ёмкость такой системы . (2.7)
. (2.7)
 . (2.8)
. (2.8) . (2.9)
. (2.9)

 . После размыкания ключа заряды стекают через сопротивление
. После размыкания ключа заряды стекают через сопротивление  . Через сопротивление течёт уменьшающийся по мере разряда конденсатора ток
. Через сопротивление течёт уменьшающийся по мере разряда конденсатора ток  .
. .
. . (2.10)
. (2.10) . (2.11)
. (2.11) . (2.12)
. (2.12)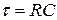 называется постоянной времени для данной цепи. Ёе значение определяет время уменьшения заряда в e раз (e
называется постоянной времени для данной цепи. Ёе значение определяет время уменьшения заряда в e раз (e  2,71).
2,71). разряда конденсатора в данной цепи намного меньше периода
разряда конденсатора в данной цепи намного меньше периода 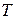 собственных колебаний рамки магнитоэлектрического измерительного прибора
собственных колебаний рамки магнитоэлектрического измерительного прибора  . Такой прибор называется баллистическим гальванометром. При протекании кратковременного тока I по рамке, помещённой между полюсами постоянного магнита, рамка получает импульс момента M амперовых сил
. Такой прибор называется баллистическим гальванометром. При протекании кратковременного тока I по рамке, помещённой между полюсами постоянного магнита, рамка получает импульс момента M амперовых сил , (2.13)
, (2.13) , то можно считать, что за время
, то можно считать, что за время  и начальную угловую скорость
и начальную угловую скорость  . С учётом выражения (2.13) получим
. С учётом выражения (2.13) получим . (2.14)
. (2.14)
 . (2.15)
. (2.15) . С учётом соотношения
. С учётом соотношения 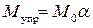 , где
, где 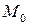 – постоянный коэффициент, а угол
– постоянный коэффициент, а угол  – угол поворота рамки, получим
– угол поворота рамки, получим . (2.16)
. (2.16) вся её кинетическая энергия переходит в потенциальную энергию сжатой пружины. Приравнивая выражения (2.15) и (2.16), находим
вся её кинетическая энергия переходит в потенциальную энергию сжатой пружины. Приравнивая выражения (2.15) и (2.16), находим , (2.17)
, (2.17) – величина, постоянная для данного прибора.
– величина, постоянная для данного прибора. , (2.18)
, (2.18) – число делений,
– число делений,  – коэффициент пропорциональности.
– коэффициент пропорциональности. . (2.19)
. (2.19) .
. применяется второй метод определения заряда конденсатора. Заряд конденсатора при этом определяется по формуле:
применяется второй метод определения заряда конденсатора. Заряд конденсатора при этом определяется по формуле: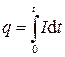 . (2.20)
. (2.20)


