Законы переменного тока.
Рассмотрим подключение цепей к источнику переменной ЭДС. Важность цепей переменного тока объясняется тем, что большое число генераторов переменного тока, вырабатывающих синусоидальное напряжение, производят основную часть всей электроэнергии в мире. Резистор в цепи переменного тока Источник переменной ЭДС вырабатывает синусоидальную ЭДС с частотой
где Если к источнику переменной ЭДС подключен только резистор R (рис. 3.5 а), то согласно закону Ома, сила тока через резистор будет изменяться в соответствии с изменением ЭДС:
где U − напряжение на резисторе в данный момент и
Сила тока и напряжение изменяются в фазе: в те моменты времени, когда напряжение достигает наибольшего значения, сила тока тоже максимальна (рис. 3.5 б). В «положительные» полупериоды ток идёт в одном направлении, в «отрицательные» − в противоположном, так что среднее значение силы тока равно нулю. Однако это не означает, что мощность равна нулю и что резистор не выделяет тепло. Электроны в резисторе движутся то в одну сторону, то в другую, в результате чего выделяется тепло. Мгновенная мощность, рассеиваемая на резисторе R, равна
Поскольку в выражение входит квадрат силы тока, мощность всегда положительна. Средняя мощность равна
Для определения средней мощности важно не просто среднее значение напряжения или силы тока (равное здесь нулю), а среднее значение квадрата напряжения и силы тока: Индуктивность в цепи переменного тока На схеме (рис. 3.6 а) катушка индуктивности L подключена к источнику переменной ЭДС; ёмкостью катушки и её сопротивлением мы пренебрегаем. Следовательно
или
Чтобы найти силу тока, выразим из последнего равенства d I и проинтегрируем:
Полученное выражение можно переписать в виде
где амплитудное значение силы тока
Таким образом, по фазе сила тока отстаёт по фазе от напряжения на 90˚ (рис. 3.6. б). Поскольку сила тока и напряжение сдвинуты относительно друг друга на 90˚, средняя мощность, рассеиваемая катушкой, равна нулю. Энергия источника поступает в катушку, где запасается её магнитным полем, а когда поле убывает, энергия возвращается источнику. Таким образом, в среднем только резистор потребляет энергию источника тока и рассеивает её. Можно написать соотношение между пиковыми значениями силы тока и напряжения на катушке
величина
Переменный ток в RL-цепочке Всякая реальная цепь обладает собственным активным сопротивлением, поэтому реальную цепь, содержащую катушку можно представить как цепь с последовательным соединением резистора R и катушки индуктивности L (рис. 3.7). Найдём полное сопротивление такой цепи, используя полученные выше результаты. Пусть UR и UL − падения напряжения на соответствующих элементах цепи в один и тот же момент времени; U0R и U0L − пиковые значения напряжений на резисторе, катушке и конденсаторе. Фазовые соотношения между силой тока и напряжением на каждом из элементов будут такими же, как для каждого элемента в отдельности: UR совпадает по фазе с током, UL опережает ток на 90˚. И в любой момент времени ЭДС источника e (или U) равна сумме напряжений на отдельных элементах:
Будем считать, что мгновенное значение силы тока одинаково во всех точках цепи. Это допущение оправданно, если частота не слишком велика и соответствующая длина волны намного больше геометрических размеров цепи. Воспользуемся для решения этой задачи методом векторных диаграмм. Каждое напряжение представим в виде вектора в прямоугольной системе координат (х, y); длина вектора характеризует величину пикового напряжения на соответствующем элементе цепи, согласно (3.12) и (3.19) Для удобства начальную фазу тока примем равной нулю:
Итак, при t = 0 сила тока I = 0, и вектор, представляющий I 0, расположен вдоль оси х и направлен в сторону положительных значений х, проекция вектора на ось y равна нулю. Напряжение на резисторе всегда совпадает по фазе с током, и вектор
Представим теперь, что вся диаграмма вращается с угловой скоростью ω. Тогда спустя время t вектор повернётся на угол ωt (рис. 3.8 б). Проекция каждого вектора на ось y будет характеризовать падение напряжения на каждом элементе цепи в момент времени t. Сумма проекций двух векторов на ось y равна проекции их суммы, но сумма проекций в любой момент равна мгновенному падению напряжения на всей цепи, которое совпадает с ЭДС источника e. Поэтому векторная сумма двух векторов равна пиковому значению ЭДС источника e 0. Из рисунка видно, что вектор e 0 составляет угол j с I 0. Вектор e 0 вращается вместе с другими векторами, и мгновенное значение ЭДС равно
Мы видим, что напряжение источника сдвинуто по фазе относительно силы тока на угол
где полное сопротивление цепи
Из рис. 3.8 б можно найти и сдвиг фаз
Определим выделяющуюся в цепи мощность. Мы видели, что мощность рассеивается только на активном сопротивлении R; на реактивном сопротивлении катушки или конденсатора мощность не рассеивается. Следовательно, средняя мощность
Множитель
|

 :
: , (3.11)
, (3.11) − амплитудное (пиковое) значение ЭДС.
− амплитудное (пиковое) значение ЭДС. , (3.12)
, (3.12)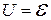 согласно правилу Кирхгофа. Амплитудное значение силы тока равно
согласно правилу Кирхгофа. Амплитудное значение силы тока равно  .
.
 . (3.13)
. (3.13) . (3.14)
. (3.14) и
и 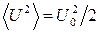 . Извлекая из этих выражений квадратный корень, мы получим среднеквадратичное значение силы тока
. Извлекая из этих выражений квадратный корень, мы получим среднеквадратичное значение силы тока  и напряжения
и напряжения 
 . Среднеквадратичные значения напряжения и силы тока называют эффективными (или действующими значениями). Их можно непосредственно подставлять в формулы для вычисления средней мощности. Другими словами, мощность переменного тока равна мощности постоянного тока с эффективными значениями напряжения и силы тока.
. Среднеквадратичные значения напряжения и силы тока называют эффективными (или действующими значениями). Их можно непосредственно подставлять в формулы для вычисления средней мощности. Другими словами, мощность переменного тока равна мощности постоянного тока с эффективными значениями напряжения и силы тока. , (3.15)
, (3.15) . (3.16)
. (3.16) . (3.17)
. (3.17) ,
, . (3.18)
. (3.18)
 , (3.19)
, (3.19) − реактивное индуктивное сопротивление, также измеряется в омах.
− реактивное индуктивное сопротивление, также измеряется в омах.
 . (3.20)
. (3.20) , а угол между вектором и осью х равен сдвигу фазы напряжения относительно тока (рис. 3.8).
, а угол между вектором и осью х равен сдвигу фазы напряжения относительно тока (рис. 3.8). . (3.21)
. (3.21) также будет направлен вдоль оси х в положительном направлении (при t = 0). Поскольку напряжение на катушке опережает ток по фазе на 90˚, вектор
также будет направлен вдоль оси х в положительном направлении (при t = 0). Поскольку напряжение на катушке опережает ток по фазе на 90˚, вектор  при t = 0 расположен в положительном направлении оси y (рис. 3.8 а).
при t = 0 расположен в положительном направлении оси y (рис. 3.8 а).
 . (3.22)
. (3.22) . Из рис. 3.8 б следует, что
. Из рис. 3.8 б следует, что , (3.23)
, (3.23) . (3.24)
. (3.24)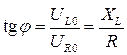 , или
, или  . (3.25)
. (3.25) . Но
. Но  , откуда
, откуда . (3.26)
. (3.26) называется коэффициентом мощности цепи. Для чисто активного сопротивления
называется коэффициентом мощности цепи. Для чисто активного сопротивления 


