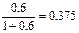Решение
1-2 Задача № 1. Через 5лет сын будет поступать в университет. Сумма требуемого авансового платежа в момент поступления составит 7500долл.Вы планируете также через 3 года сменить свой автомобиль, потратив на это 15 тыс. долл. Каким должен быть взнос в банк, чтобы накопить требуемые суммы, если банк предлагает ставку в размере 12%? Решение n=5лет PV=7500долл r=12% PV1=FV/(1+r)^n=15000/1.12^3=10676.7долл PV2=7500/1.12^5=4255.7долл PV1+PV2=14932.2 долл –требуемая сумма взноса
Задача № 2. Проект, рассчитанный на 15лет, требует инвестиций в размере 150 000 долл. В первые 5лет никаких поступлений не ожидается, однако в последующие 10 лет ежегодный доход составит 50 000 долл. Следует ли принять проект к рассмотрению, если r=15%? Решение n=5 r=15%
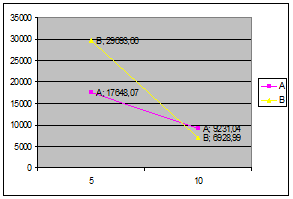
3 Задача № 3. Рассматриваются два альтернативных проекта (руб.): А: -50 000 15625 15625 15625 15625 15625 В: -80 000 - - - - 140 000 Требуется а)найти точку Фишера; б) сделать выбор при r=5% и при r=10% Решение а) В-А: -30000 -15625 -15625 -15625 -15625 124375 При r=5 NPV=-30000-15625/1.05^1-15625/1.05^2….+124375/1.05^5=12045.59 При r=10 NPV==-30000-15625/1.1^1-15625/1.1^2….+124375/1.1^5=-2302,06 IRR=5+12045.59/(12045.59+2302.06)*(10-5)=9.198 При r=9.198 NPV(А)=NPV(B)=-80000+140000/(1+0.09198)^5=10461.72 (9,198;10461,72)- точка Фишера б) При r=5%
При ставке r=5% выбираем проект с большим NPV, т.е. проект В, при ставке r=10% выбираем проект А.
4 Задача № 4. Предприятие рассматривает целесообразность приобретения новой технологической линии. На рынке имеются две модели со следующими параметрами (тыс. долл.): М1 М2 Цена 9500 13000 Генерируемый годовой доход 2100 2250 Срок эксплуатации 8лет 12 лет Ликвидационная стоимость 500 800 Требуемая норма прибыли 11% 11 % Обоснуйте целесообразность приобретения той или иной технологической линии. Решение: Для М1 IC = 9500 n = 8 r1 = 11 % Коэф. эф-ти инвестиций ARR = PN/ (½ (IC+RV)) ARR = 2100/ (½ (9500+500)) = 0,42 = 42 % Год Доход 1 2100 2 2100 3 2100 4 2100 5 2100 6 2100 7 2100 8 2100 Срок окупаемости инвестиций PP = 5 лет NPV = ∑ Pi / (1+r) n – IC NPV1 = 2100/1,111 + 2100/1,112 + 2100/1,113 + 2100/1,114 + 2100/1,115 + 2100/1,116 + 2100/1,117 + 2100/1,118– 9500 =1523,81 тыс.$ PI = ∑ Pi / (1+r) n / IC = 11023,82 / 9500 = 1,16 >1 – проект приемлем r2 = 20 % NPV2 = 2100/1,21 + 2100/1,22 + 2100/1,23 + 2100/1,24 + 2100/1,25 + 2100/1,26 + 2100/1,27 + 2100/1,28 -9500 = -1325,68 IRR = r1* NPV (r1) / (NPV (r1) – NPV (r2)) * (r2 – r1) IRR = 11 * 1523,81/ (1523,81 – (–1325,68)) * (20-11) = 15,81 % > r1 Проект вполне приемлем к реализации, т. к. чистый приведенный доход NPV> 0, индекс рентабельности PI>1, что говорит о том, что с каждого рубля затрат получается 1,16 прибыли, внутренняя норма прибыльности IRR превышает цену капитала. Для М2: IC = 13000 n = 12 r1 = 11 % Коэф. эф-ти инвестиций ARR = PN/ (½ (IC+RV)) ARR = 2250/ (½ (13000+800)) = 0,326 = 32,6 % Год Доход 1 2250 2 2250 3 2250 4 2250 5 2250 6 2250 7 2250 8 2250 9 2250 10 2250 11 2250 12 3050 Срок окупаемости инвестиций PP = 6 лет NPV = ∑ Pi / (1+r) n – IC NPV1 = 2250/1,111 + 2250/1,112 + 2250/1,113 + 2250/1,114 + 2250/1,115 + 2250/1,116 + 2250/1,117 + 2250/1,118 + 2250/1,119 + 2250/1,1110 + 2250/1,1111 + 3050/1,1112 – 13000 =1836,47 тыс.$ > 0 – проект приемлем PI = ∑ Pi / (1+r) n / IC = 14836,47 / 13000 = 1,14 >1 – проект приемлем r2 = 20 % NPV2 = 2250/1,21 + 2250/1,22 + 2250/1,23 + 2250/1,24 + 2250/1,25 + 2250/1,26 + 2250/1,27 + 2250/1,28 + 2250/1,29 + 2250/1,210 + 2250/1,211 + 3050/1,212 – 13000 = 10077,96 – 13000 = –2922,04 IRR = r1* NPV (r1) / (NPV (r1) – NPV (r2)) * (r2 – r1) IRR = 11 * 1836,47/ (1836,47 – (–2922,04)) * (20-11) = 14,5 % > r1 Проект вполне приемлем к реализации, т. к. чистый приведенный доход NPV> 0, индекс рентабельности PI>1, что говорит о том, что с каждого рубля затрат получается 1,14 прибыли, внутренняя норма прибыльности IRR превышает цену капитала.
5-6 Задача № 5. Предприниматель после выхода на пенсию хочет обеспечить себе стабильный доход в течение 20 лет, для этого его ежегодный доход должен составлять 2000 дол. До пенсии осталось 25 лет. Какую сумму должен каждый год вносить предприниматель в банк чтобы его план осуществился, при r = 7%. Решение: 1. А = 2000 дол. r = 7% n = 20 лет
2. FV = 21188 дол. r = 7% n = 25 лет
Предприниматель должен каждый год, в течении 25 лет, вносить в банк по 335 долларов, чтобы его план осуществился.
Задача № 6. Вы имеете возможность профинансировать проект продолжительностью 3 года. Величина требуемых инвестиций 10000 долл., доход по годам ожидается в размере соответственно 5000, 4000, 3000 долл. Стоит ли принимать это предложение, если приемлемая ставка дисконтирования равна 10%? Решение: ARR=
DPP=2 года + 2148,76/3000=2,72 года NPV= PI= R1=10%, R2=12% NPV (r2)= IRR= Вывод: данный проект стоит принять т.к. чистый приведенный эффект больше 0, рентабельность больше 1, т.е. на каждый рубль затрат получаем больше прибыли. Внутренняя норма прибыльности больше цены капитала. 7-8 Задача № 7. Через 4 года ваш сын будет поступать в университет на коммерческой основе. Плата за весь срок обучения составит 5600 долл., если внести ее в момент поступления в университет. Вы располагаете в данный момент суммой в 4000 долл. Под какую минимальную процентную ставку нужно положить деньги в банк, чтобы накопить требуемую сумму? Решение: n = 4 FV = 5600 PV = 4000 r =? FV = PV (1+r) n 5600=4000(1+r) 4 (1+r) 4=5600/4000 (1+r) 4=1,4 1 + r =1,0877 r =0,0877 Чтобы накопить требуемую сумму, необходимо положить деньги в банк под 8,77%. Задача № 8. Проанализировать проекты, если значение коэффициента дисконтирования равно 20% А: -370 - - - - 1000 В: -240 60 60 60 60 - С: -263,5 100 100 100 100 100 1) Чистый приведенный доход: NPV = А: NPV= 1000/1,2 В: NPV= 60/1,2 + 60/1,2 С: NPV= А* 2) Индекс рентабельности инвестиций: PI = А: PI= 401,88/370 = 1,086>1 т.е. проект выгоден В: PI= 155,32/240 = 0,647<1, т.е. проект не выгоден С: PI= 299,06/263,5 = 1,135>1, т.е. проект выгоден 3) Модифицированная внутренняя норма прибыли: MIRR А: PV= TV= TV>PV 370=1000/(1+MIRR) MIRR= 0,22 = 22% > 20% - проект выгоден В: PV= TV= TV>PV 240=386,496/(1+MIRR) MIRR= 0,0999 = 9,99 % < 20% - проект не выгоден C: PV= TV= TV>PV 263,5 =744,16/(1+MIRR) MIRR= 0,2308 = 23,08 % > 20% - проект выгоден Вывод: Проект В не целесообразен, т.к. NPV<0, PI<1, MIRR<20%. А проекты А и С выгодны, т.к. имеют приемлемые значения аналитических коэффициентов. Проект С прибыльнее проекта А. 9-11 Задача № 9. Вам необходимо накопить 25 тыс. долл. за 8 лет. Каким должен быть ежегодный взнос в банк (схема пренумерандо), если банк предлагает 10% годовых. Какую сумму нужно было бы единовременно положить в банк сегодня, чтобы достичь той же цели? Решение: 1) 2) PV= Вывод: ежегодный взнос в банк составит 1987,3 долл. Единовременно положить в банк 11682,2 доллара. Задача № 10. Проект, требующий инвестиций в размере 160000 долл., предполагает получение годового дохода в размере 30000 долл. на протяжении 15 лет. Оценить целесообразность такой инвестиции, если коэффициент дисконтирования 15%. Решение: NPV= PI= R1=15% R2=18% NPV (r2) = IRR= Вывод: данный проект стоит принять т.к. чистый приведенный эффект больше 0, рентабельность больше 1, т.е. на каждый рубль затрат получаем больше прибыли. Внутренняя норма прибыльности больше цены капитала. Задача № 11. Предприятие инвестировало в проект 40 млн. руб. Ежегодные планируемые поступления от эксплуатации 20, 50, 100, 70 млн.руб. Ставка процента -55%. Произвести расчет аналитических коэффициентов и сделать выводы. Решение: R=55%
NPV= 20/1,55+50/1,552 +100/1,553+70/1,554-40=32,7 млн.руб.>0
PI=1,82>1 r2= 99% NPV2=39,83-40=-0,17
IRR= 55+[32,7/(39,83+0,17)]*44=90,97> r1 Проект вполне приемлем к реализации, т.к. чистый приведенный доход NPV>0, индекс рентабельности PI>1, что говорит о том, что с каждого рубля затрат получается 1,82 прибыли. Внутренняя норма прибыльности IRR превышает цену капитала. Резерв безопасности проекта 44% 12-15 Задача № 12. Анализируя два варианта накопления средств по схеме аннуитета пренумерандо, т.е. поступление денежных средств осуществляется в начале соответствующего временного интервала: План1: вносить на депозит 55 дол. Каждые пол года при условии, что банк начисляет 8% годовых с полугодовым начислением процентов; План2: делать ежегодный вклад в размере 1000 дол. на условиях 9% годовых при ежегодном начислении процентов. Какая сумма будет на счете через 12 лет при реализации каждого плана? Какой план более предпочтителен? Решение: FVpre = FVpst + (1+r)
План 1: FVpst= План 2: FVpst = Т.о. предпочтительнее к реализации второй план, т.к. FVpre2> FVpre1 Задача № 13. На вашем счете в банке 120 тыс. рублей. Банк платит 12,5% годовых. Вам предлагают войти всем капиталом в организацию совместного предприятия, обещая удвоение капитала через 5 лет. Принимать ли это предложение? Определить приемлемый уровень риска для участия в СП? Решение: Если оставить деньги в банке: FV=PV (1+r)n=120(1+0,125)5=216,2т.руб. 2) Если войти капиталом в совместное предприятие: FV=120*2=240т.руб. Следовательно выгоднее выбрать вариант входа в совместное предприятие. Приемлемый уровень риска:PV=
Задача № 14. Вы арендовали участок за 50000ден.ед. (единовременная выплата) на 5 лет; и можете выбрать один из двух вариантов: поставить мойку для автомобилей: оборудование стоит 80000ден.ед., ежегодный прогнозный приток составит 35000 ден.ед; сдать участок в субаренду за 15000ден.ед. в год. Какой вариант выгоднее для Вас? (Ставка процента 10%). Решение: 1) Первый вариант требует дополнительных инвестиций: IC=80000+50000=130000ден.ед. NPV= 2)NPV= Предпочтительнее второй вариант, т.к. чистый приведенных доход у второго варианта больше, по сравнению с первым. Задача № 15. Анализируются два варианта накопления средств по схеме аннуитета постнумерандо, то есть поступление денежных средств осуществляется в конце соответствующего временного интервала. План 1: вносить на депозит 500 долл. каждые полгода при условии, что банк начисляет 8% годовых с полугодовым начислением процентов. План 2: делать ежегодный вклад в размере 1000 долл. На условиях 9% годовых при ежегодном начислении процентов. Какая сумма будет на счете через 10 лет при реализации каждого плана? Какой план более предпочтителен? Изменится ли ваш выбор, если процентная ставка в плане 2 будет снижена до 8,5%? Решение FVpst = A*(((1+r)^n – 1)/r) План 1: FVpst = 500*(( (1+(0,08/2))^(10*2)-1 ) /(0,08/2)) = 14889,04 долл. План 2: FVpst = 1000*(( (1+0,09)^10-1 ) /0,09) = 15192,93 долл. При пониженной ставке в 8,5% в плане 2: FVpst = 1000*(( (1+0,085)^10-1 ) /0,085) = 14835,1 долл. Вывод: через 10 лет на счете банка в плане 1 будет лежать 14889,04 долл., а в плане 2 – 15192,93 долл. При ставках 8 и 9 процентов предпочтительнее проект 2, так как сумма на его счете выше. Однако, если снизить процентную ставку в плане 2 до 8,5%, то окажется предпочтительнее план 1. 16-17 Задача № 16. Проект, требующий инвестиций в размере 10000 долл. Будет генерировать доходы в течение 5 лет в сумме 2600 долл. Ежегодно. Стоит ли принять этот проект, если приемлемая ставка дисконтирования равна 9%. Рассчитать аналитические коэффициенты. Решение Рассчитаем дисконтированные показатели 1. NPV = PVpst – IC; PVpst = A*((1-(1+r)^(-n))/r) NPV = 2600*(1-(1+0,09)^(-5)/0,09) -10000 = 113,09 долл. NPV>0 – значит проект приемлем. 2. IRR = r1 + (NPV(r1)/(NPV(r1)-NPV(r2)))*(r2-r1) Пусть r2 = 15%. Тогда NPV = 2600*(1-(1+0,15)^(-5)/0,15) -10000 = -1284,4 долл. IRR = 9 + (113,09/(113,09+1284,4))*(15-9) = 9,5%. IRR>цены капитала (9,5>9) – значит проект выгоден. 3. PI = PVpst/IC; PI = 2600*(1-(1+0,09)^(-5)/0,09) /10000 = 1,01>1 – значит проект выгоден. Вывод: данный проект принимать не стоит, хотя рассчитанные аналитические коэффициенты показывают, что проект выгоден. Данный проект очень рискованный, потому что чистый приведенный доход очень маленький (всего 113,09 долл.), внутренняя норма доходности выше цены капитала лишь на 0,5%, а индекс прибыльности всего на 0,01 больше единицы. Задача № 17. Вы сдали в аренду на 10 лет участок земли. Арендатор предлагает вам выбрать один из 2 вариантов оплаты. 1: вы получаете немедленно 15 тыс. долл. плюс ежегодные поступления в размере 3000 долл. в течение 10 лет (схема постнумерандо). 2: вы получаете 4,5 тыс. дол. ежегодно в течение 10 лет (схема пренумерандо). Какой вариант предпочтительнее, если приемлемая норма прибыли составляет 8%. Каким должен быть платеж в варианте 2, чтобы оба варианта оказались равноправными? Решение
1) 2)
А = 3736,52 долл. Вывод: предпочтительнее вариант 2, так как доход арендодателя при 2 способе оплаты будет выше, чем при 1 способе. 18-19 Задача № 18. Величина требуемых инвестиций по проекту равна 18000 долл. предполагаемые доходы: в первый год -1500 долл., в последующие 8 лет – 3600 долл. ежегодно. Оцените целесообразность принятия проекта, если стоимость капитала 10%. Решение: ARR=
DPP=8лет + 703,36/1526,751=8,46лет NPV= PI=
R1=10%, R2=15%
NPV (r2)=
IRR= Вывод: данный проект стоит принять т.к. чистый приведенный эффект больше 0, рентабельность больше 1, т.е. на каждый рубль затрат получаем больше прибыли. Внутренняя норма прибыльности больше цены капитала. Задача № 19. К моменту выхода на пенсию, т.е. через 8 лет, г-н N хочет иметь на счете 30000 долл. Для этого он намерен делать ежегодный взнос в банк по схеме пренумерандо. Определите размер взноса, если банк предлагает 7% годовых. FVpre=FVpst*(1+r) FVpre=A* 30000=A* 30000=10,978*A A=2732,74 долл 20 Задача № 20. Величина инвестиции – 1 млн. руб; прогнозная оценка генерируемого по годам дохода (тыс. руб.): 344; 395; 393; 322. Стоит ли принять этот проект, если приемлемая ставка дисконтирования равна 9%? Рассчитать аналитические коэффициенты IC=1000 т.р. Денежный поток (т.р.): 344; 395; 393; 322 1) Коэффициент эффект-сти инвестиций: ARR = PN=(344+395+393+322)/4=363,5 т.р. ARR= ARR сравнивают с коэффициентом рентабельности авансированного капитала: Рав.кап-ла=П / IC= 363,5 / 1000=0,3635 или 36,35%<ARR, т.е. проект приемлем 2) Срок окупаемости: PP -1000 +344 = -656 +395 = -261 +393 = 132 РР=2 года + 261/(132+261) = 2,53 года 3) Дисконтированный срок окупаемости: DPP -1000 +344/1,09 = -684,4 +395/1,09 +393/1,09 +322/1,09 DPP=3 года + 48,47/(179,64+48,47) = 3,2 года DPP>PP, т.е. в течение 4-ёх лет доход перекроет инвестиции, т.е. проект приемлем 4) Чистый приведенный доход: NPV = NPV= 344/1,09 + 395/1,09 5) Индекс рентабельности инвестиций: PI = PI= (344/1,09 + 395/1,09
6) Внутр. норма прибыльности: IRR = r Пусть r IRR = 9+ Проверка: NPV(0,17) = -0,2 ≈ 0 IRR=17%>9%, т.е. проект приемлем Вывод: Т.о. все аналитические коэффициенты имеют приемлемые значения, и значит, проект стоит принять. 21-22 Задача № 21. Для ремонта системы отопления в квартире через 5 лет, по прогнозам специалистов, вам потребуется 2000 долл. Вы решили накопить необходимую сумму, вложив в настоящий момент 1000 долл. в банк под 18% годовых. Определить: 1) хватит ли накопленной суммы для ремонта; 2) размер взноса, достаточный для достижения необходимого результата 1) FV=PV*(1+r) 2) PV=FV/(1+r) Задача № 22. Сравните 2 проекта, если стоимость капитала 13% А: -20000 7000 7000 7000 7000 В: -25000 2500 5000 10000 20000 1) Коэффициент эффект-сти инвестиций: ARR = А: ARR= В: ARR= 2) Срок окупаемости: PP А: -20000 +7000 = -13000 +7000 = -6000 +7000 = 1000 РР=2 года + 6000/(1000+6000) = 2,86 года В: -25000 +2500 = -22500 +5000 = -17500 +10000 = -7500 +20000 = 12500 РР=3 года + 7500/(7500+12500)=3,375 года 3) Дисконтированный срок окупаемости: DPP А: -20000 +7000/1,13 = -13805,31 +7000/1,13 +7000/1,13 +7000/1,13 DPP=3 года + 3471,93/(3471,93+821,299) = 3,81 года DPP>PP, т.е. в течение 4-ёх лет доход перекроет инвестиции, т.е. проект приемлем В: -25000 +2500/1,13 = -22787,61 +5000/1,13 +10000/1,13 +20000/1,13 DPP=3 года + 11941,38/(11941,38+324,999)= 3,97 года DPP>PP, т.е. в течение 4-ёх лет доход перекроет инвестиции, т.е. проект приемлем 4) Чистый приведенный доход: NPV = А: NPV= А* В: NPV= 2500/1,13 + 5000/1,13 5) Индекс рентабельности инвестиций: PI = А: PI= 20821,299/20000 = 1,041>1, т.е. проект выгоден В: PI= 25324,999/25000 = 1,013>1, т.е. проект выгоден 6) Внутр. норма прибыльности: IRR = r А: Пусть r IRR = 13+ Проверка: NPV(0,15) ≈ 0 IRR=17%>9%, т.е. проект приемлем В: Пусть r IRR = 13+ Проверка: NPV(0,1347) ≈ 0 Вывод: Т.о. все аналитические коэффициенты имеют приемлемые значения как для проекта А, так и для проекта В, и значит, оба проекта целесообразны. Однако по всем показателям кроме ARR выгоднее проект А 23-24 Задача № 23. Вы имеете 20 тыс. руб. и хотели бы удвоить эту сумму через 5 лет. Каково минимальное приемлемое значение процентной ставки? PV=20000 т.р. FV=40000 т.р. n=5лет FV=PV*(1+r) 40000 = 20000*(1+r) (1+r) Задача № 24. Для фирмы затраты на капитал равны 12%. Она рассматривает два взаимоисключающих объекта (Х и У) со сроком жизни 10 лет и следующими характеристиками:
Решение
NPV1=150/1,12^1 +...+150/1,12^10 – 500 = 347,52 тыс. долл. + IP1 = 347,52/500 = 69,5 % - IRR1=12+(347,52/(347,52-(-9,66))) * (28-12)= 27,56 % - РР1=3+50/(50+100) = 3,33 года - DРР1= 4+44,39/(44,39+40,72)=4,52 года - Проект У NPV2=40/1,12^1 +... + 40/1,12^10 – 100 = 126 тыс. долл. - IP2= 126/100 = 126 % + IRR2 = 12 + (126/(126-(-1,25))*(39-12)) = 38,73 % + РР2 = 2+20/(20+20) = 2,5 года + DРР1 = 3+3,93/(3,93+21,49) = 3,15 года + Вывод: по проведенному расчету можно сделать вывод, что проект У выгоднее проекта Х, хотя чистый приведенный доход проекта Х больше, чем у У. Однако срок окупаемости, дисконтированный срок окупаемости, внутренняя норма доходности и индекс прибыльности у проекта У больше, чем у проекта Х. 25-28 Задача № 25. Г-н N хочет приобрести пенсионный контракт, по которому он мог бы получать ежегодно по 7000 долл. в течение оставшейся жизни. Страховая компания, используя таблицы смертности, оценила, что клиент сможет прожить 20 лет, и установила 6% годовых. Сколько нужно заплатить за контракт? Решение
Вывод: за контракт надо заплатить 80289,45 долл. Задача № 26. Предприниматель инвестировал 700000 долл. Определенная сумма будет ежегодно выплачиваться в течение 20лет исходя из ставки 15%годовых. Какую сумму ежегодно будет получать пред-ль? Решение PV=700000 r=15% FV=PV(1+r)=700000(1+0.15)=805000долл. Задача № 27. Приведены данные о 2 альт-х проектах: А: -20 40 В: -1000 1200. Рассчитайте IRR и NPV проектов, если стоимость источника 15%. Каков будет ваш выбор, если решение принимается на основании: 1)только критерия IRR; 2)только критерия NPV? Решение 1) r1=15% NPVa=(40/((1+0,15)^1))-20=14.78 r2=100% NPVa2=0 2) NPVb=(1200/((1+0.15)^1))-1000=43.5 r2=20% NPVb2=0 3)IRRa=15+(14.78/(14.78-0))*(100-15)=100% 4)IRRb=15+(43.5/(43.5-0))*(20-15)=20% Вывод: 1) Если принять решение на осн-ии IRR,то выгоднее проект А; 2) Если принять решение на осн-ии NPV,то выгоднее проект В; Задача № 28. Фирме предложено инвестировать 100 млн. руб. на срок 5 лет при условии возврата этой суммы частями (ежегодно по 20 млн. руб.). По истечении 5 лет будет выплачено вознаграждение в размере 35 млн. руб. Примет ли она это предложение, если можно депонировать деньги в банк из расчета 8% годовых, начисляемых ежеквартально. Решение. 1) Если депонировать эти средства в банк, то через 5 лет фирма получит: FV = PV*(1+r)n = 100 млн. *(1+0,08/4)5*4 = 148,59 млн. руб. 2) Если инвестировать эти средства, то: Будущая стоимость инвестированной суммы составит (стоимость постоянного аннуитета с потоками постнумерандо):
Т. о. через 5 лет фирма получит: 117,3 +35 = 152,3 млн. руб. Вывод: Для фирмы выгоднее вложить средства в инвестиционный проект, т. к. это принесет большую прибыль. 29-30 Задача № 29. На предприятии осуществлены реконструкция и техническое перевооружение производства, на проведение которых было израсходовано 5 млн. руб. В результате этого денежные поступления (чистая прибыль + амортизационные отчисления) по годам за расчетный период составили (в млн. руб.): 1,2; 1,8; 2,0; 2,5; 1,5. Ставка дисконта составляет 20%. Произвести расчет аналитических показателей и сделать выводы. Срок окупаемости определить с использованием различных методов. Решение. 1) Чистый приведенный доход:
2) Срок окупаемости: РР= - 5 млн. руб. + 1,2=-3,8 млн. руб. (1 год) + 1,8 = -2,0 (2 года) + 2,0 =0 (3 года) 3) Внутренняя норма доходности: r1 =20%; NPV(r1) = 0.22 млн. руб. r2 =25%; NPV(r2) = -0.35 млн. руб.
4) Индекс рентабельности инвестиций:
5) Дисконтированный срок окупаемости: -5 млн. руб. + 1,2/1,2 = - 4 млн. руб. (1 год) +1,8/1,22 = -2,75 (2 года) +2,0/1,23 = -1,59 (3 года) + 2,5/1,24 = -0,38 (4 года) + 1,5/1,25 = 0,22 (5 лет) DPP= 4 года + 0,38/(0,38+0,22) = 4,6 лет (4 года и 7 мес.) Вывод: Чистый приведенный доход от проведения указанных мероприятий составил 0,22 млн. руб., он больше нуля, что говорит об их выгодности. Внутренняя норма доходности проекта на 1,94% превышает ставку дисконта, что говорит о его малом «запасе прочности». Индекс доходности инвестиций больше 1, что т. ж. указывает на приемлемость проекта. Срок окупаемости проекта 3 года, однако этот показатель нельзя принимать в расчет, т. к. он не учитывает ценность денег во времени. Дисконтированный срок окупаемости же составляет 4,6 года, т. е. данный проект реконструкции окупается почти 5 лет. По всем рассчитанным показателям проект можно считать приемлемым, однако судить о выгодности его для предприятия можно только проанализировав данные о прибыли предприятия до модернизации производства. Задача № 30. Приведены данные о двух альтернативных проектах (тыс. руб.): А: -1000 700 800 В: -400 350 300 Рассчитайте дисконтированные критерии инвестиционного анализа, если стоимость источника 15%. Каков будет ваш выбор, если решение принимается на основании: а) только относительных показателей; б) только абсолютного показателя. Решение а) PI= PIА= PIВ= PIВ> PIА, значит проект В является более приемлемым. б) NPV= Если NPV>0, проект приемлем. NPVА= NPVВ= NPVА > NPVВ, отсюда следует, что проект а более приемлем. Т.обр., можно сделать вывод о том, что проект А более приемлем т.к. NPVА > NPVВ, даже при PIВ> PIА. 31-35 Задача № 31. За выполненную работу предприниматель должен получить 60 тыс. руб.Заказчик не имеет возможности рассчитаться в данный момент и предлагает отложить срок уплаты на 2 года, по истечении которых он обязуется выплатить70 тыс. руб. Выгодно ли предпринимателю, если приемлемая норма прибыли составляет 10%?. Какова минимальная ставка, которая делает подобные условия невыгодными для предпринимателя? Решение: FV=60*(1+0.1)^2=72.6 тыс. руб. Для предпринимателя не выгодно, т.к. он ему платит только 70 тыс. руб. Минимальная ставка которая делает подобные условия невыгодными: r=(FV-PV)/PV r=(72,6-60)/72.6=0,21 или 21% Задача № 32. Проект, требующий инвестиций в размере 150000 долл., предполагает получение годового дохода в размере 30000 долл. На протяжении 15 лет. По истечении этого срока в течение года будут проводиться работы по ликвидации последствий проекта, в результате чего в 16- году будет отток средств в сумме 10000 долл. Оцените целесообразность принятия проекта, если коэффициент дисконтирования 8%. Решение: PVpst=A*(1-(1+r)^-n)/r PVpst=30000*(1-(1+0.08)^-15)/0.08=256784.4 PV=10000/1.08^16=2918.9 NPV= PVpst-PV-IC NPV=256784.4-150000-2918.9= 103865.5 долл. Принятие проекта целесообразно т. к. NPV>0. Задача № 33 Вы имеете возможность ежегодно делать взнос в банк в размере 1000 долл. На условиях 12 % годовых, начисляемых раз в год. Какая сумма будет на счете через 10 лет, если взнос делается одной суммой в начале каждого года. Решение: FVpst =
Задача № 34 Ожидается, что проект, требующий инвестиции в размере 100 тыс. долл., будет генерировать доходы в течение 8 лет в сумме 30 тыс. долл. ежегодно. Приемлемая ставка дисконтирования равна 10 %. Рассматриваются два варианта: без учета риска и с учетом риска. В первом случае анализ проводится без какой-либо корректировки исходных данных. Во втором случае вводится поправка на риск к ставке дисконтирования в размере трех процентных пунктов. Стоит ли принять этот проект в каждом из приведенных вариантов? Решение: Без учета риска:
С учетом риска: 10 % + 3 % = 13 %
Проект можно принять и в первом и во втором случае, так как NPV > 0 в обоих случаях. Но выгоднее без учета риска, так как NPV здесь больше. Задача № 35 Преуспевающий предприниматель в знак уважения к своей школе намерен заключить договор со страховой компанией, согласно которому компания ежегодно будет выплачивать школе сумму в 5000 долл. От имени предпринимателя до тех пор, пока он жив. На основании таблиц смертности страховая компания определила, что этот процесс может продолжаться в течение 40 лет. Какой единовременный взнос должен сделать предприниматель, если приемлемая норма прибыли равна 5%. Решение А=5000 долл n=5 лет r=5% PVpre=A*1-(1+r)^-n*(1+r)/r=5000*(1-(1+0.05)^-40)*(1+0,05)/0,05=90084,75 долл 36-37 Задача № 36 Инвестор вкладывает в проект 12 млн. долл. Планируемые ежегодные поступления составят: 4, 6, 8, 3 млн. долл. Ставка процента равна 10 %. Произвести расчет аналитических коэффициентов и сделать выводы. Решение:
При r2 = 20 % NPV = 11,32-12 = -0,68 млн.долл.
или Решение Денежный поток, млн. долл: 4; 6;8;3; Дисконтир. денежн. Поток,млн.долл: 4/1,1^1=3,64; 6/1,1^2=4,98; 6; 2,04 NPV=3.64+4.98+6+2.04-12=4.66 PI=(3,64+4,98+6+2,04)/12=1.39>1 Tок=2.25 года Пусть r2=30%, тогда Дисконтир. денежн. Поток,млн. долл: 4/1,3^1=3,08; 6/1,3^2=3,54;3,68;1,05 NPV(r2)=3.08+3.54+3.68+1.05-12=-0.65 млн. долл IRR=10%+4.66/(4.6+0.65)*(30-10)=27.56% Инвестиции в данный проект являются экономически целесообразными, поскольку принесут инвестору прибыль в размере 4.66 млн. долл, IRR значительно превышает цену капитала, а PI>1, что свидетельствует о значительном резерве безопасности. Задача № 37 Имеются данные о двух проектах (тыс. долл.): А: -10 000 6 000 6 000 2 000 В: -10 000 5 000 5 000 5 000 Проанализировать проекты, рассчитав абсолютные и относительные аналитические критерии, полагая, что стоимость капитала составляет 12 %. Решение:
NPV > 0, PI > 1
Проект В выгоднее, так как NPVb > NPVa и PIb > PIa.
38-40 Задача № 38. Предприятие получило кредит на один год в размере 10 млн руб. с условием возврата 16 млн руб. Рассчитайте процентную и учетную ставки. Решение: r = r = d = Задача № 39 Вы выбираете место работы. Предлагается одинаковая сумма зарплаты (1200 ден. ед.), но с разными графиками выплат: 1) аванс в январе (600 ден.ед.), выплата «п
|


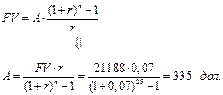
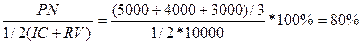
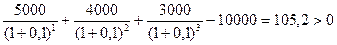

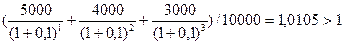

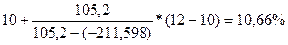
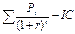
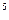 - 370 = 31,88 >0, т.е. проект выгоден
- 370 = 31,88 >0, т.е. проект выгоден + 60/1,2
+ 60/1,2 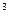 + 60/1,2
+ 60/1,2 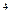 - 240 = -84,68 < 0, т.е. проект не выгоден
- 240 = -84,68 < 0, т.е. проект не выгоден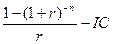 =100*
=100* 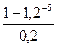 - 263,5 = 35,56 >0, т.е. проект выгоден
- 263,5 = 35,56 >0, т.е. проект выгоден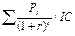
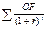 =370/1,2
=370/1,2  =370
=370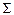 IF
IF 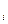 *(1+r)
*(1+r)  =0*1,2
=0*1,2 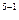 +…+1000*1,2
+…+1000*1,2 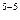 =1000
=1000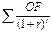 =240/1,2
=240/1,2 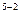 +60*1,2
+60*1,2 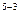 +60*1,2
+60*1,2 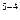 =386,496
=386,496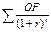 =263,5/1,2
=263,5/1,2 
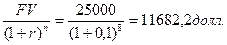
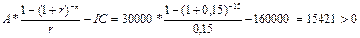

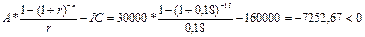
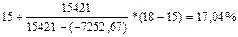
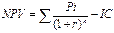
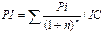
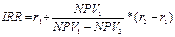
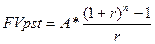
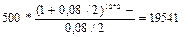 FVpre= 20322, 95 дол.
FVpre= 20322, 95 дол.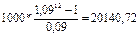 FVpre=21953,72 дол.
FVpre=21953,72 дол.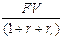 ; 120=
; 120=  , отсюда найдем rr = 2,5%/
, отсюда найдем rr = 2,5%/
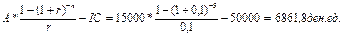
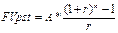
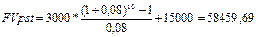 долл.
долл.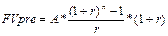
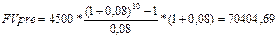 долл.
долл.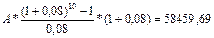
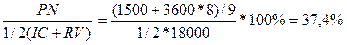
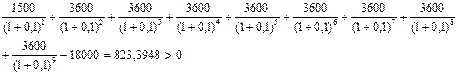
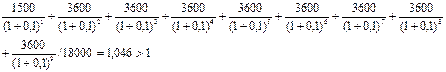
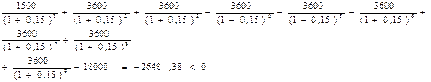

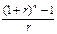 *(1+r)
*(1+r)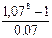 *1.07
*1.07
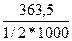 *100%=72.7%
*100%=72.7%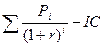
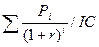
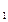 +
+ 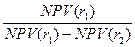 *(r
*(r  -r
-r 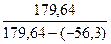 *(20-9) = 17%>9%, т.е. проект приемлем
*(20-9) = 17%>9%, т.е. проект приемлем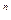 = 1000*(1+0,18)
= 1000*(1+0,18) 
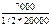 *100%=70%
*100%=70%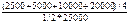 *100%=75%
*100%=75%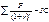
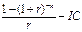 =7000*
=7000* 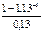 - 20000 = 821,299 >0, т.е. проект выгоден
- 20000 = 821,299 >0, т.е. проект выгоден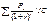
 *(r
*(r 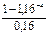 - 20000 =-412,74
- 20000 =-412,74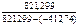 *(16-13) = 15%>13%, т.е. проект приемлем
*(16-13) = 15%>13%, т.е. проект приемлем *(14-13) = 13,47 %>9%, т.е. проект приемлем
*(14-13) = 13,47 %>9%, т.е. проект приемлем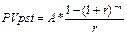
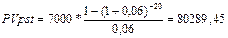 долл.
долл.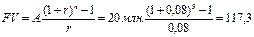 млн. руб.
млн. руб.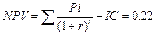 млн. руб.
млн. руб.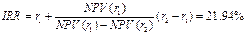
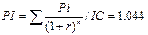
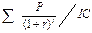
 = (608,696 + 606,061)/1000 = 1,215
= (608,696 + 606,061)/1000 = 1,215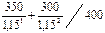 = (304,34 + 227,27)/400 = 1,33
= (304,34 + 227,27)/400 = 1,33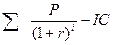
 213, 61
213, 61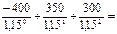 131,19
131,19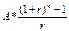 =
= 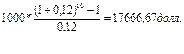

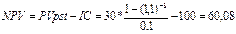

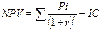
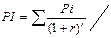 IC
IC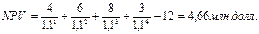
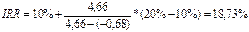
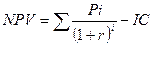
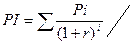 IC
IC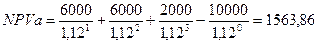 NPVa > 0, проект приемлем
NPVa > 0, проект приемлем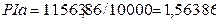 PI > 1, проект приемлем
PI > 1, проект приемлем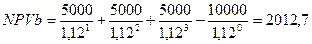 NPV > 0, проект приемлем
NPV > 0, проект приемлем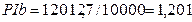 PI > 1, проект приемлем
PI > 1, проект приемлем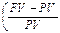 ; FV = 16млн. PV= 10млн.
; FV = 16млн. PV= 10млн.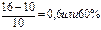
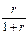 ; d=
; d=