Постановка задачи
Параболой называется множество точек плоскости, равноудаленных от заданной точки
Каноническое уравнение параболы, симметричной относительно оси Ох (рис. 4):
Каноническое уравнение параболы, симметричной относительно оси Оу (рис. 5):
В обоих случаях вершина параболы, то есть точка, которая находится на оси симметрии, находится в начале координат. Парабола Парабола Директориальное свойство кривых второго порядка: отношения расстояний от данной точки кривой к его фокусу иd к соответствующей директрисе есть величина постоянная, которая равняется эксцентриситету кривой:
Лабораторная работа № 82 Определение фокусных расстояний собирающей и рассеивающей линз Цель работы: На основании уравнения тонкой линзы экспериментально определить фокусные расстояния собирающей и рассеивающей линз, по предложенной методике научиться строить изображения предметов в тонких линзах. Оборудование: Оптическая скамья, осветитель со шкалой, рейтеры для крепления линз, экран, источник питания, собирающая и рассеивающая линзы.
Постановка задачи
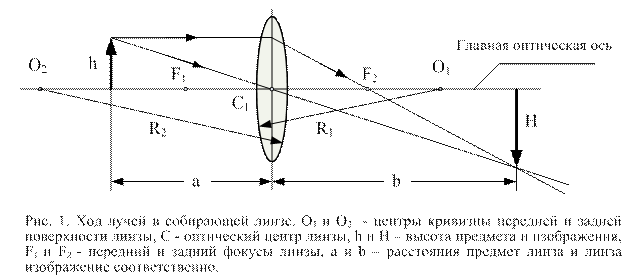
В основе рассматриваемых в данной работе методов экспериментального определения фокусных расстояний тонких линз лежит уравнение тонкой линзы, которое с учетом правила знаков для линз любой формы (двояковыпуклых, двояковогнутых, плосковыпуклых и др.) и ограниченных сферическими поверхностями имеют вид:
где а и b - расстояния от оптического центра линзы до предмета и изображения соответственно, n12 - относительный показатель преломления материала линзы, R1 и R2 радиусы кривизны передней и задней поверхностей линзы (для плоской поверхности R = ¥). Вывод формулы тонкой линзы смотрите, например, в пособиях [1 – 3]. Напоминаем правило знаков для отрезков, используемое при выводе формулы (1): отрезки, отсчитываемые от оптического центра вправо, (в направлении распространения светового луча) принимаются положительными, влево от оптического центра (в направлении противоположном распространению светового луча) – отрицательными. Это правило подобно правилу определения знаков координат при выбранных положительных направлениях осей координат. Так для примера на рис.1 радиус кривизны R2 при подстановке в формулу (1) берется со знаком "-",а R1 со знаком "+". Отметим также, что номер радиуса кривизны поверхности линзы определяется порядком их следования в направлении движения луча от предмета к линзе. На рис.1 представлен ход лучей в собирающей линзе и указаны величины, входящие в формулу (1). В формуле (1) величина (n12 -1)(1/R2 -1/R1) называется оптической силой линзы и обозначается буквой D, величина ей обратная определяет главное фокусное расстояние (или просто фокусное расстояние) F:
Главным фокусным расстоянием линзы называют расстояние от оптического центра линзы до главного фокуса – точки на главной оптической оси, в которой получается изображение бесконечно удаленной светящейся точки, также расположенной на главной оптической оси. Определение других понятий, касающихся преломления света в линзах, см. [1,2].
С учетом правила знаков формула (1) для случая представленного на рис.1 имеет вид:
где, а, b, R1 и R2 - уже взяты по модулю. После очевидных преобразований - умножения на "-1" и подстановки выражения (2) формула (1) примет более лаконичный вид:
Из формулы (4) или (1), а также рис. 1 видно, что величины а, b, F, h, H связаны однозначно. Поэтому, экспериментально определяя величины а, b, h и H и используя выражение (4) можно определить фокусное расстояние собирающей линзы по формуле:
Определение фокусного расстояния рассеивающей линзы на основе экспериментального измерения а, b, h и H требует иного способа, поскольку одна рассеивающая линза не позволяет получить действительного изображения предмета на экране. Рассмотрим методику определения фокусного расстояния рассеивающей линзы. Пусть с помощью собирающей линзы получено изображение А" точечного предмета А, см. рис.2. При построении изображения точки А мы воспользовались понятиями побочной оптической оси и побочного фокуса. Любая прямая проходящая через оптический центр линзы (точка С рис. 1) называется оптической осью, если она также проходит и через центры кривизны поверхностей, ее называют главной оптической осью. Совокупности лучей параллельных главной или побочной оптической оси пересекаются в одной точке, называемой соответственно главным и побочным фокусами линзы. Для построения точки А, рис.2, взято два луча 1 и 2. Луч 2 проходит через собирающую линзу не отклоняясь. Ход луча 1 через линзу определяем с помощью побочной оптической оси Если теперь на пути лучей, прошедших линзу L1, поставить рассеивающую линзу L2 так, чтобы расстояние С2А" было меньше ее фокусного расстояния, то действительное изображение предмета А удалится и окажется в точке А' (рис.2).
Вследствие принципа обратимости световых лучей в оптических системах можно рассматривать лучи света как бы распространяющиеся из точки А' влево. Тогда А" будет мнимым изображением точки А'. Введем обозначения: А'С2 = а; А"С2 = b. Тогда формула (1) для рассеивающей линзы L2 с учетом правила знаков при указанном на рис.2 направлении распространения света (а > 0, b > 0, F < 0 т.к. фокус линзы L2 мнимый) примет вид:
Откуда имеем для F:
|

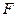 (фокуса) и заданной прямой (директрисы).
(фокуса) и заданной прямой (директрисы).
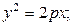
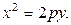
 имеет фокус
имеет фокус 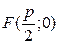 и директрису
и директрису 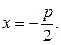
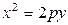 имеет фокус
имеет фокус 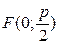 и директрису
и директрису 

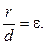
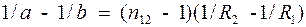 . (1)
. (1)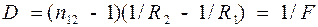 (2)
(2)
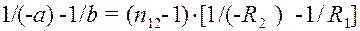 , (3)
, (3)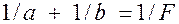 (4)
(4)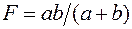 (5)
(5)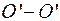 . Она пересекает фокальную плоскость Ф1 в точке
. Она пересекает фокальную плоскость Ф1 в точке  . Луч 1 после преломления в собирающей линзе проходит через этот побочный фокус и пересекается с лучом 1 в точке
. Луч 1 после преломления в собирающей линзе проходит через этот побочный фокус и пересекается с лучом 1 в точке 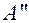 . Эта точка и является изображением точки А.
. Эта точка и является изображением точки А.
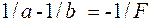 . (5)
. (5)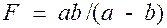 . (6)
. (6)


