Из условия (1) следует, что резонанса можно достичь, изменяя индуктивность, емкость и частоту входного сигнала ¦.Резонанс напряжений называется такой пассивной электрической цепи переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений, при котором входное реактивное сопротивление равно нулю. При резонансе напряжений напряжение на входе цепи совпадает по фазе с током, т.е.
j = yu - yi =0
Условие фазового резонанса через параметры последовательного контура записывается в виде:
хL=xC или
 (1)
Значения параметров определяются по формулам:
Явление резонанса напряжений характеризуется следующим рядом соотношений. 1. Полное сопротивление цепи
2. Сопротивление цепи минимально, ток в момент резонанса максимален, что следует из закона Ома
3. Сопротивление каждого из реактивных элементов при резонансе хL=xC не зависит от частоты, называется характеристическим сопротивлением цепи (волновое сопротивление) xCрез = хLрез; 4. Величины напряжений на активном, индуктивном, емкостном сопротивлениях могут быть определены Ua=I×R; UL=I×xL; Uc=I×xC, т.к. хL=xC, то UL=Uc=rI. Векторная диаграмма тока и напряжений приведена на рис.1. 5. Отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи, при резонансе называют добротностью контура или коэффициентом резонанса.
Коэффициент резонанса показывает во сколько раз напряжение на индуктивности или емкости при резонансе больше, чем напряжение приложенное к цепи.
Величина, обратная добротности, называется затуханием цепи
6. Отношение активной мощности к полной, равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности:
Коэффициент мощности при резонансе напряжений равен 1.
Активная мощность равна полной мощности: P=S. На рисунке 1 приведены графики мгновенных значений тока и напряжений.
Рис. 2 Векторная диаграмма тока и напряжений в момент резонанса. В рассматриваемой лабораторной работе явление резонанса напряжений получают изменением индуктивности, емкости, частоты входного сигнала.
|
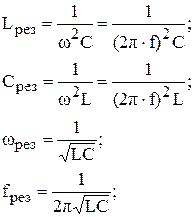
, т.к. х=0; комплекс полного сопротивления
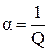
Рис. 1 Графики мгновенных значений тока и напряжений.
