I.3 Второстепенная балка
Методические указания. Схема армирования второстепенной балки сварными каркасами должна приниматься согласно рис.3. Не допускается подбирать продольную арматуру со стержнями разного диаметра. Поперечная рабочая арматура при диаметре стержней до 6 мм принимается класса Вр-I, а при больших диаметрах класса А-I.
Решение. Вычисляем расчетный пролет для первого (крайнего) пролета,который равен расстоянию от оси опоры на стене до грани главной балки (рис.3) l01=l-c/2-b/2=5600-250/2-250/2=5350 мм. Определим расчетную нагрузку на 1 пог. м второстепенной балки, собираемую с грузовой полосы шириной равной максимальному расстоянию между осями второстепенных балок (2,1м) Постоянная нагрузка: - от веса плиты и пола 3,64*2,4=8,74 кН/м -от веса ребра балки 0,25(0,45-0,08)*25*1,1=12,54 кН/м Итого g=8,74+2,54=11,28 кН/м Временная нагрузка: V=12*2,4=28,8 кН/м Итого с учетом коэффициента надежности по назначению здания q=(g+v)*gn=(11,28+28,80)*1=40,08 кН/м. Определим изгибающие моменты с учетом перераспределения усилий - в первом пролете М=q*l201/11=40,08*5,352/11=104,30 кН*м; - на первой промежуточной опоре М=q*l201/14=40,08*5,352/14=81,90 кН*м. Максимальная поперечная сила (на первой промежуточной опоре слева) равна Q=0,6*q*l01=0,6*40,08*5,35=129 кН. Согласно задания продольная рабочая арматура для второстепенной балки класса А-III(RS=365 МПа). Проверим правильность предварительного назначения высоты сечения второстепенной балки: h0³ или h=h0+a=331,00+35=366,0< 400 мм, т.е. увеличивать высоту сечения не требуется. Выполним расчеты прочности сечений, нормальных к продольной оси балки, на действие изгибающих моментов. Сечение в 1-ом пролете М= 104,3кН*м. Определим расчетную ширину полки таврового сечения согласно [2,п.3.16]: при h¢f/h=80/450=1,75>0,1 и 2*1/6*l01+b=2*1/6*5350+250=2033,33<2300мм принимаем b¢f=2033,0мм. Вычислим h0=h-a=450-30=420мм. Так как Rb*b*h¢f*(h0-0,5*h¢f)=10,35*2033*80*(420-40)=639,7 кН*м>M=104,3кН*м, граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b=b¢f=2033 мм. Вычислим am=M/(Rb*b*h20)=104,3*106/(10,35*2033*4202)=0,028<aR . По приложению I при am=0,028 находим z=0,987, тогда Аs=M/(Rs*z*h0)=104,3*106/(280*0,987*420)=898,58мм2. Принимаем 2Æ25 А-I (Аs=982 мм2). М=81,9 h0=450-35=415 am=81,9*106/(280*0,998*415)=7062мм2. Принимаем 5Æ14 А- I I I (Аs=769 мм2). 25/4
Выполним расчет прочности наиболее опасного сечения балки на действие поперечной силы у опоры слева. По приложению 2 из условия сварки принимаем поперечные стержни диаметром 5 мм класса Вр-I (Rsw=260 МПа, Еs=170000 МПа), число каркасов-2 (Аs=39,2 мм2). Назначаем максимально допустимый шаг поперечных стержней S=150 мм согласно требованиям [2, п.5.27]. Поперечная сила на опоре Qmax=92,127 кН, фактическая равномерно распределенная нагрузка q1=28,7 кН/м, бетон тяжелый класса В20, Rb=10,35 МПа, Rbt=0,81 МПа, Еb=24,0*103 МПа. По условию (72) проверим прочность наклонной полосы [2]. определяем коэффициенты jw1 и jb1: mw=Asw/(b*S)=39,2/(200*150)=0,0013; a=Es/Eb=170000/24000=7,39; отсюда jw1=1+5a*mw=1+5*8,33*0,0013=1,05<1,3; для тяжелого бетона b=0,01; jb1=1-b*Rb=1-0,01*10,35=0,990. Тогда 0,3*jw1*jb1*Rb*b*h0=0,3*1,05*0,990*10,35*200*370=216,288 кН>Qmax=92,127 кН, т. е. прочность наклонной полосы обеспечена. По условию (75) проверим прочность наклонного сечения по поперечной силе [2]. Определим величины Мb и qsw.: jb2=2; т.к. bf¢-b=1750-200=1550мм>3hf¢=3*70=210ьмм, принимаем bf¢-b=210мм, тогда jf=0,75*(bf¢¢-b)*hf¢/(b*h0)=0,75*210*70*/(200*370)=0,148<0,5; Мb=jb2*(1+jf)*Rbt*b*h02=2*(1+0,148)*0,675*3702*200=42,43кН/м; qsw=Rsw*Asw/S=260*39,2/150=67,9 кН/м Определим значение Qb, min, принимая jb3=0,6: Qb, min=jb3*(1+jf)*Rbt*b*ho=0,6*1,05*0,81*200*370=37,76 кН. Поскольку Qb, min/(2*ho)=37,76/2*0,37=51,03кН/м<qsw=67,9кН/м, следовательно значение Мb не корректируем. Согласно [3.п.3.32] определяем длину проекции опасного наклонного сечения С. Поскольку 0,56*qsw=0,56*67,9=38кН/м>q1=28,7кН/м, значение С определяем только по формуле С= Тогда Qb=Mb/C=42,43/1,23=34,5>Qb, min =37,76Н; Q=Qmax-q1*C=92,127-28,7*1,23=56,83кН. Длина проекции наклонной трещины равна Со= Поскольку Со=0,625<2*ho=2*0,37=0,74м, принимаем Со=0,625, тогда Qsw=qsw*Co=67,9*0,625=42,44кН. Проверим условие [2,формула(75)]: Qb+Qsw=37,76+42,44=80,19кН>Q=56,83Н, т.е. прочность наклонного сечения по поперечной силе обеспечена.
|


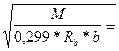


 7 возьмем принимаем арматуру К-7Æ8
7 возьмем принимаем арматуру К-7Æ8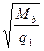 =1,5м. Поскольку С=1,23>(jb2/jb3)*ho=(2/0,6)*0,37=1,23м, принимаем С=1,23м.
=1,5м. Поскольку С=1,23>(jb2/jb3)*ho=(2/0,6)*0,37=1,23м, принимаем С=1,23м. =0,625м.
=0,625м.


