Проектирование неразрезного ригеля.

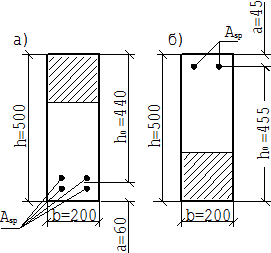
Методические указания. Неразрезной ригель многопролетного перекрытия представляет собой элемент рамной конструкции. При свободном опирании концов ригеля на наружные стены и равных пролетах ригель можно рассматривать как неразрезную балку. При этом возможен учет пластических деформаций, приводящих к пере­распределению и выравниванию изгибающих моментов между от­дельными сечениями.

Назначаем предварительные размеры поперечного се­чения ригеля.

Высота сечения h=600 мм. Ширина сечения ригеля b=250 мм.

Вычисляем расчетную нагрузку на 1 м длины ригеля. Нагрузка на ригеле от многопустотных плит считается равномерно распределен­ной. Ширина грузовой полосы на ригель равна шагу колонн в про­дольном направлении здания 5,6 м.

Постоянная нагрузка на ригель будет равна:

-от перекрытия

(с учетом коэффициента надежности по назначе­нию здания g_n =1) 3,97*5,6*1=22,23 кН/м;

-от веса ригеля (сечение 0,25õ0,6 м, плотность железобетона r=25 кН/м³, с учетом коэффициентов надежности g_f=1,1 и g_n=1) 0,25*0,7*25*1,1*0,955=4,825 кН/м.

Итого: g=22,23+4,825=27,0425 кН/м.

Временная нагрузка (с учетом g_n=1) V=12*5,6=67,2 кН/м.

Полная нагрузка q=27,0425+67,2=94,243 кН/м.

Характеристики бетона и арматуры для ригеля.
Бетон тяжелый, класса В25, g_b2 =0,9 (при влажности 50 %), R_b= 14,5*0,9=13,05 МПа; R_bt=1,05*0,9=0,945 МПа; E_b=27000 МПа.

Продольная рабочая арматура класса А-III R_s =365 МПа E_s =200000 МПа.

По приложению 2 для элемента из бетона класса В25 с арматурой класса А-III при g_b2 =0,9 находим a_R= 0,422 и x_R=0,604

Перераспределяем опорный момент в пролет, учитывая пластические свойства бетона

0,3 М_оп.max=0.3*260,65=78,195 тогда М_пр,=78,37+78.195=156,56 но так как этот момент меньше чем момент от 1+2 сочетания то М_пр,мах=218,80кН*м.

М_оп.max=260,65-78,195=182,455кН*м.

Уточним размеры поперечного сечения ригеля B*H=20*50см.

Расчет прочности ригеля по сечениям, нормальным к продоль­ной оси. Принимаем схему армирования ригеля согласно рис.

Сечение в пролете (рис.5 а),M=218,80 кНм,h₀=440мм.

Подбор продольной арматуры производим согласно [3 п. 3.18].

Вычисляем a_m=M/(R_bbh²₀)=218,80*10⁶/(17*200*440²)=0,27<a_R=0,41, следовательно, сжатая арматура не требуется. По приложению I при a_m=0,27 находим z=0,842, тогда требуемую площадь растянутой арматуры определим по формуле

A_S=M/(R_Sz h₀)=218,80*10⁶*/(365*0,842*440=1618,3мм².Принима­ем 4Æ25 мм, с A_s =1963мм².

 

 

Рис.5 К подбору продольной арматуры в ригеле: а- сечение в пролете, б- сечение на опоре

 

Сечение на опоре (рис.5 б), М = 182,45 кН*м h₀=455 мм
a_m=M/(R_bbh²₀)=182,45*10⁶/17*200*455²=0,28<a_R=0,41 z =0,835 тогда A_S=182,45*10⁶/(365*0,835*455)=1315 мм².

Принимаем 2 Æ32 мм. A-III (A_s=1609 мм².)

Монтажную продольную арматуру принимаем 2Æ12 A-III (A_s=226 мм²)

Расчет прочности ригеля по сечениям, наклонным к продольной оси.

Q_max=204,93 кН, q=54,41 кН/м

Определим требуемую интенсивность поперечных стержней из арматуры класса А-I (R_sw=175МПа; E_s=210000 МПа.) принимая в опорном сечении h₀= 462 мм.

Рис.6. К расчету прочности ригеля по наклонным сечениям.

при j_f=0 и j_b2=2,0 получим

М_b=j_b2*R _bt*b*h²₀=2*1,2*200*462²=81,48 кН*м.

Cогласно п.32[3] Q_b1=2 2 =133,17 кН. Так как Q_b1/0,6=221,94> Q_max=204,93кН, то требуемую интенсивность поперечных стержней определим по формуле

q_sw= кН/м.

Поскольку кН/м >q_SW=74,44кН/м

то принимаем q_sw=87,09 кН/м.

Проверяем условие [3, формула (57)] Q_b,min=j_b3R_btbh₀=0,6*1,2*200*462=59,33 кН; так как q_SW=87,09кН/м> Q_b,min/2h₀=59,33/(2*0,462)=72 кН/м,

то не корректируем значение q_SW

Согласно п. [2.5.27], шаг S₁ у опоры должен быть не более h/3=500/3=166 мм, а в пролете 3/4h=375 мм. Принимаем шаг поперечных стержней у опоры S₁=160 мм, а в пролете S₂=375 мм, отсюдa A_sw= q_SW* S₁/R_sw=87.09*160/175=79.63мм. принимаем в поперечном сечении два поперечных стер­жня диаметром по 8 мм с учетом диаметра продольной арматуры (A_sw=101 мм²).

Таким образом, принятая интенсивность поперечных стержней у опоры и в пролете будет соответственно равна:

q_sw1=R_swA_sw/S₁= 175*101/160=110,47 Н/мм; q_sw2= R_swA_sw/S₂= 175*101/375=47,13kН/мм.

Проверим условие [3,57]. Так как q_sw1= 110,47 >Q_{b, min}/2*h₀=72 кН, а q_sw2=47,13кН/м>

Q_{b, min}/2*h₀=72 кН то для вычисления l₁ корректируем значения М_b и Q_{b, min}

М_b=2* h₀² *q_sw2*j_b2/j_b3=2*462²*47,13*2/0,6=129,45кН*м.

Q_{b, min}=2* h₀*q_sw2=2*0,462*47,13=38,84кН.

Вычисляем c₀₁= = =1,08м. >2* h₀=0,824м.Þ c₀₁=0,824м.

Поскольку q₁= 54,41 кН < q_sw1- q_sw2=63,34 кН/м, Q_{b, min}+ q_sw2* c₀₁=38,84+47,13*0,824=77,68 > Q_{b, min}=59,33кН

то l₁ вычисляем по формуле
l₁=(((Q_max -(Q_{b, min}+ q_sw2* c₀₁))/ q₁)- c₀₁=((204,93-77,68)/54,41)-0,824=1,5 м.

Тогда L₁= l₁+ 0,2 =1,5+0,2=1,7м = (1/4)*6,8=(1/4)*6,8=1,7 м

Принимаем L₁=1,7 ì.

 

Проверяем прочность по наклонной полосе ригеля между на­клонными трещинами:

m_w=A_sw/(bs)=101/(200*160)=0,0032 a=E_s/E_b=200000/29000=6,9;
j_w1=1+5 am_w=1+5*6,9*0,0032=1,11<1,3;
j_b1=1-bR_b= 1-0,01*17=0,83; тогда 0,3j_w1j_b1R_bbh₀=0,3*1,11*0,83*17*200*462=387,167 кН >
Q_max =204,93кН следовательно, прочность наклонной полосы обеспечена.

 

Построение эпюры материалов выполняем с целью рационально­го конструирования продольной арматуры ригеля в соответствии с огибающей эпюрой изгибающих моментов

Определяем изгибающие моменты, воспринимаемые в расчетных сечениях, по фактически принятой арматуре.

Сечение в пролете с продольной арматурой 2Æ25 мм, A_s=982мм²; x=R_s A_s/(R_bb)= 365*982/(17*200)=105,42 мм; x=x/h₀=105,42/462,5=0,256 < x_R= 0,59;

тогда М=R_s A_s (h₀-0.5x)=365*982(462,5-0,5*105,42)=146,88 кН*м.

Сечение в пролете с продольной арматурой 4Æ25 мм A_s=1963 мм².
x=R_s A_s/(R_bb)=365*1963/17*200=210,73мм,
тогда M= R_s A_s (h₀-0.5x)=365*1963*(437,5-0,5*210,73)=237,973 кН*м..

Сечение в пролете с арматурой в верхней зоне 2Æ12 мм А_s=226 мм²; x=R_s A_s/(R_bb)=365*226/17*200= 24,26 мм;
M= R_s A_s (h₀-0.5x)= 365*226(482-0,5*24,26)=38,76 кН*м.

Сечение у опоры с арматурой в верхней растянутой зоне 2Æ32 мм, А_s=1609 мм²; x=R_s A_s/(R_bb)=365*1609/17*200=172,73 мм.
М= R_s A_s (h₀-0.5x)=365*1609(458-0,5*172,73)=218,256 кН*м.

Пользуясь полученными значениями изгибающих моментов, гра­фическим способом находим точки теоретического обрыва стержней и соответствующие им значения поперечных сил.

Вычисляем необходимую длину анкеровки обрываемых стержней для обеспечения прочности наклонных сечений на действие изгиба­ющих моментов в соответствии с[3 п. 3.46].

Для нижней арматуры по эпюре Q графическим способом находим поперечную силу в точке теоретического обрыва стержней диамет­ром 25 мм Q=82 кН, тогда требуемая длина анкеровки будет равна w₁=Q/(2q _sw)+5d=82*10³/(2*110,47)+5*25= 496.14мм =50 см.

Для верхней арматуры у опоры диаметром 32 мм при Q=43 кН соответственно получим
w_b= Q/(2q _sw)+5d=43*10³/(2*110,47)+5*32=352,89см.

 

 

 

V этап