| речь соответствует норме
| полная коррекция всех компонентов речи по первичному речевому заключению (при поступлении) в соответствии со сроками коррекции
|
| значительное улучшение речи
| А) недостаточная коррекция одного - двух компонентов языка по первичному речевому заключению из-за сокращения сроков коррекции;
Б) незаконченность этапов коррекции речи по объективным причинам
|
| без значительного улучшения речи
| А) при отсутствии положительной динамики коррекции всех компонентов языка из-за несоответствия тяжести речевого дефекта и сроков коррекции;
Б) при неадекватности коррекционно-развивающего маршрута
|
* Для коррекционных ДОУ
Действия над комплексными числами в алгебраической форме
Пусть заданы два комплексных числа: z1=a1+b1·i и z2=a2+b2·i, тогда:
| Сумма
z = z1 + z2
| z = z1 + z2=
= (а1+а2)+(b1+ b2) ·i
| 
|
| Разность
z = z1 - z2
| z = z1 - z2=
=(а1-а2)+(b1- b2) ·i
| 
|
Модуль разности

| 
| Изображает расстояние между точками z1 и z2.
|
Произведение

| 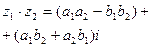
| Выполняют по правилу умножения многочленов, причем i2=-1
|
Произведение
комплексно-спряженных
z1 = a + b·i
 = a - b·i = a - b·i
|  . .
| Произведение комплексно - спряженных чисел равно сумме квадратов действительной и мнимой части комплексного числа.
|
Частное

| 
| Числитель и знаменатель умножены на число, комплексно-спряженное к знаменателю.
|
Действия над комплексными числами в тригонометрической форме
Пусть задано два комплексных числа: z1=r1(cosφ+i·sinφ),
z2=r2(cosφ+i·sinφ)
| Произведение
z = z1 · z2
| 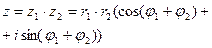
| При умножении модули перемножают, а аргументы складывают
|
Частное

| 
| При делении модули делят, а аргументы отнимают.
|
| zn
| zn = rn(cos n·φ+i·sin n·φ)
| При возведении в степень, модуль возводят в степень, а аргументы умножают на показатель степени.
|
| Формула Муавра
| (cosφ+i·sinφ)n =
= cos n·φ+i·sin n·φ)
| r = 1
|
Корень n- й степени из числа z0
 где
где 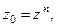
| 
| Точки, которые соответствуют разным значениям корня, размещают в вершинах правильного n - угольника с центром в точке 0 и получают полярные координаты:
 . .
|
Действия над комплексными числами в показательной форме
z1= r1· еiφ1, z2= r2· еiφ2, е=2,7182818… - иррациональное число
.
Формула Эйлера: еiφ=(cosφ+i·sinφ).
Следствия: 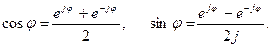
| Произведение
z = z1 · z2
| z = z1 · z2 = r1· r2·  . .
|
Частное
 . .
|  . .
|
| Возведение в степень.
| 
|
| Извлечение корня n -й степени
| 
|






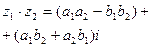
 = a - b·i
= a - b·i
 .
.


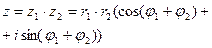


 где
где 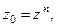

 .
.
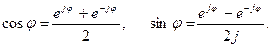
 .
.
 .
.





