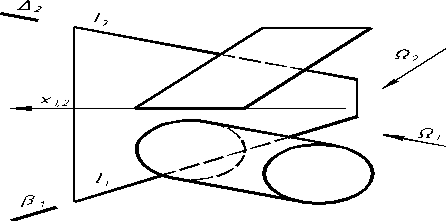
Для побудови точок перетину прямої l з циліндром доцільно скористатися
a) [ ] косокутним паралельним проекціюванням на П1 за напрямком Ω; b) [ ] косокутним паралельним проекціюванням на П2 за напрямком Ω; c) [ ] допоміжною січною площиною β; d) [ ] допоміжною січною площиною Δ. 245. Для побудови точок перетину прямої l з конусом доцільно скористатися:
a) [ ] центральним проекціюванням на П2 з центром S; b) [ ] центральним проекціюванням на П1 з центром S c) [ ] допоміжною січною площиною Δ; d) [ ] допоміжною січною площиною β. 246. Точками перетину прямої l з пірамідою будуть:
247. Якщо перетнути конус допоміжною січною площиною Ω, що проходить через пряму l, то утвориться коло з радіусом що дорівнює розміру:
248. Який спосіб доцільно вибрати для знаходження точок перетину прямої з похилим циліндром: a) [ ] заміни площин проекцій; b) [ ] центрального проекціювання; c) [ ] паралельного косокутнього проекціювання; d) [ ] плоскопаралельного перенесення. Точками перетину прямої l із пірамідою будуть
Точками перетину прямої l з циліндром будуть
Точками перетину прямої l із сферою будуть
|