Свойства первообразной.
Свойства первообразной. Перечислим свойства первообразной. 1. Если F– первообразная для функции f, то F + С, где С – константа, также является первообразной для той же функции. Действительно, (F + С)' = F' + С ' = f + 0 = f. 2. Если F1 и F2 – две первообразные для одной и той же функции f, то они отличаются на постоянное слагаемое. 3. Действительно, пусть F и G – первообразные для функций f и g соответственно. Тогда F + G является первообразной для функции f + g: (F + G)' = F' + G' =f + g. 4.
Дадим строгое математическое определение понятия неопределенного интеграла. Выражение вида Определение. Неопределенным интегралом Напомним, что
Задача нахождения неопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю. Например, известно, что Задача нахождение неопределенного интеграла от функций не столь простая и легкая, как кажется на первый взгляд. Во многих случаях должен быть навык работы с неопределенными интегралами, должен быть опыт, который приходит с практикой и с постоянным решением примеров на неопределенные интегралы. Стоит учитывать тот факт, что неопределенные интегралы от некоторых функций (их достаточно много) не берутся в элементарных функциях.
|

 является «неопределенным» в том смысле, что он обозначает какую-нибудь первообразную.
является «неопределенным» в том смысле, что он обозначает какую-нибудь первообразную.

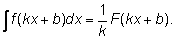 Действительно, вычислим производную от F(kx + b): (F(kx + b))' = kF '(kx + b) = kf (kx + b). Отсюда F (kx + b) является первообразной для функции kf (kx + b).
Действительно, вычислим производную от F(kx + b): (F(kx + b))' = kF '(kx + b) = kf (kx + b). Отсюда F (kx + b) является первообразной для функции kf (kx + b).
 называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом
называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом  всегда присутствует dx.
всегда присутствует dx.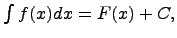 или
или  Функцию
Функцию  называют первообразной функции
называют первообразной функции  . Первообразная функции
. Первообразная функции  - дифференциал функции
- дифференциал функции 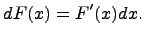
 , тогда получается, что
, тогда получается, что  , здесь
, здесь  - произвольная постоянная.
- произвольная постоянная.


