Цель настоящего пособия – обеспечение единства учебного процесса при изучении
Перечислим свойства первообразной. 1. Если F– первообразная для функции f, то F + С, где С – константа, также является первообразной для той же функции. Действительно, (F + С)' = F' + С ' = f + 0 = f. 2. Если F1 и F2 – две первообразные для одной и той же функции f, то они отличаются на постоянное слагаемое. 3. Действительно, пусть F и G – первообразные для функций f и g соответственно. Тогда F + G является первообразной для функции f + g: (F + G)' = F' + G' =f + g. 4.
40. Определение неопределенного интеграла. Дадим строгое математическое определение понятия неопределенного интеграла. Выражение вида Определение. Неопределенным интегралом Напомним, что
Задача нахождения неопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю. Например, известно, что Задача нахождение неопределенного интеграла от функций не столь простая и легкая, как кажется на первый взгляд. Во многих случаях должен быть навык работы с неопределенными интегралами, должен быть опыт, который приходит с практикой и с постоянным решением примеров на неопределенные интегралы. Стоит учитывать тот факт, что неопределенные интегралы от некоторых функций (их достаточно много) не берутся в элементарных функциях.
ОГЛАВЛЕНИЕ 1..: Введение в биофизику. Моделирование процессов________________________________________ 7 2..: Пространственная организация биополимеров. Классификация структур биополимеров 9 3..: Пространственная структура белков и определяющие ее силы_______________ 11 4..: Пространственная организация белков. Сворачиваемость белков_____________ 13 5..: Ферментативный катализ. Взаимодействие биомакромолекул с лигандами. Фермент-субстратные взаимодействия_____________________________________________ 14 6..: Ферментативный катализ. Аллостерические эффекты. Кооперативность____ 16 7. Итоговое занятие: Структура и свойства биомакромолекул__________________________ 18 8..: Спектральные методы исследования макромолекул. Абсорбционная спектрофотометрия________________________________________________________________________ 20 9..: Спектральные методы исследования макромолекул. Флуоресцентные методы_ 21 10..: Перенос электрона и миграция энергии в биосис.х___________________________________ 23 11..: Метод электронного парамагнитного резонанса в исследованиях свойств биосистем__ 24 12..: Метод ядерного магнитного резонанса в исследованиях свойств биосистем___________ 26 13..: Заключительно практическое занятие: Физические методы исследования биомакромолекул________________________________________________________________________ 29 14..: Динамические модели биологических процессов______________________________ 34 15..: Процессы самоорганизации в распределенных биологических сис.х.______________________ 36 16..: Термодинамика биологических процессов.___________________________________ 37 17. Итоговое занятие: биофизика сложных систем._____________________________________ 39
ПРЕДИСЛОВИЕ Цель настоящего пособия – обеспечение единства учебного процесса при изучении Пособие составлено в соответствии с государственным стандартом, утвержденным примерным планом дисциплины и рабочей программой по биофизике, утвержденной в 2005 г. Целью преподавания Общей и медицинской биофизики на медико-биологическом факультете является подготовка специалистов, владеющих теоретическими и практическими знаниями основных разделов биофизики в соответствии с их квалификационной характеристикой, и дающих возможность выпускнику медико-биологического факультета по специальности 60112 – Медицинская биохимия вести самостоятельную научную работу в области биохимии Биофизика изучается студентами третьего и четвертого курсов медико–биологического факультета (V – VII семестры) после получения исходных базовых знаний по химии, математике, физике, биологии, морфологии, физиологии, а также философии. Биофизика является интегративной фундаментальной наукой в системе медико – биологического образования, изучающая физические свойства биологических объектов, лежащие в основе функционирования живых организмов, с использованием методов теоретической и экспериментальной физики, трансформированными с учетом особенностей биологических объектов. Биофизика – центральная профилирующая дисциплина, синтезирующая совокупность ранее полученных знаний, которая вместе с другими дисциплинами медико – биологического (общая патология, микробиология, вирусология, иммунология, биохимия, фармакология, медицинская генетика), клинического (хирургия, терапия, неврология, педиатрия) и прикладного профиля (вычислительная техника, медицинская электроника) открывает возможность для самостоятельной работы в области исследования природы и механизмов развития патологических процессов, для совершенствования существующих и разработки новых методов диагностики, а также современных медицинских технологий.
|

 является «неопределенным» в том смысле, что он обозначает какую-нибудь первообразную.
является «неопределенным» в том смысле, что он обозначает какую-нибудь первообразную.

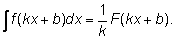 Действительно, вычислим производную от F(kx + b): (F(kx + b))' = kF '(kx + b) = kf (kx + b). Отсюда F (kx + b) является первообразной для функции kf (kx + b).
Действительно, вычислим производную от F(kx + b): (F(kx + b))' = kF '(kx + b) = kf (kx + b). Отсюда F (kx + b) является первообразной для функции kf (kx + b).
 называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом
называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом  всегда присутствует dx.
всегда присутствует dx.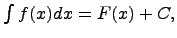 или
или  Функцию
Функцию  называют первообразной функции
называют первообразной функции  . Первообразная функции
. Первообразная функции  - дифференциал функции
- дифференциал функции 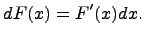
 , тогда получается, что
, тогда получается, что  , здесь
, здесь  - произвольная постоянная.
- произвольная постоянная.


