IV. Узагальнення і систематизація знань
Виконання усних вправ: 1. Який метод потрібно використати для розв’язання даного рівняння: а) б) в) Виконання письмових вправ: 1. Розв’язати рівняння Розв’язання 1-й спосіб:
У процесі розв’язування ми врахували той факт, що якщо 2-й спосіб:
Відповідь:
2. Розв’язати рівняння Розв’язання Скористаємося формулою
Відповідь:
3. Розв’язати рівняння Розв’язання Наведемо дві форми запису розв’язання вихідного рівняння. І форма запису розв’язання. ОДЗ: Знаходимо значення х, що задовольняють рівняння Оскільки через ОДЗ Відповідь:
ІІ форма запису розв’язання.
Відповідь:
4. Визначити кількість цілих значень параметра а, при яких рівняння Розв’язання
Відповідь: 9.
5. Розв’язати рівняння
Розв’язання Згрупуємо доданки в лівій і правій частинах рівняння:
Відповідь:
6. Розв’язати рівняння Розв’язання
Кожний множник отриманого рівняння прирівнюємо до нуля і знаходимо його корені: Відповідь:
7. Розв’язати рівняння Розв’язання Поділимо обидві частини рівняння на
Перевіримо, чи Відповідь:
8. Розв’язати рівняння Розв’язання Зробимо підстановку Тоді Значить Перевіримо, чи не є розв’язком даного рівняння Відповідь:
9. Розв’язати рівняння Розв’язання Позначивши
або Найпростішим методом розв’язування рівняння (1) є метод введення допоміжного кута:
Друге рівняння сукупності (2) розв’язків не має, оскільки Відповідь:
10. Розв’язати рівняння Розв’язання Скористаємось формулами зведення для правої частини рівняння.
Для Відповідь: 2.
11. Розв’язати рівняння Розв’язання
Відповідь: 12. Розв’яжіть систему рівнянь Розв’язання Згідно з властивостями тригонометричних функцій, що Тоді добуток Відповідь:
13. Знайдіть усі дійсні значення параметра а, при яких рівняння Розв’язання Замінимо
Отже, рівняння набуває вигляду
Зробимо оцінку Отже,
Відповідь: для для
14. Розв’язати рівняння Розв’язання Можна замінити (а): (б):
Перевіримо, чи не є розв’язком даного рівняння Відповідь:
15. Решите систему уравнений:
Решение. Сложив уравнения системы (9), а затем вычтя из второго уравнений первое, получим систему, равносильную системе (9):
откуда последовательно находим x + y = Пn, y - x = П/2 + 2Пk x = П (n/2 + k + 1/4) y = П (n/2 + k + 1/4) Ответ: (П (n/2 + k + 1/4); П (n/2 + k + 1/4))
16. Решить систему уравнений:
17. Решить систему уравнений:
Р е ш е н и е. Складывая и вычитая эти два уравнения, получим:
Рассмотрим отдельно каждую из ветвей второго уравнения:
|

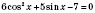 (зведення до квадратного рівняння)
(зведення до квадратного рівняння) (розкладання на множники)
(розкладання на множники) (метод введення допоміжного кута)
(метод введення допоміжного кута) .
.







 ,
,  , то
, то  можна покласти таким, що дорівнює
можна покласти таким, що дорівнює  .
.



 .
.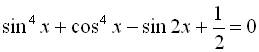 .
. , тоді
, тоді 

 . Зробимо заміну
. Зробимо заміну  :
:

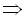
 Повернемось до заміни:
Повернемось до заміни:

 .
. .
.

 і
і  ; якщо
; якщо 
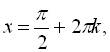
 ; якщо
; якщо 

 .
. .
.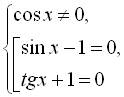

 має розв’язки.
має розв’язки. . За властивістю функції
. За властивістю функції  –
–  , тому
, тому 

 . Цілими значеннями, які належать отриманому проміжку, є: –5; –4; –3; –2; –1; 0; 1; 2; 3. Їх кількість – 9.
. Цілими значеннями, які належать отриманому проміжку, є: –5; –4; –3; –2; –1; 0; 1; 2; 3. Їх кількість – 9. .
. . За формулою перетворення суми синусів, а також за формулою косинуса подвійного кута, отримаємо
. За формулою перетворення суми синусів, а також за формулою косинуса подвійного кута, отримаємо 



 . Звідси
. Звідси 




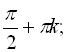


 .
. .
.




 .
.












 .
.

 :
:





 . Отже
. Отже 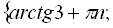

 .
. .
. ,
, 
 .
.


 .
.



 .
. .
. .
.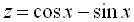 , дістанемо
, дістанемо 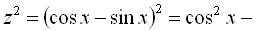

 . Тоді початкове рівняння запишеться у вигляді
. Тоді початкове рівняння запишеться у вигляді 
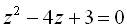
 Повернемось до заміни:
Повернемось до заміни: (1)
(1)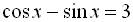 . (2)
. (2)



 , а число
, а число  .
. .
. . У відповіді зазначте кількість розв’язків на проміжку
. У відповіді зазначте кількість розв’язків на проміжку 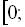
 .
.





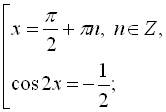



 ;
;  . Отже розв’язків на відрізку
. Отже розв’язків на відрізку  .
. Перші дві тригонометричні нерівності нашої комбінованої системи розв’язуємо з урахуванням властивостей тригонометричних функцій. Тоді маємо:
Перші дві тригонометричні нерівності нашої комбінованої системи розв’язуємо з урахуванням властивостей тригонометричних функцій. Тоді маємо: 




 .
. У відповідь запишіть добуток
У відповідь запишіть добуток  , якщо
, якщо 
 – розв’язок системи рівнянь.
– розв’язок системи рівнянь. та
та  , отримаємо:
, отримаємо:  звідки
звідки  Дана система нерівностей виконується лише при
Дана система нерівностей виконується лише при  ;
;  .
. .
. .
.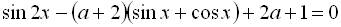 має розв’язок.
має розв’язок. через
через  , тоді
, тоді 

 , звідси
, звідси  .
.
 . Розв’яжемо квадратне рівняння відносно змінної
. Розв’яжемо квадратне рівняння відносно змінної  ;
; 


 на
на  :
:  ; за допомогою введення допоміжного кута
; за допомогою введення допоміжного кута 
 (І). Оскільки
(І). Оскільки 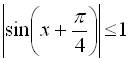 , то й
, то й  , тобто
, тобто 
 , або
, або  .
. не задовольняє наші умови, тому
не задовольняє наші умови, тому  , а оскільки
, а оскільки  , і з рівності (І)
, і з рівності (І) 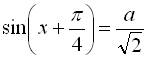

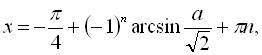
 розв’язків немає;
розв’язків немає;
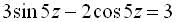 .
. через х, а потім зробити підстановку
через х, а потім зробити підстановку  . Тоді
. Тоді 

 або
або  . Повернувшись до підстановки
. Повернувшись до підстановки  (а) або
(а) або 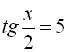 (б), розв’яжемо по черзі рівняння (а) і (б):
(б), розв’яжемо по черзі рівняння (а) і (б):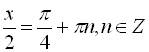

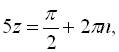

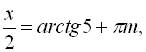
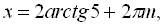


 .
.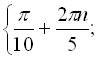
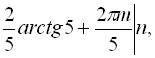
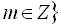 .
.






