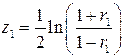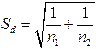Корреляционный анализ

 

Корреляция – статистическая взаимосвязь двух параметров между собой; сила этой вза­имосвязи измеряется т.н. коэффициентом корреляции.

Коэффициент корреляции (r) – показывает, в какой степени значения одного параметра изменяются при пропорциональном изменении значений другого параметра. Проще говоря, коэффициент корреляции показывает, на какую величину изменится значение одного параметра при изменении значения другого параметра на единицу. Т.о., если коэффициент корреляции равен +0,85, то при изменении значения любого из параметров на +1 значение другого параметра также вырастет на 0,85; если же коэффициент корреляции равен –0,47, то при изменении величины любого из параметров на +1 значение другого параметра изменится на –0,47, т.е. уменьшится на 0,47. Величина коэффициента корреляции изменяется от –1 до +1, причем 0 означает отсутствие корреляции.

Если значение коэффициента корреляции положительное (больше нуля), такая корреляция называется прямой или положительной. Если значение коэффициента корреляции отрицательное (меньше нуля), то соответствующая корреляция называется обратной или отрицательной. Прямая корреляция означает, что при увеличении одного параметра другой также увеличивается, в случае обратной корреляции – соответственно, уменьшается.

Как для остальных видов статистического анализа, для корреляции рассчитывается показатель вероятности нулевой гипотезы (р), который должен быть равен или меньше заранее оговоренного уровня значимости (α) – см. раздел 8 настоящей главы. Обычно уровень значимости устанавливается равным 0,05 (что обычно для биомедицинских исследований), с возможным внесением поправки на проблему множественных сравнений (см. выше).

В зависимости от величины по модулю коэффициента корреляции сила корреляционной взаимосвязи классифицируется как:

| r | ≤ 0,25 – слабая корреляция;

0,25 < | r | < 0,75 – умеренная корреляция (корреляция средней силы);

| r | ≥ 0,75 – сильная корреляция.

Возможны ситуации, когда найденная корреляционная зависимость не может быть корректно учтена и использована при формулировке выводов исследования:

1. Корреляция статистически значима (р меньше или равен принятому уровню значимости, например, 0,05), но коэффициент корреляции слишком мал (≤0,25). Такие корреляции могут представлять интерес для исследователей неявных тенденций в больших популяциях, но для клиники они, как правило, не важны, поскольку описываемые ими взаимообусловленные изменения параметров организма слишком незначительны. Проще говоря, такая корреляция статистически значима, но клинически незначима. Подобные зависимости во множестве выявляются при анализе выборок большого размера. Обычно в клинических исследованиях принимают во внимание как минимум корреляции средней силы;

2. Коэффициент корреляции высок, но она статистически незначима (р>0,05 либо иного уровня значимости, принятого исследователями). Проще говоря, такая корреляция клинически значима, но статистически незначима. Подобные ситуации, как правило, имеют место при малом размере анализируемой выборки; при этом увеличение размера выборки до рекомендованного (см. Главу III, раздел 6.5) может повысить статистическую значимость корреляции до приемлемой (в случае, если корреляционная зависимость действительно имеет место). Необходимо помнить о том, что в малых выборках высока вероятность выявления взаимосвязей, обусловленных исключительно случайным сочетанием значений параметров, причем чем меньше размер выборки, тем выше роль случайности в результатах статистической обработки. Как указывалось ранее, статистическая обработка данных, полученных при анализе выборок, включающих менее 20 наблюдений, почти всегда не имеет смысла.

Методы корреляционного анализа могут быть параметрическими (предназначенными для анализа взаимозависимости нормально распределенных данных) и непараметрическими.

 

Параметрический корреляционный анализ – Пирсона.

Критерии применимости корреляционного анализа Пирсона:

1. Все учитываемые признаки должны быть нормально распределены;

2. Все учитываемые признаки должны быть количественными.

 

Непараметрический корреляционный анализ – Спирмена, Тау Кендалла, Гамма.

Критерии применимости перечисленных разновидностей корреляционного анализа:

1. Учитываемые признаки – количественные, распределения которых не являются нормальными либо неизвестны (по крайней мере, для одного из признаков);

2. Возможен анализ смеси количественных и качественных (порядковых) признаков;

3. Возможен анализ нескольких качественных (порядковых) признаков.

Ранговая корреляция Спирмена (ρ) – универсальный метод, используется для оценки взаимосвязи количественных (независимо от вида распределения) и/или порядковых (качественных) признаков. Наиболее популярный метод корреляционного анализа.

Ранговая корреляция Тау Кендалла (τ) – используется для оценки взаимосвязи порядковых признаков или смеси количественных и порядковых признаков.

Гамма-корреляция (γ) – используется, когда в анализируемых переменных имеется много вариант, значения которых совпадают.

 

Как и для прочих статистических показателей, для коэффициента корреляции может быть рассчитан доверительный интервал. Вычисляется он следующим образом:

1. Вычисляется функция z:

 

Здесь r – коэффициент корреляции.

 

2. Вычисляется стандартная ошибка m для z:

 

Здесь n – количество наблюдений в переменных, для которых рассчитывается коэффициент корреляции.

 

3. Вычисляются нижний и верхний пределы функции z (z₁ и z₂):

 

Здесь t – значение t-критерия для данного числа степеней свободы (см. выше: df = n–1) и заданного уровня значимости α (обычно р≤0,05). Подсчет t-критерия обычно выполняется при помощи специальной функции программы статистической обработки. Например, в программах семейства Statistica этот подсчет реализован следующим образом (см. рис. 23):

 

Рис. 23. Подсчет t-критерия Стьюдента для данного числа степеней свободы и заданного уровня значимости α, реализованный в программах Statistica 7.0 и 8.0.

 

4. Вычисляются нижний и верхний пределы ДИ для коэффициента корреляции r:

 

С вероятностью 95% истинное значение коэффициента корреляции, вычисленное на основе анализа генеральной совокупности, находится в указанных границах.

 

Коэффициенты корреляции можно попарно сравнивать. Для проверки гипотезы о равенстве двух корреляций (H0) величины сравниваемых коэффициентов корреляций r₁ и r₂ подвергаются z-преобразованию Фишера:

 

 

 

После этого вычисляется стандартная ошибка разницы по формуле:

 

 

Здесь:

n₁ – количество пар значений переменных для первого коэффициента корреляции;

n₂ – количество пар значений переменных для второго коэффициента корреляции.

 

Затем вычисляется значение t-критерия Стьюдента по формуле: t = (z₁ – z₂)/S_d

Для дальнейших расчетов берется абсолютное значение этого числа.

 

Затем вычисляется количество степеней свободы (df). В данном случае df = (n₁ + n₂) – 2

 

Зная t и df, при помощи таблицы критических значений t-критерия Стьюдента можно определить р (см. рис. 24).

 

Рис. 24. Сокращенная таблица критических значений t-критерия Стьюдента. Здесь df – число степеней свободы, α – уровень значимости (в данном случае будет соответствовать р).

 

Можно также вычислить доверительные интервалы для обоих сравниваемых коэффициентов корреляции и посмотреть, не пересекаются ли они: если ДИ пересекаются (границы ДИ накладываются друг на друга), то коэффициенты корреляции значимо не различаются.

 

Вышеописанные вычисления можно быстро выполнить при помощи описанного ранее диалогового окна программы Statistica версий 7.0 и 8.0 (см. рис. 22). Для этого необходимо знать величины собственно сравниваемых коэффициентов корреляции, число наблюдений (n) для каждого из них, а также тип статистической гипотезы (направленная или ненаправленная, т.е. одно- или двусторонняя – см. выше).

 

Ведя речь о корреляционном анализе, необходимо указать, что нельзя слепо доверяться его результатам!!! Дело в том, что довольно простая формула, по которой рассчитывается коэффициент корреляции, ничего не знает о том, существует ли взаимосвязь между анализируемыми признаками в действительности – она лишь анализирует по ряду формальных критериев функции, описывающие изменение этих признаков, и сравнивает полученные результаты друг с другом. Проще говоря, если два признака по чистой случайности изменяются сходным образом, они будут коррелировать между собой. Естественно, выявленные при помощи таких корреляций «взаимосвязи» пополняют копилку научных анекдотов. Так, на рис. 25 представлена взаимосвязь между количеством убийств в США и частотой использования браузера Internet Expolrer с очевидной сильной прямой корреляцией между указанными факторами, причем данные удивительным образом даже не подтасованы [4, 3].

 

Рис. 25. Взаимосвязь между количеством убийств в США и доли браузера Internet Explorer на рынке браузеров (данные за 2006-2011 гг.).

 

Еще один замечательный пример абсурдной корреляции показан на рис. 26, где отчетливо прослеживается взаимосвязь между количеством скачиваний известной свободной операционной системы Linux и количеством поисковых запросов по поводу прыщей (данные из кэша поисковых запросов портала Yandex).

В целом, выявление при анализе взаимосвязи неких факторов А и В статистически значимого коэффициента корреляции, соответствующего взаимозависимости средней силы и более, может свидетельствовать о том, что в реальности:

1. Признак А влияет на признак В;

2. Признак В влияет на признак А;

3. На оба признака влияет неизвестный третий фактор С;

4. Признаки А и В не влияют друг на друга, но по чистой случайности изменяются сходным образом (параллельно).

 

Рис. 26. Взаимосвязь между количеством скачиваний операционной системы Linux и количеством поисковых запросов по поводу прыщей (данные из кэша Yandex).

 

Таким образом, корреляционный анализ устанавливает наличие и силу только статистической связи, и наличие корреляции двух признаков (любой силы) не может интерпретироваться как доказательство причинно-следственной связи этих признаков.

Говоря о практической стороне дела, при анализе коэффициентов корреляции необходимо принимать во внимание следующие соображения:

1. Корреляция, даже статистически высокозначимая, должна характеризоваться достаточным числом наблюдений в коррелирующих переменных (не менее 20 в каждой);

2. Лучше устанавливать уровень значимости (α) с поправкой на множественность сравнений, т.е. он должен быть разумно низким, например, ≤0,01 или даже ≤0,001 – это повышает вероятность того, что такая корреляция не будет являться результатом случайного совпадения значений анализируемых признаков;

3. Каждая выявленная корреляционная зависимость должна получать четкое логическое обоснование, подтверждая некоторый известный науке феномен либо внятную, обоснованную гипотезу экспериментаторов.

 

Существует универсальная мера качества (объясняющей способности) причинных статистических моделей, применяющаяся, главным образом, в дисперсионном и регрессионном анализах (см. далее), но также и при вычислении коэффициентов корреляции. Это т.н. доля объясненной дисперсии, которая рассчитывается по формуле: r²×100 (%). Более точно – это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели) в общей дисперсии зависимой переменной. Чем больше величина доли объясненной дисперсии, тем выше качество объясняющей модели.