Представление и описание распределений количественных данных
Любое вероятностное распределение может быть охарактеризовано при помощи показателей центральной тенденции и разброса (дисперсии) данных. К показателям центральной тенденции относятся: среднее арифметическое, медиана, мода и (в особых случаях) среднее геометрическое. Мода – показатель, реже всего применяемый для описания распределения. По сути своей мода – это варианта, которая наиболее часто встречается в вариационном ряду. Проще всего вычислить моду, построив таблицу частотного распределения, в которую вносят частоту встречаемости каждой из вариант (см. выше). Например, мода набора данных (0, 0, 1, 1, 1, 1, 2, 2, 2, 3, 4, 6) равна 1, так как эта варианта встречается 4 раза – чаще любой другой. Если окажется, что все значения в вариационном ряду встречаются с одинаковой частотой (например, однократно), то у такого распределения не будет моды. Подобное распределение называется равномерным (см. рис. 13).
Рис. 13. Равномерное распределение – распределение, не имеющее выраженной моды.
Если какая-либо одна варианта в вариационном ряду встречается чаще других, такое распределение называется унимодальным (см. рис. 14).
Рис. 14. Унимодальное распределение, имеющее вид нормального (симметричный, колоколообразный). Мода в данном случае соответствует 30.
Унимодальный вид типичен для распределений практически любых признаков в биомедицинских исследованиях (при условии однородности исследуемой выборки и ее достаточной репрезентативности – см. Главу III), поскольку соответствует фундаментальному биологическому принципу, согласно которому, среднее значение любого признака преобладает, а остальные его значения встречаются тем реже, чем больше отклоняются от среднего. Впрочем, ассиметричные распределения тоже являются унимодальными (см. рис. 7, 8).
Если окажется, что две и более варианты встречаются в распределении чаще других, у распределения будут две и более моды. Подобное распределение называется полимодальным (бимодальным, тримодальным и т.п.) – см. рис. 15. Полимодальное распределение обычно является признаком выраженной неоднородности изучаемой выборки, о чем свидетельствует наличие двух и более пиковых значений изучаемого признака.
Рис. 15. Полимодальное (в данном случае – бимодальное) распределение.
Медиана – среднее значение набора данных, упорядоченных по возрастанию (т.е. вариационного ряда). Проще говоря, медиана – это значение, делящее набор данных на две половины, одна из которых состоит из вариант, величина которых меньше величины медианы, а другая – из вариант, величина которых больше величины медианы. Медиана – часто применяемая характеристика центральной тенденции вариационного ряда. Будучи центральным значением в вариационном ряду, медиана является также вторым квартилем или 50-м процентилем (50‰). Вместе с медианой часто определяют первый квартиль (Q1, 25-й процентиль, 25‰) и третий квартиль (Q3, 75-й процентиль, 75‰). Первый квартиль – значение в вариационном ряду, делящее набор данных на 2 части, в одной из которых – 25% значений, меньших, чем первый квартиль, а в другой – 75% значений, больших, чем первый квартиль. Соответственно, третий квартиль – это значение в вариационном ряду, делящее набор данных на 2 части, в одной из которых – 75% значений, меньших, чем третий квартиль, а в другой – 25% значений, больших, чем третий квартиль. Численное выражение расстояния между 1-м и 3-м квартилями называется «межквартильный размах». Порядковый номер варианты, являющейся медианой вариационного ряда с общим числом вариант n, вычисляется по формуле (n+1)/2. Если n нечетное, то полученному порядковому номеру соответствует одна из вариант, которая и будет являться медианой. Если n четное, то вычисленный порядковый номер попадет между двумя вариантами, и медиана будет равна среднему арифметическому обоих вариант. Позиция первого квартиля (Q1) вычисляется по формуле 0,25×(n+1), третьего квартиля (Q3) – по формуле 0,75×(n+1). При определении медианы в интервальных вариационных рядах сначала определяется интервал, в котором она находится (медианный интервал). Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Расчет медианы интервального вариационного ряда производится по формуле:
Ме = ХМе + iМе × (1/2∑f – SМе-1)/fМе, где
Ме – медиана интервального вариационного ряда; ХМе – начальное значение медианного интервала; iМе – величина медианного интервала; ∑f – сумма частот вариационного ряда (численность ряда); SМе-1 – сумма накопленных частот в интервалах, предшествующих медианному; fМе – частота медианного интервала.
Аналогично, первый и третий квартили интервальных вариационных рядов рассчитываются по следующим формулам:
Q1 = XQ1 +iQ1 × (1/4∑f – SQ1-1)/fQ1
Q3 = XQ3 + iQ3 × (3/4∑f – SQ3-1)/fQ3
В отличие от средней арифметической, медиана не так сильно подвержена воздействию крайних значений распределения. Обратите внимание, что следующие наборы данных различаются только одним (последним) наблюдением:
Набор А – 24, 25, 29, 29, 30, 31: среднее = 28,0, медиана = 29
Набор В – 24, 25, 29, 29, 30, 131: среднее = 44,7, медиана = 29
Различие в одном наблюдении значительно изменяет величину средней арифметической, но совершенно не меняет значение медианы. Таким образом, использование медианы более предпочтительно, если вариационный ряд смещен в одну или в другую сторону, или если набор данных имеет несколько очень больших или очень маленьких значений.
Среднее арифметическое – сумма величин всех вариант в вариационном ряду, разделенная на общее количество вариант (численность ряда). Вычисляется по формуле:
М – среднее арифметическое; Хi – варианта с положением i в вариационном ряду; n – общее количество вариант (численность вариационного ряда).
Пример: Во время вспышки гепатита А заболело 6 человек, клинические симптомы у которых появились в промежутке между 24 и 31 днями после заражения. Продолжительность инкубационного периода у заболевших лиц составила 29, 31, 24, 29, 30 и 25 дней. Соответственно, среднее арифметическое продолжительности инкубационного периода вычисляется в данном случае как (29 + 31 + 24 + 29 + 30 + 25)/6 = 28 суток. Среднее арифметическое используется чаще других видов характеристик центральной тенденции, т.к. оно обладает удобными статистическими свойствами. Например, сумма отклонений отдельных значений от среднего арифметического равна нулю. Поясним это на ранее рассмотренном примере вспышки гепатита А. Ниже в таблице 2 приведены данные, полученные вычитанием среднего инкубационного периода из отдельных инкубационных периодов, также приведена сумма полученных разностей – она равна нулю. Это означает, что среднее арифметическое является арифметическим центром распределения.
Таблица 2. Сумма отклонений отдельных значений вариационного ряда от его среднего арифметического равна нулю.
Среднее арифметическое иногда называют «центром тяжести» распределения. Это значит, что распределение будет находиться в равновесии, если поместить точку опоры в среднее значение, как показано на рис. 16.
Рис. 16. Среднее арифметическое – «центр тяжести» распределения.
Величина среднего арифметического находится в «центре тяжести» распределения, но в действительности плохо отражает центральную тенденцию. При наличии в вариационном ряду одного очень большого (выступающего, экстремального) значения средняя арифметическая может стать больше, чем все остальные варианты в распределении, за исключением выступающего (например, в наборе данных 24, 25, 29, 29, 30, 131 среднее = 44,7). Из-за того, что среднее арифметическое настолько чувствительно к воздействию экстремальных значений, оно неприменимо для описания асимметрично распределенных данных (смещенных распределений); для этого лучше подходит медиана (см. выше).
Среднее геометрическое – аналог среднего арифметического для дискретных распределений, которые описываются формулами экспоненциальной (1, 2, 4, 8, 16 и т.д.) или логарифмической (1/2, 1/4, 1/8, 1/16 и т.д.) функций. Примером из повседневной медицинской практики являются массивы данных, состоящие из замеров титров специфических антител в сыворотке крови. Среднее геометрическое вычисляется извлечением корня степени n из произведения всех значений – вариант признака Х:
х1…хn – все значения вариант в вариационном ряду; n – общее количество вариант (численность вариационного ряда).
На практике среднее геометрическое подсчитывается по формуле:
Покажем на примере, как подсчитать среднюю геометрическую следующего набора данных: 10, 10, 100, 100, 100, 100, 10000, 100000, 100000, 1000000. Так как все значения в ряду представляют собой степени 10, имеет смысл использовать 10 в качестве основания логарифмов. Прологарифмируем каждое значение вариационного ряда по основанию 10:
log10(xi) = 1, 1, 2, 2, 2, 2, 4, 5, 5, 6
Подсчитаем среднее значений логарифмов, сложив их и разделив на число наблюдений (в данном случае 10):
Среднее log10(xi) = (l + l + 2 + 2 + 2 + 2 + 4 + 5 + 5 + 6)/10 =30/10 =3
Возведя основание логарифма (10) в степень среднего значения логарифмов, вычисленного на предыдущем этапе (3), получаем значение среднего геометрического: 103 = 1000.
К показателям разброса (дисперсии) данных относятся: размах, минимальное значение, максимальное значение, процентили, квартили, межквартильный размах, дисперсия, среднеквадратическое отклонение, стандартная ошибка среднего, доверительный интервал. Размахом набора данных называется разница между наибольшим (максимальным) и наименьшим (минимальным) значениями вариационного ряда. В математической статистике размах обычно выражают одним числом – разностью максимального и минимального значений. В эпидемиологии величину размаха принято показывать двумя цифрами – минимальным и максимальным значениями вариант. N-й процентиль распределения – значение варианты, которому равно или меньше его N процентов вариант в данном ряду данных. Медиана делит вариационный ряд строго пополам, вследствие чего является 50-м процентилем (иногда говорят также «2-й квартиль» или Q2). Помимо медианы, часто используются 25-й и 75-й процентили (соответственно, Q1 и Q3, см. выше). Межквартильный размах подсчитывается как разность между первым и третьим квартилями. В этом диапазоне лежит примерно половина набора нормально распределенных данных, вне его с каждой стороны находится примерно по четверти наблюдений. Ранее было показано, что если вычесть среднее арифметическое из значения каждой варианты, сумма полученных разностей будет равна 0. Эта идея вычитания средней из каждого наблюдения лежит в основе расчета двух показателей разброса данных – дисперсии (называемой также вариансой) и среднеквадратического отклонения. Для получения этих показателей все разности между вариантами и средним арифметическим возводятся в квадрат с целью устранения отрицательных чисел. Затем квадраты разностей складываются и делятся на n-1 для нахождения «среднего» квадрата разности. Такая «средняя» величина называется дисперсией и обозначается латинской буквой «сигма» в квадрате (σ2, или s2). Чтобы вернуться к первоначальной размерности, из σ2 (значения дисперсии) извлекается квадратный корень. Квадратный корень из дисперсии называется среднеквадратическим отклонением (σ, s, СКО). Формулы для расчета дисперсии и СКО приведены ниже.
σ2 – дисперсия; x i – значение варианты с номером i в вариационном ряду, причем значение i варьирует от 1 до n;
Соответственно,
Для иллюстрации данных формул вернемся к примеру, где сумма отклонений отдельных вариант от среднего арифметического вариационного ряда равна нулю (см. таблицу 2):
Дисперсия (s2) = (сумма квадратов разностей)/(n–1) = 40/5 = 8
Среднеквадратическое отклонение (s) =
Как указывалось ранее в предыдущем разделе, при условии нормального вероятностного распределения вариационного ряда в пределах М ± 1σ всегда должно находиться приблизительно 68,3% вариант, в пределах М ± 2σ – 95,4% вариант, и в пределах М ± 3σ – 99,7% вариант. Таким образом, любое нормальное распределение может быть однозначно охарактеризовано простым указанием среднего арифметического и соответствующего ему среднеквадратического отклонения (обычно в формате «М ± σ»). Несколько особняком стоят понятия «стандартная ошибка среднего арифметического» и «доверительный интервал». Как известно, общая совокупность лиц, имеющих интересующий исследователей признак либо подверженных интересующему исследователей воздействию, называется генеральной совокупностью (подробное определение с примерами см. в следующей главе). Как правило, исследователи не могут работать непосредственно с генеральной совокупностью ввиду ее большого размера и, соответственно, непомерной сложности и дороговизны подобных исследований. Ввиду этого, повсеместно практикуется работа с т.н. выборками, т.е. случайным образом отобранными из генеральной совокупности группами лиц. Для того, чтобы результаты исследования, проведенного с использованием выборки, в максимальной степени соответствовали аналогичным результатам, полученным на генеральной совокупности, выборка должна быть репрезентативной, т.е. должна в максимальной степени соответствовать генеральной совокупности по всем характеристикам (половой, возрастной состав, вредные привычки, фоновые заболевания, характер питания, годовой доход, место проживания участников и т.д.), важным для результата проводимого эксперимента. Обычно репрезентативность достигается применением рандомизации в процессе формирования исследуемых групп, т.е. собственно выборки (см. следующую главу). Таким образом, при статистической обработке результатов, полученных при исследовании выборки, замещающей генеральную совокупность, предполагается, что она: – сформирована случайным образом, без вмешательства каких бы то ни было прогнозируемых систематических факторов отбора; – репрезентативна, т.е. максимально соответствует генеральной совокупности по всем основным параметрам, влияющим на результаты эксперимента. Тем не менее, в соответствии с базовыми принципами теории вероятностей, выборка не может абсолютно соответствовать по своим характеристикам генеральной совокупности, и степень этого соответствия тем меньше, чем меньше размер выборки по сравнению с таковым генеральной совокупности. В этой связи показатели центральной тенденции, рассчитанные по данным выборки, должны быть экстраполированы на генеральную совокупность с указанием точности экстраполяции. Стандартная ошибка среднего и доверительный интервал как раз и являются показателями точности экстраполяции. Стандартная ошибка среднего (m) – это теоретическое среднеквадратическое отклонение всех средних арифметических, полученных из всех выборок размера n, извлекаемых из генеральной совокупности, зависящее от совокупной дисперсии (сигма) и размера выборки (n). Проще говоря, стандартная ошибка среднего – это усредненная разница по модулю («среднеквадратическое отклонение») между средним арифметическим генеральной совокупности и всеми средними арифметическими, которые могут быть рассчитаны при работе со всеми выборками размера n, которые теоретически можно сформировать из данной генеральной совокупности. Стандартная ошибка среднего рассчитывается следующим образом:
Здесь: m – стандартная ошибка среднего; σ – среднеквадратическое отклонение для данного вариационного ряда; n – численность (размер) выборки.
Широко распространен ошибочный подход, при котором для описания дисперсии непрерывных количественных данных используют стандартную ошибку среднего вместо среднеквадратического отклонения, пытаясь продемонстрировать малую вариабельность своих данных, так как по определению величина m всегда меньше σ (в квадратный корень из n раз). Другим частым поводом для использования m вместо σ является то, что исследователи сталкиваются с ситуацией, когда σ превышает величину среднего арифметического (М), и, соответственно, запись «M±σ» в большинстве случаев (когда переменная может принимает только положительные значения) оказывается бессмысленной. Не зная, как описывать распределения, отличные от нормального, авторы указывают «M±m», так как m всегда меньше σ, и это позволяет избежать заведомо некорректной ситуации. В подобных случаях точность оценки среднего рекомендуется приводить в виде 95% доверительного интервала (ДИ). В случае нормального распределения границами такого ДИ являются M±1,96m (см. далее). Смысл понятия «доверительный интервал» близок к таковому стандартной ошибки среднего, но есть и различия: если стандартная ошибка может быть вычислена только для среднего арифметического, то доверительный интервал можно рассчитать для любого статистического показателя, включая среднее арифметическое, медиану и квартили, а также доли, частоты и отношения, включая отношения рисков и шансов, о которых пойдет речь далее. Х%-й доверительный интервал – это интервал значений, в который с вероятностью Х (%) попадает соответствующая характеристика генеральной совокупности. Естественно, предполагается, что данная характеристика была определена при исследовании рэндомной (сформированной случайным образом), репрезентативной выборки. Обычно при проведении биомедицинских исследований Х принимают равным 95%, что считается достаточным, и тогда выражение выглядит как «95% доверительный интервал (95% ДИ)». Тем не менее, никто не мешает взять другое значение Х; иногда так и делается – в этом случае обычно используют 99%. Программы для статистической обработки данных позволяют подсчитать доверительный интервал для среднего арифметического с любым заданным Х; возможность же определить доверительный интервал для других статистических показателей, таких, как медиана или отношения шансов/рисков, встречается гораздо реже. Доверительный интервал имеет нижний и верхний пределы (соответственно, минимальное и максимальное значения интервала, которые и приводятся в качестве характеристик точности оценки статистического параметра). 95% ДИ для среднего арифметического нормально распределенного вариационного ряда рассчитывается по следующим формулам:
Нижний 95% доверительный предел = М – (1,96×m)
Верхний 95% доверительный предел = М + (1,96×m), где
М – среднее арифметическое ряда данных; 1,96 – коэффициент для вычисления 95% вероятности (для других значений Х% он будет другим, например, для 99% данный коэффициент равен 2,58, а для 99,9% – 3,28); m – стандартная ошибка среднего (см. выше).
Формулы подсчета 95% ДИ для медианы и квартилей следующие:
Здесь: j – нижний предел доверительного интервала; k – верхний предел доверительного интервала; 1,96 – коэффициент для вычисления 95% вероятности (соответственно, 2,58 для 99% вероятности, 3,28 – для 99,9%); n – общее число наблюдений в выборке (численность вариационного ряда); q – квартиль (Q1 – 0,25, Q2 (Me) – 0,5, Q3 – 0,75).
Формат представления рассчитанного доверительного интервала следующий: М (95% ДИ: j…q) или Me (95% ДИ: j…q), например: М = 96,6 (95% ДИ: 90,2…101,4). Вместо троеточия можно использовать дефис, как в (95% ДИ: 90,2–101,4) – данный формат еще не устоялся, у него нет стандарта de facto. Тем не менее, в западной научной литературе указание доверительного интервала вместо стандартного отклонения – общепринятая практика; там ДИ обозначают как CI, т.е. «Confidence Interval». Рис. 17 иллюстрирует расположение пределов 95% доверительного интервала относительно среднего арифметического вариационного ряда.
Рис. 17. Среднее арифметическое вариационного ряда и расположение нижнего и верхнего пределов его 95% доверительного интервала на графике полигона частот.
Важное замечание: Обычно в результате вычислений различных статистических показателей возникает большее число значащих цифр, чем это было в исходных данных. Здесь необходимо помнить, что результаты расчетов не могут быть точнее, чем первичные данные измерений. Соответственно, в этом случае числовые данные необходимо округлять до десятичного знака, соответствующего таковому в исходных данных. Так, например, если артериальное давление измерялось с точностью до единиц мм рт. ст., то распределение должно описываться следующим образом: М = 145 ± 27 мм рт. ст. Кроме того, следует учитывать, что читатель обычно хорошо воспринимает числа, содержащие не более трех значащих цифр. Если приводятся дробные числа, не рекомендуется указывать более трех знаков после запятой (лучше – меньше). Помните, что никакая статистическая обработка не улучшит результаты плохо спланированного и неподобающим образом выполненного исследования. Это хорошо иллюстрирует поговорка «garbage in – garbage out», т.е. «мусор на входе – мусор на выходе!»
Заключение: Среднее арифметическое вариационного ряда – простой для понимания и удобный для использования статистический показатель, характеризующий центральную тенденцию вероятностных распределений данных. Тем не менее, в этом качестве у него есть ряд недостатков, ограничивающих его применение: 1. Среднее арифметическое может быть рассчитано только для непрерывных вариационных рядов. В случае дискретных либо интервальных вариационных рядов среднее арифметическое не имеет смысла, как не имеет смысла «средний пол» либо 2,66 землекопа; 2. Среднее арифметическое хорошо характеризует центральную тенденцию в симметрично (например, нормально) распределенных рядах данных. В случае ассиметричных (смещенных) распределений значение среднего арифметического смещается в сторону бóльших значений ряда, что хорошо иллюстрирует рис. 18.
Рис. 18. Смещение среднего арифметического относительно других показателей центральной тенденции вариационного ряда в ассиметричных распределениях. Данное распределение смещено вправо; Мо – мода, Ме – медиана, М – среднее арифметическое.
Таким образом: 1. Распределения, являющиеся приближенно нормальными (и только они), должны описываться средним арифметическим и среднеквадратическим отклонением (M±σ); 2. Для описания распределений, не являющихся нормальными (а это большинство распределений медико-биологических параметров), рекомендуется применять медиану и межквартильный размах. Межквартильный размах указывается в виде 25% и 75% процентилей (допускается и указание других процентилей, симметричных относительно медианы, например 10% и 90%). Пример: Ме (25%; 75%) = 60 (23; 78). 3. Во всех случаях, при любом виде распределений анализируемых данных допустимо использование 95% доверительного интервала как характеристики разброса значений в вариационном ряду. Если распределение симметричное, то его описание будет иметь вид «М (95% ДИ: нижний предел…верхний предел), если ассиметричное – то «Ме (95% ДИ: нижний предел…верхний предел). Вышеприведенные рекомендации кратко резюмированы в таблице 3.
Таблица 3. Способы описания центральной тенденции и разброса (дисперсии) данных в различным образом распределенных вариационных рядах.
Важно! Общее требование к представлению результатов исследований – указание количества наблюдений (n) для каждой исследуемой переменной.
При необходимости графического представления вышеперечисленных характеристик распределений количественных данных наиболее удобно пользоваться т.н. диаграммами вида «ящик-с-усами» («box-and-whisker plot»), или, проще, ящичными диаграммами. Подобные диаграммы действительно напоминают ящики с усами, установленные вертикально, и могут быть построены при помощи любой из обсуждавшихся выше программ для статистической обработки научных данных (рис. 19).
Рис. 19. Ящичные диаграммы – удобное и наглядное графическое отображение характеристик распределений количественных данных.
Обычно центр «ящика» – это, по выбору исследователя, либо среднее арифметическое, либо медиана вариационного ряда. Нижняя кромка «ящика» – чаще Q1, реже – (М–σ). Верхняя кромка «ящика» – обычно Q3, реже – (М+σ). Нижняя и верхняя засечки «усов» – обычно минимальное и максимальное значения вариант в ряду данных, соответственно. Тем не менее, по выбору исследователя (либо программы) это могут быть 10-й и 90-й (или другие) процентили, а точки выше и ниже их будут показаны как т.н. «выбросы» – случайные артефакты измерений. Ящичные диаграммы позволяют полностью представить себе все свойства анализируемых вероятностных распределений, ввиду чего их используют чаще, чем построение полигона частот либо гистограммы частот (см. выше).
|




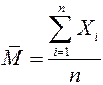 , где
, где
 , где
, где
 , где
, где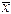 – среднее арифметическое вариационного ряда.
– среднее арифметическое вариационного ряда.
 =
=  ≈ 2,83
≈ 2,83







