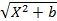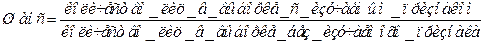Регрессионный анализ
Регрессионный анализ – статистический метод исследования влияния одной или нескольких «независимых» переменных на «зависимую» переменную. Независимые переменные называют также регрессорами или предикторами, а зависимые переменные – критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения между ними.
Цели регрессионного анализа: 1. Определение степени обусловленности вариации зависимой переменной изменением предикторов (независимых переменных); 2. Предсказание значения зависимой переменной с помощью независимых (одной или нескольких), т.е. построение математической модели поведения критериальной переменной в зависимости от изменения переменных-предикторов; 3. Определение вклада отдельных независимых переменных (предикторов) в вариацию зависимой переменной. Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа. Т.о., регрессионный анализ относится к методам математического моделирования. Подобный вид анализа является технически сложным и почти никогда не производится вручную – все необходимые операции выполняет программа статистической обработки данных.
Различают следующие разновидности регрессионного анализа: 1. Однофакторный (один независимый признак) и многофакторный (два и более независимых признака); 2. Линейный (моделируется полиноминальная функция первой степени) и нелинейный (моделируются более сложные функции – логит, пробит, пропорциональных рисков по Коксу, экспоненциальная регрессия и т.п.).
Классический регрессионный анализ не предусматривает использования количественных дискретных и качественных признаков – в анализ могут включаться только количественные непрерывные переменные (но есть специальные модификации, позволяющие работать и с дискретными, и с порядковыми признаками). Результат регрессионного анализа – построение регрессионного уравнения с наибольшим коэффициентом детерминации (R2).
1. Однофакторный линейный регрессионный анализ (простая регрессия) – один из вариантов двумерного статистического анализа. Критерии применимости однофакторного линейного регрессионного анализа: 1. Число наблюдений в исследуемой выборке (n) должно быть в несколько раз больше числа независимых признаков; 2. Все анализируемые признаки должны быть количественные, непрерывные и нормально распределенные; 3. Каждому значению Х (т.е. независимого признака) должно соответствовать только одно значение Y (т.е. зависимого признака); 4. В случае множественного регрессионного анализа необходимо также отсутствие линейных корреляций между независимыми признаками (т.н. «отсутствие мультиколлинеарности объясняющих признаков»).
Формула простой линейной регрессии имеет вид: Y = a + bX, Y – значение зависимой переменной; X – значение независимой переменной; где а – константа, при необходимости вводимая программой статистической обработки (т.н. «свободный член»); b – коэффициент при аргументе (независимой переменной).
Соответственно, результат выполнения однофакторного линейного регрессионного анализа – вычисленные величины свободного члена и коэффициента при аргументе. Качество построенной математической модели характеризуется показателем р (должен быть меньше или равен заранее оговоренному уровню значимости), а также коэффициентом детерминации R2 (должен максимально приближаться к единице). Напоминаем, что R2×100 (%) – это т.н. доля объясненной дисперсии, о которой шла речь ранее. Смысл данного понятия в том, что изменение признака Х приводит к изменению признака Y в R2×100 процентах случаев.
2. Многофакторный линейный регрессионный анализ (множественная регрессия) – способ анализа связи между несколькими независимыми переменными и зависимой переменной, выражающий данную связь в виде уравнения множественной линейной регрессии:
Здесь: Y – значение зависимой переменной; а – константа, при необходимости вводимая программой статистической обработки (т.н. «свободный член»); b1…n – коэффициент при аргументах (независимых переменных) X1…n; X1…n – значения соответствующих независимых переменных (№1, 2 и т.д., вплоть до n).
Критерии применимости многофакторного линейного регрессионного анализа такие же, как и однофакторного (см. выше). Результат выполнения многофакторного линейного регрессионного анализа – вычисленные величины свободного члена и коэффициентов при всех введенных в уравнение аргументах. Качество построенной математической модели характеризуется показателем р (должен быть меньше или равен заранее оговоренному уровню значимости), а также коэффициентом детерминации R2 (должен максимально приближаться к единице).
3. Нелинейный регрессионный анализ («подгонка кривых») – способ анализа связи между одной или несколькими независимыми переменными и зависимой переменной, выражающий данную связь в виде уравнения какой-либо нелинейной функции. Различают два класса нелинейных регрессий: – регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; – регрессии, нелинейные по оцениваемым параметрам.
Примером регрессии, нелинейной по включаемым в нее объясняющим переменным, могут служить следующие функции:
– полиномы разных степеней (т.н. степенные функции):
Y = а + bX + cX2 (квадратичная, или параболическая функция) Y = а + bX + сX2 + dX3 (кубическая функция) Y = а + bX + сX2 + dX3 + eX4 и т.д.
Здесь: Y – значение зависимой переменной; а – константа, при необходимости вводимая программой статистической обработки (т.н. «свободный член»); b, с, d, e и т.д. – коэффициенты при аргументе (независимой переменной) X; X – значение независимой переменной;
– равносторонняя гипербола: Y = a + b/X (обозначения те же – см. выше).
– полулогарифмическая функция: Y = a + b×lnX
К регрессиям, нелинейным по оцениваемым параметрам, относятся функции:
– степенная: Y = aXb
– показательная: Y = abX
– экспоненциальная: Y = ea+bX, где e – т.н. число Эйлера, или основание натурального логарифма (≈2,718).
– гиперболическая (не равносторонняя): Y = a
– логистическая (S-образная, сигмоида): Y =
– обратная: Y =
Графики некоторых из перечисленных функций показаны на рис. 27:
Рис. 27. Графическое отображение различных (линейных и нелинейных) функций, применяемых при выполнении нелинейного регрессионного анализа («подгонки кривых»).
Пример результата успешно выполненного нелинейного регрессионного анализа приведен на рис. 28. В данном случае R2=0,999, а математическая модель соответствует функции полинома второго порядка (т.е. квадратичной функции).
Общие замечания по регрессионному анализу:
Цель выполнения регрессионного анализа – нахождение математической модели, наилучшим образом описывающей наблюдающуюся в эксперименте закономерность. Данная модель в дальнейшем может использоваться для предсказания поведения той или иной системы в зависимости от изменения некоторых контролируемых факторов, что может быть весьма полезно и в медицине (например, предсказание прогноза заболевания и возможности развития его осложнений по некоторым ключевым параметрам, отслеживаемым при поступлении пациента в стационар или на ранних этапах госпитализации). Хорошие математические модели могут лечь в основу разработки анкет, опросников и шкал для диагностики различных заболеваний и определения лечебной тактики.
Рис. 28. Результат успешного применения нелинейного регрессионного анализа (подгонки кривых). Функция полинома второго порядка (квадратическая, или параболическая) идеально описывает поведение отслеживаемого параметра.
Признаки «хорошей» модели: Обычно для построения «хорошей» работоспособной модели и сравнения ее с другими возможными моделями необходимо учитывать следующие свойства (критерии): Скупость (простота). Модель должна быть максимально простой. Данное свойство определяется тем фактом, что модель не отражает действительность идеально, а является ее упрощением. Поэтому из двух моделей, приблизительно одинаково отражающих реальность, предпочтение отдается модели, содержащей меньшее число объясняющих переменных. Единственность. Для любого набора статистических данных определяемые коэффициенты должны вычисляться однозначно. Максимальное соответствие. Уравнение тем лучше, чем большую часть разброса зависимой переменной оно может объяснить. Поэтому стремятся построить уравнение с максимально возможным скорректированным коэффициентом детерминации R2. Считается, что для хорошей модели значение R2 должно составлять не менее 0,93…0,95. Согласованность с теорией. Никакое уравнение не может быть признано качественным, если оно не соответствует известным теоретическим предпосылкам. Другими словами, модель обязательно должна опираться на теоретический фундамент, т.к. в противном случае результат ее использования может быть (и обязательно будет) весьма плачевным. Прогнозные качества. Модель может быть признана качественной, если полученные на ее основе прогнозы подтверждаются реальностью.
Важно также отметить, что результаты регрессионного анализа применимы только к тому интервалу значений данных, на котором они получены. Например, если в результате выполнения регрессионного анализа была построена математическая модель вероятности развития некоего заболевания в зависимости от величины определенных биохимических показателей, причем при построении модели были использованы данные биохимических тестов для лиц в возрасте 20-50 лет, то для лиц старше 50 и моложе 20 лет данную модель использовать некорректно. Аналогично, если построена математическая модель эпидемиологии некоего заболевания на основании отрывочных данных о заболеваемости, датированных 1960-2000 гг., то данную модель можно использовать для определения недостающих показателей заболеваемости только в пределах 1960-2000 гг., но не ранее 1960 г и не позднее 2000 г. Проще говоря, математические модели нельзя экстраполировать за пределы интервала значений переменных, использованных при их построении, а что получается при нарушении этого правила, показано на рис. 29.
– Как видишь, к концу следующего месяца у тебя будет более четырех дюжин мужей… – Постой, но ведь нужно использовать более двух точек данных??! – Упс, ты права… (все значительно хуже, чем представлялось сразу).
Рис. 29. Причина, по которой результаты регрессионного анализа применимы только к тому интервалу значений данных, на котором они получены. Проще говоря, вне указанного интервала описанная математической моделью закономерность может (хоть и не обязана) случайным образом отличаться от таковой в пределах интервала.
Анализ взаимозависимости качественных признаков (установление взаимосвязи между воздействием и исходом)
Качественные признаки не имеют количественной размерности, но можно учесть в числовой форме сам факт их наличия либо отсутствия (1 – есть, 0 – нету), а также подсчитать частоту встречаемости качественного признака в анализируемой выборке («риск») и сравнительную вероятность его обнаружения («шанс»). Напомним, риск определяется как отношение количества лиц в выборке, имеющих изучаемый признак, к общему количеству лиц под наблюдением (т.е. к размеру выборки), выражаемое в долях единицы либо процентах. Соответственно, величина риска выражается неким числом в интервале от 0 до 1 (или от 0 до 100%).
Риск в общем случае соответствует частоте встречаемости либо вероятности развития изучаемого признака. Именно риск обычно используется в отечественной научной литературе как характеристика вероятности наступления события либо распространенности признака.
Шанс определяется как отношение количества лиц в выборке, имеющих изучаемый признак, к количеству лиц в той же выборке, не имеющих данного признака. Соответственно, шанс – некоторое число между 0 и бесконечностью. Шанс приблизительно равен риску, если частота исследуемого признака либо события невелика.
Шанс с величиной N означает, что вероятность наступления некоего события в N раз выше, чем того, что данное событие не наступит.
Для оценки влияния каких-либо факторов на развитие интересующего исследователей исхода можно определять и шанс, и риск. Вначале составляется четырехпольная таблица, или таблица 2×2 (как описано в разделе 9 настоящей главы, см. таблицу 5):
Затем подсчитываются величины шансов и рисков по формулам:
Сравнение частоты развития исхода в различных группах (в общем случае – опытной и контрольной) производится путем вычисления относительных характеристик – относительного риска (relative risk, risk ratio, RR) и отношения шансов (odds ratio, OR) по формулам:
Подставляя в данные уравнения формулы для расчета величин рисков и шансов, приведенные выше, получаем:
В связи с характерным видом формулы для вычисления отношения шансов его еще называют «перекрестным отношением». Отношение рисков показывает, во сколько раз риск некоего события («исхода») в опытной группе больше или меньше, чем в контрольной. Соответственно, отношение шансов показывает, насколько шанс некоего события в опытной группе больше или меньше, чем в контрольной.
При простом сравнении между опытной (экспериментальной) и контрольной группами: 1. Отношение рисков либо шансов, равное 1, означает, что между опытной и контрольной группами нет разницы в вероятности либо, соответственно, шансе события; 2. Отношение рисков либо шансов, меньшее 1, означает, что в опытной группе изучаемые событие либо параметр встречаются реже, чем в контрольной; 3. Отношение рисков либо шансов, большее 1, означает, что в опытной группе изучаемые событие либо параметр встречаются чаще, чем в контрольной;
Поскольку логика научного эксперимента предполагает, что в опытной группе имело место некое исследуемое воздействие, отсутствующее в контрольной группе, RR или OR, превышающее 1, свидетельствует о наличии статистической взаимосвязи между данным воздействием (фактором) и учитываемым исходом, причем воздействие увеличивает вероятность развития исхода. Соответственно, RR или OR, меньшее 1, также свидетельствует о наличии статистической взаимосвязи между воздействием (фактором) и учитываемым исходом, причем воздействие уменьшает вероятность развития исхода. В такой ситуации можно сказать, что исследуемый фактор оказывает на подопытных лиц протективное воздействие, уменьшая у них вероятность развития соответствующего исхода. В том случае, если RR или OR равны 1, статистическая взаимосвязь между воздействием и исходом отсутствует.
Расчет отношений рисков и/или шансов широко используется при выполнении т.н. исследований вида «случай-контроль» (case-control studies), где как раз и требуется доказать либо опровергнуть взаимосвязь между неким воздействием и неким исходом (см. Главу III настоящего руководства, раздел 4). При этом принципиальной разницы, что именно вычислять – отношение рисков или отношение шансов, нет, но в западной научной литературе отношение шансов (odds ratio, OR) прижилось в качестве стандарта de facto, вероятно, вследствие многолетних культурных традиций западного общества, где смысл шанса близок и понятен всем, кто делает ставки любого рода (например, играет на бирже). При этом расчет отношений шансов либо рисков является простым, но одновременно и довольно грубым способом установления статистической взаимосвязи между воздействием и исходом, поскольку он не учитывает изменения объема исследуемой группы (выборки) в ходе исследования. Существуют гораздо более сложные, точные и изящные методы для выявления такой взаимосвязи и оценки ее выраженности – например, анализ выживаемости признака по Каплану-Мейер (product limit Kaplan-Meier estimation), который будет подробно рассмотрен в следующей главе настоящего руководства (именно, в Главе III, пункте 5).
Для установления статистической значимости отношений шансов и рисков необходимо вычисление верхнего и нижнего пределов их доверительного интервала (как правило – 95%).
1. Вычисление доверительного интервала для отношения рисков (RR, ОР):
Вначале подсчитывают фактор ошибки относительного риска по формуле:
Здесь 1,96 – константа, необходимая для расчета 95% доверительного интервала (см. раздел 5 настоящей главы). Для 99% ДИ эта константа будет равна 2,58, а для 99,9% – 3,28.
Затем вычисляют верхний и нижний пределы доверительного интервала по формулам:
2. Вычисление доверительного интервала для отношения шансов (OR, ОШ):
Вначале подсчитывают фактор ошибки отношения шансов по формуле:
Здесь 1,96 – константа, необходимая для расчета 95% доверительного интервала (см. раздел 5 настоящей главы). Для 99% ДИ эта константа будет равна 2,58, а для 99,9% – 3,28.
Затем вычисляют верхний и нижний пределы доверительного интервала по формулам:
В том случае, если отношение шансов либо рисков >1, а нижний предел рассчитанного доверительного интервала ≤1, изучаемый фактор не может быть статистически значимой причиной интересующего нас исхода. Обратно этому, если отношение шансов либо рисков >1, но при этом нижний предел доверительного интервала также >1, данный фактор (воздействие) может быть причиной изучаемого исхода, поскольку их взаимосвязь статистически значима. Если же отношение шансов либо рисков <1, и верхний предел вычисленного ДИ также <1, то изучаемый фактор оказывает статистически значимое протективное влияние, предотвращая появление интересующего нас события (исхода). Когда отношение шансов либо рисков <1, а верхний предел вычисленного ДИ >1, то изучаемый фактор не оказывает статистически значимого протективного влияния на развитие интересующего исследователей события (исхода). Вывод о наличии клинически значимого влияния изучаемого фактора (воздействия) на интересующий исследователей исход делается, если вычисленные величины OR или RR достаточно велики (обычно >2 или <0,5).
Анализируя отношения шансов и рисков, полученные для различных воздействий, предположительно связанных с изучаемыми исходами, необходимо помнить о т.н. «смешивании эффектов» (confounding). Данный феномен наблюдается в том случае, если изучаемое воздействие (А) и интересующий исследователей исход (В) вместе определяются каким-либо неизвестным фактором С. Указанный фактор называется «вмешивающийся» (confounder). При этом интересующий нас исход очевидным образом не связан с изучаемым воздействием, но проведение вышеописанных вычислений может показать не только значительную величину OR (RR), но и пределы соответствующих им доверительных интервалов, отвечающие критериям статистической значимости (см. выше), что приведет к ложному заключению о наличии прямой взаимосвязи; иногда выявляемые таким образом «зависимости» поражают исследователей своей неожиданностью, парадоксальностью и «необъяснимостью». Как пример курьезных выводов, получаемых из-за «смешивания эффектов», можно привести исследование, где доказывается, что частота урогенитального хламидиоза у скейтбордистов достоверно выше, чем у лиц, не имеющих скейтборда [28]. На самом деле наличие скейтборда не оказывает никакого влияния на заболевания, передаваемые половым путем; просто оба факта «наличие скейтборда» и «инфицирование урогенитальным хламидиозом» зависят от не включенного в исследование критерия «изучаемое лицо – молодой мужчина с физической активностью выше средней». Если провести аналогичный анализ, набрав в контрольную группу только молодых, физически здоровых и активных мужчин в возрасте от 18 до 23 лет, не имеющих скейтборда, всякая разница в заболеваемости хламидиозом исчезнет.
|
