Когортные исследования
Данные исследования обладают большой доказательной силой и широко используются исследователями США и стран Западной Европы. Эти исследования основаны на наблюдении и не предполагают активного вмешательства исследователей в естественное течение изучаемого процесса; они также всегда являются «продольными», и почти всегда – проспективными (бывают и ретроспективные когортные исследования). Основная цель когортных исследований – установить, влияет ли определенное воздействие (или несколько) на последующее развитие определенного исхода (например, клинически манифестного заболевания). Кроме того, исследования подобного типа предпринимаются для точного описания типичного течения и характерных осложнений различных заболеваний, частоты встречаемости каких-либо событий, интересующих ученых, изучения побочных эффектов и взаимодействия лекарственных препаратов, выявления факторов риска различных заболеваний и состояний и оценки степени их вклада в развитие изучаемого исхода и т.п. Это лучший вид клинических исследований для тех случаев, когда эксперимент невозможен. Принцип когортных исследований – в продолжительном наблюдении за одной (реже – несколькими) группами исследуемых лиц (эти группы и называют «когорты»). Срок наблюдения варьирует от нескольких месяцев до десятков лет и оговаривается заранее (хотя в дальнейшем может быть при необходимости увеличен – в соответствии с результатами промежуточных анализов полученных данных). Размер когорты обычно стараются сделать как можно большим; в идеале когорта совпадает по численности с исследуемой генеральной совокупностью. В случае, если исследуется широко распространенное заболевание или состояние, представляющее большую социальную значимость, и все случаи таких заболеваний тщательно регистрируются на государственном уровне, описанный выше идеальный вариант достижим практически; так, ученые ряда стран исследуют национальные когорты ВИЧ-инфицированных или больных атеросклерозом. При согласованном объединении когорт нескольких стран образуются огромные интернациональные когорты; как правило, так поступают при организации больших международных мультицентровых исследований. Примером такого исследования является EuroSIDA, согласованно проводимая на 6 когортах ВИЧ-инфицированных, проживающих во многих странах Евросоюза, включая Польшу и страны Балтии, а также в России, Белоруссии и на Украине; общий размер объединенной когорты – более 11.200 больных [39]. Другим примером мультицентрового когортного исследования является D:A:D – The Data Collection on Adverse events of Anti-HIV Drugs (сбор данных о побочных эффектах антиретровирусных препаратов). Объединенная когорта данного исследования включает 11 национальных когорт ВИЧ-инфицированных лиц, проживающих в 21 европейской стране, а также в США и Австралии и наблюдающихся в 188 клиниках; суммарный размер данной когорты составляет 23.468 больных (данные на 2003 г.) [27]. Если в когорту удалось (или планируется) включить всех зарегистрированных больных с изучаемой патологией, она называется регистром. Регистр может быть региональный, национальный и (в основном для редких заболеваний) – международный; как пример можно привести регистр больных с острым коронарным синдромом Global Registry of Acute Coronary Events (GRACE) [20, 18], его приблизительным аналогом в России является регистр ОКС РЕКОРД (www.acs-registry.ru). Чем больше размер когорты, тем точнее получаемые данные и тем ближе они приближаются к таковым в генеральной совокупности; при этом пропорционально возрастает стоимость исследования и сложность его организации. Большие мультицентровые когортные исследования по силам только большим интернациональным научным коллективам при поддержке влиятельных спонсоров, как правило – фармацевтических компаний. Когортные исследования бывают фиксированные (после достижения определенного размера когорты включение в исследование новых пациентов прекращается) и динамические (возможно пополнение когорты новыми участниками в ходе наблюдения). Лица, включенные в когорту, находятся под наблюдением до проявления у них изучаемого исхода (outcome, endpoint). Исходом может быть, например, развитие какого-либо заболевания либо его осложнения, выздоровление или смерть больного, неудача лечения, появление побочного эффекта терапии; такие исходы называют истинными, поскольку они отражают реальные клинически значимые события в жизни исследуемого лица. Кроме того, бывают суррогатные исходы – обычно достижение определенного уровня каким-либо показателем, полученным при лабораторных либо инструментальных исследованиях (например, уровня CD4+ лимфоцитов, вирус-нагрузки плазмы крови, холестерина и т.п.). Суррогатные исходы косвенно указывают на развитие тех или иных истинных исходов (например, неудачи лечения или обострения заболевания), но сами таковыми не являются, поскольку представляют собой лишь симптом, вырванный из контекста общего патологического процесса; как правило, они неспецифичны для изучаемого состояния. В целом, не рекомендуется использовать суррогатные исходы вместо истинных; тем не менее, их применение возможно, если достоверно известно, что суррогатный исход надежно коррелирует с истинным и полностью отражает влияние изучаемого воздействия на клинический исход. Одновременно может анализироваться несколько исходов; в этом случае выделяют более важные первичные исходы (например, развитие заболевания, выздоровление или смерть больного) и менее важные вторичные (нередко – суррогатные: достижение пороговых уровней тех или иных лабораторных показателей, отказ от терапии, завершение курса лечения, появление побочных эффектов терапии и т.д.). Первичные исходы должны соответствовать основной цели проводимого исследования. Два или более независимых события, последовательного или одновременного наступления которых ждет исследователь, могут объединяться в т.н. составной (composite) исход (например, развитие СПИДа и/или смерть больного). Классическое когортное исследование строится по схеме, показанной на рис. 1. При анализе результатов когортных исследований наиболее часто используется метод анализа времени до наступления исхода (также называется «анализ вероятности наступления изучаемого исхода в определенный период времени» или «анализ выживаемости»). Кроме того, можно косвенно оценить влияние тех или иных факторов (по отдельности и вместе) на проявление регистрируемого события (исхода).
Рис. 1. Классическая схема когортного исследования (по материалам Royal Free & University College Medical School, London, 2005).
При этом корректные результаты могут быть получены только при анализе синхронизированной когорты, т.е. такой когорты, каждый из членов которой был включен в исследование в строго определенный и одинаковый для всех момент развития своего заболевания / состояния. Это может быть наступление определенной стадии заболевания по клиническим, лабораторным или клинико-лабораторным признакам, первичное проявление симптомов заболевания или его обострение, факт госпитализации, начала лечения, оперативного вмешательства и т.п. Данное условия требует тщательной формулировки критериев включения участников в исследование; в дальнейшем эти критерии должны неукоснительно соблюдаться. Когорта не обязательно должна формироваться одномоментно, но следует иметь в виду, что больные, включенные в исследование в разное время, могут быть несопоставимы по ряду признаков. Например, в случае хронических инфекционных заболеваний (вирусные гепатиты В, С, ВИЧ-инфекция и т.п.) методы диагностики и лечения достаточно быстро улучшаются с течением времени; в этой связи, если сравнить больных, включенных в исследование 15 лет назад и в настоящий момент, то окажется, что у современных больных заболевание было выявлено на более ранней стадии, а прогноз (и, соответственно, выживаемость к определенному сроку) существенно лучше, чем 15 лет назад, из-за радикального улучшения терапевтических подходов. Систематическая ошибка данного рода, связанная с улучшением методов диагностики и лечения по ходу продолжительного исследования, называется «ошибка временного сдвига» (lead-time bias); примером такой ошибки является исследование выживаемости ВИЧ-инфицированных больных, заболевание у которых было выявлено до и после 1985 г., из которого ожидаемо следует, что у больных, выявленных до 1985 г., выживаемость ниже [38]. Аналогично, при исследовании выживаемости ВИЧ-инфицированных лиц на фоне ВААРТ, начатой при различных уровнях CD4+ лимфоцитов (50 клеток/мм3 и 350 клеток/мм3, соответственно) оказалось, что при начале ВААРТ на фоне выраженной иммуносупрессии (50 клеток/мм3) выживаемость больных существенно ниже по сравнению с исходно высоким уровнем CD4+ лимфоцитов; при этом исследователи не учли, что процесс снижения уровня Тh-лимфоцитов с 350 до 50 клеток/мкл занимает несколько (2-7) лет, которые стоило бы приплюсовать к вычисленной выживаемости лиц с глубоким иммунодефицитом [38]. Данный пример также подчеркивает необходимость синхронизации формируемой когорты по ключевым показателям, способным оказать критическое влияние на предполагаемый результат исследования. Другой систематической ошибкой, которая может быть связана с исследованиями подобного рода, является т.н. ошибка дожития (survivorship bias). Данная ошибка возникает в случае, если сравнивается выживаемость больных, получавших или не получавших определенную терапию, причем анализируемый метод лечения стал доступен для использования на определенном этапе уже проводимого когортного исследования. В этом случае для того, чтобы подвергнуться определенному лечению, больные должны были дожить до его введения в клиническую практику, а все больные, умершие до этого момента, не имели шанса получить указанную терапию. Соответственно, оказывается, что лечение получили больные, у которых прогноз заболевания исходно был наиболее благоприятным, и в результате эффективность оцениваемой терапии может быть существенно завышена [38]. В целом, для обеспечения корректности анализа выживаемости необходимо соблюдение следующих условий: 1) выборка лиц, вошедших в когорту, случайна и репрезентативна; 2) наблюдения независимы; 3) в период исследования не происходило изменений в методах диагностики, лечения и процедурах наблюдения (т.е. критерии включения не изменялись); 4) в период исследования для всех больных, входящих в когорту, вероятность наступления изучаемого исхода не изменялась; 5) случаи смерти, выбывания из исследования и включения новых больных в когорту происходили более или менее равномерно на всем периоде наблюдения [6].
Для оценки влияния каких-либо факторов на развитие изучаемого исхода определяют следующие численные показатели:
1) Риск наступления изучаемого события (исхода) к моменту Х (risk of event by time t)
Риск - некоторое число в интервале между 0 и 1.
2) Шанс наступления изучаемого события (исхода) к моменту Х (odds of event by time t)
Шанс – некоторое число между 0 и бесконечностью. Шанс приблизительно равен риску, если частота исследуемого события (исхода) невелика; соответственно, чем реже встречается событие, тем больше величина шанса приближается к величине риска.
3) Частота наступления события (исхода) – incidence rate (также просто incidence или просто rate)
Частота события – некоторое число между 0 и бесконечностью, может быть выражена в любых единицах времени (дни, недели, месяцы, годы).
Сумма человеко-лет под наблюдением (person-years at risk) – это сумма времени, проведенного всеми участниками исследования под наблюдением в ожидании наступления изучаемого события (как бы общее число лет, проведенных всеми участниками исследования с риском наступления изучаемого исхода).
где n – общее количество лиц в когорте, а tn – время, проведенное участником n под наблюдением исследователей; суммируется число лет, проведенных под наблюдением каждым из участников исследования (независимо от того, наблюдались ли они весь срок исследования, или вышли из него, не дожидаясь окончания). Данное высказывание иллюстрируется нижеприведенным рисунком (см. рис. 2), на котором изображен принцип учета человеко-лет, проведенных под наблюдением участниками когортного исследования.
№ участника = исход под наблюдением 1 0,8 2 2,0 3 1,7 4 1,3 5 2,0 6 2,0 7 2,0 8 0,8 9 2,0 10 1,2 11 2,0 12 2,0 13 2,0 14 0,9 15 0,4 16 2,0 17 2,0 18 1,6 19 2,0 20 0,6 21 2,0 22 1,4 34,7 человеко-лет
начало окончание исследования исследования
Рис. 2. Принципы учета человеко-лет в когортном исследовании, а также принятый способ обработки неполных данных наблюдений в случае, если участник когорты вышел из исследования до его завершения по любым причинам (исключая наступление ожидаемого исхода).
Определение частоты события предпочтительнее, чем оценка риска или шанса, поскольку при этом учитывается тот факт, что не все члены когорты находятся под наблюдением в течение одинакового временного интервала. Если какой-либо из наблюдаемых индивидуумов вышел из исследования до его завершения по любым причинам (кроме наступления ожидаемого исхода), считается, что время до наступления исхода в данном случае цензурировано моментом последнего планового осмотра данного лица (см. рис. 2). Такое наблюдение называется неполным, незавершенным или цензурированным. К неполным относятся также те наблюдения, в которых изучаемый исход не наступил на момент окончания исследования. Полным, завершенным или нецензурированным считается такое наблюдение, в котором изучаемый исход наступил до окончания исследования, и при этом точно известен интервал времени между наступлением исхода и включением больного в исследование. В случае цензурированных наблюдений интервал времени с момента включения до наступления исхода неизвестен, зато точно известен интервал времени между включением и выбытием наблюдаемого лица из исследования. Данный интервал называется «время до отказа» (time to failure). Частота события - величина постоянная для всего периода исследования, т.к. вычисляется на основании суммарных данных за весь период (так, для ситуации, изображенной на рис. 2, частота исхода составляет 5÷34,7=0,14 на 1 человеко-год). В то же время ясно, что вероятность появления ожидаемого исхода на разных временных отрезках неодинакова и с течением времени может закономерно изменяться (например, вероятность умереть возрастает пропорционально возрасту, начиная приблизительно с 40 лет). Вероятность развития интересующего нас исхода в данный момент времени характеризуется показателем, называемым «частота (потенциальной) опасности события» (event hazard rate).
4) Частота (потенциальной) опасности события (event hazard rate) вычисляется как отношение числа лиц с ожидаемым исходом, развившимся за интересующий нас отрезок времени (определенный день, неделю, месяц, год) в пределах общего срока исследования к количеству человеко-лет (месяцев, недель, дней), проведенных под наблюдением всеми наличными участниками исследования на данном временном отрезке. Размерность частоты риска события соответствует использованной единице времени.
5) Собственно сравнение частоты развития исхода в различных группах внутри когорты, выделенных по факту наличия и/или отсутствия признака (признаков), влияние которых на исход изучается в данном исследовании (например, в группах мужчин и женщин, леченных и нелеченных, получавших схему лечения А и схему лечения В, подвергшихся и не подвергшихся воздействию факторов риска и т.д.) производится при помощи вычисления относительных характеристик – относительного риска (также отношения рисков – relative risk, risk ratio) и отношения частот (rate ratio). Также может рассчитываться отношение шансов (odds ratio).
Величины отношения шансов и относительного риска практически совпадают, если количество наблюдаемых исходов мало, а размер когорты велик.
Доверительный интервал для относительного риска (risk ratio) вычисляется почти так же, как для отношения шансов (см. описание исследований вида «случай-контроль»). Вначале подсчитывают фактор ошибки относительного риска:
где: a – число лиц с искомым исходом в группе 1; b – число лиц с искомым исходом в группе 2.
При использовании коэффициента 1,96 производится расчет 95% доверительного интервала, т.е. в такой интервал значение отношения рисков в генеральной совокупности попадает с 95% вероятностью.
Затем вычисляют верхний и нижний пределы доверительного интервала:
Доверительный интервал для отношения частот (rate ratio) вычисляется точно так же, по тем же формулам, что и для относительного риска.
Напомним, что 95% доверительный интервал для отношения шансов (odds ratio) в когортных исследованиях вычисляется следующим образом:
где: a – число лиц с искомым исходом в группе 1; b – число лиц с искомым исходом в группе 2; c – число лиц в группе 1, у которых исход не наступил; d – число лиц в группе 2, у которых исход не наступил.
Результатам когортных исследований о влиянии каких-либо факторов на частоту появления определенного события можно доверять, если: 1) выявленное влияние изучаемого фактора на регистрируемый исход велико (относительный риск, отношение частот, отношение шансов >2 или <0,5); 2) аналогичные результаты получены более чем в двух независимых исследованиях; 3) систематические ошибки и явление «смешивания эффектов» при наборе когорт, наблюдении за участниками исследования и анализе результатов отсутствуют, либо систематические ошибки имеются, но в разных исследованиях они имеют различную направленность (т.е. неодинаковы).
6) Время-зависимая относительная опасность (time-specific relative hazard) - отношение частоты опасности события (event hazard rate) в одной группе к частоте опасности события в другой сравниваемой группе, при условии, что частоты в обеих группах рассчитаны для одного и того же временного интервала. Относительная опасность, или отношение опасностей (relative hazard, hazard ratio) - средняя арифметическая всех время-зависимых относительных опасностей, последовательно рассчитанных для всех временных отрезков настоящего исследования. Продолжительность же временных отрезков произвольно устанавливается исследователями в соответствии с целями научной работы. Обычно данная продолжительность устанавливается равной промежутку времени между плановыми обследованиями (follow-ups) членов когорты. При расчете всех разновидностей относительных опасностей исходно предполагается, что истинная относительная опасность одинакова и постоянна в каждой временной точке анализируемого периода.
Оценка времени до наступления ожидаемого исхода также называется «анализ вероятности наступления изучаемого исхода в определенный период времени» или «анализ выживаемости». Обычно данная оценка производится по методике Каплана-Мейера (Kaplan-Meier estimation). Для описания принципа применения указанной методики вновь воспользуемся примером, приведенным на рис. 2.
Вначале строится таблица следующего вида:
Из таблицы видно, что число лиц под наблюдением без исхода (см. колонку №2) уменьшается всякий раз после регистрации очередного исхода или выхода члена когорты из исследования (регистрации неполного, или цензурированного, наблюдения) на суммарное число лиц, покинувших исследование за рассматриваемый временной интервал (исходы + неполные наблюдения), причем указанное уменьшение регистрируется начиная со следующего за текущим временного интервала. Наиболее удобно вначале заполнять колонки №3 и №4 («количество развившихся исходов…» и «количество неполных наблюдений…»), после чего значительно проще производить заполнение колонки №2 («число лиц под наблюдением без исхода…»). В колонках №3 и №4 указываются только те исходы и цензурированные наблюдения, которые были отмечены за текущий интервал времени; размер временного интервала выбирается произвольно, исходя из нужд исследователей и цели исследования. Обычно продолжительность временных интервалов устанавливается равной промежутку времени между плановыми обследованиями (follow-ups) членов когорты, причем собственно момент обследования разграничивает соседние интервалы. Именно поэтому лица, выбывшие из исследования по разным причинам, учитываются начиная с отрезка времени, следующего за тем, во время которого состоялся выход данных лиц из состава когорты (см. колонку №2 таблицы, «число лиц под наблюдением без исхода…»). Все наблюдения, в которых ожидаемый исход не был зафиксирован к моменту окончания исследования, считаются цензурированными, что и отражено в последней ячейке колонки №4 («количество неполных наблюдений…»). Если участник исследования по каким-либо причинам (кроме регистрации ожидаемого исхода) покинул когорту до окончания исследования, такое наблюдение считается цензурированным по времени последнего планового осмотра указанного лица (т.е. последним эпизодом наблюдения за данным членом когорты считается момент последнего планового осмотра, во время которого не было зафиксировано ожидаемого исхода; отрезок времени с момента последнего осмотра до момента выхода (де-юре или де-факто) больного из состава когорты отбрасывается). После расчета кумулятивной вероятности отсутствия исхода вплоть до момента завершения исследования (последняя колонка в таблице) производится построение графика Каплана-Мейера, который отражает вероятность отсутствия изучаемого исхода у членов когорты с момента начала исследования вплоть до момента его окончания включительно (рис. 3).
Рис. 3. График Каплана-Мейера, построенный для примера, приведенного на рис. 2. Указанный график построен при помощи пакета прикладных программ для статистических расчетов Statistica 7.0 (Функция Advanced linear/nonlinear models → Survival analysis → Kaplan & Meier product-limit method).
Видно, что график Каплана-Мейера представляет собой серию «ступенек», где снижение кумулятивной вероятности отсутствия исхода происходит скачкообразно после регистрации очередного случая (случаев) ожидаемого события; регистрация цензурированных наблюдений не приводит к снижению вероятности отсутствия исхода, вследствие чего «ступенька» на графике не образуется, но сам факт регистрации неполного наблюдения отмечается на графике специальным значком. Данная особенность построения графиков Каплана-Мейера напрямую вытекает из принципа организации когортных исследований, который подразумевает не непрерывный, а периодический учет изменений в состоянии членов когорты во время регулярных контрольных осмотров, вследствие чего изменение вероятности наличия либо отсутствия искомого состояния происходит не плавно, а скачками. Изображенная на графике Каплана-Мейера кривая называется кривой дожития. Две кривые дожития, полученные при анализе независимых групп, можно сравнивать, используя лог-ранговый тест (log rank test); если в результате вероятность нулевой гипотезы (р) оказывается равна или менее 0,05, то кривые дожития отличаются друг от друга с вероятностью 95% и более. Кривую дожития можно представить и в альтернативном виде – как кривую вероятности появления ожидаемого исхода к интересующему нас моменту времени. К сожалению, Statistica 7.0 не позволяет строить графики Каплана-Мейера в альтернативном представлении, но выглядеть он должен приблизительно следующим образом (рис. 4):
Рис. 4. График Каплана-Мейера, построенный для примера, приведенного на рис. 2, в альтернативном представлении (кривая вероятности появления ожидаемого события («исхода») с течением времени).
Следует обратить внимание на то, что вероятность развития исхода к моменту окончания исследования составляет примерно 26% (1 − 0,742), при этом риск наступления исхода к тому же моменту, рассчитанный по приведенной ранее формуле и имеющий тот же смысл, равен 5÷22 = 22,7%. Величина риска получилась заниженной, поскольку формула для его вычисления не предусматривает постепенное уменьшение размера когорты в ходе исследования (ввиду наступления исхода у части наблюдаемых лиц, а также вследствие выхода больных из состава когорты по другим причинам). Таким образом, применение методики Каплана-Мейера дает более точные результаты, чем просто расчет риска наступления события к интересующему моменту, ввиду чего данная методика является предпочтительной для обработки результатов когортных исследований. В случае, если продолжительность наблюдения очень велика (десятки лет), а изучаемые исходы регистрируются редко, для оси абсцисс можно использовать логарифмическую шкалу; так обычно поступают при исследованиях длительно текущих хронических заболеваний (ВИЧ-инфекция, хронические вирусные гепатиты, ишемическая болезнь сердца и т.п.).
Помимо построения графика Каплана-Мейера, анализ выживаемости подразумевает определение следующих показателей: 1) выживаемость (доля участников исследования, у которых искомый исход не наступил) для интересующего срока наблюдения; 2 ) стандартная ошибка кумулятивной выживаемости – рассчитывается при помощи соответствующей функции программы для статистического анализа (standard error of cumulative survival), в нашем примере – 0,0996 на момент окончания периода наблюдения; 3) суммарное число членов когорты для интересующего срока наблюдения; 4) медиана времени выживания (median survival time) – период времени, в течение которого изучаемый исход наступит у 50% участников исследования. Указанная величина соответствует медиане времени до наступления исхода (median time to event) в случае выбора альтернативного представления графика Каплана-Мейера, см. выше. Кроме того, указываются 25-й и 75-й процентили кривой дожития (т.е. первый и третий квартили). Следует учитывать, что медиана времени до наступления исхода, рассчитанная указанным способом, будет отличаться от величины с тем же названием, вычисленной на основе анализа времени до развития изучаемого состояния у лиц, уже имеющих данное состояние. В нашем примере медиану времени выживания указать невозможно, поскольку на момент окончания наблюдения более половины членов когорты не имели изучаемого исхода. Тем не менее, можно указать первый квартиль (25-й процентиль) кривой дожития – он равен 1,57 лет; именно к этому сроку изучаемое состояние разовьется у 25% испытуемых лиц. 5) поскольку кумулятивная вероятность отсутствия исхода («вероятность дожития») рассчитывается из данных выборки, более или менее репрезентативной, необходимо определить доверительный интервал для указанной величины, чтобы определить, в каких пределах лежит истинная вероятность дожития в генеральной совокупности. 95% доверительный интервал рассчитывается по следующей формуле:
где: Р – доля выживших (выживаемость) к интересующему сроку наблюдения; n – число лиц под наблюдением (т.е. размер когорты) к интересующему сроку; 1,96 – коэффициент, задающий точность расчета доверительного интервала.
Анализируя данные когортных исследований, необходимо помнить о возможности смешивания эффектов (confounding), подробно описанного в разделе «исследования вида случай-контроль». Кратко, указанное явление наблюдается в случае, если некий фактор А, учет и/или анализ которого в исследовании не производился, влияет как на развитие изучаемого исхода И, так и на проявление одного или нескольких факторов (Б, В, Г), учитываемых в данном исследовании. Внешне это выглядит, как если бы факторы Б, В, Г влияли на развитие исхода И, хотя на самом деле они с ним непосредственно не связаны. Например, факт употребления парентеральных наркотических средств увеличивает риск смерти; при этом может иметь место смешивание эффектов – парентеральные наркоманы почти всегда заболевают хроническим вирусным гепатитом С (неучтенный фактор), который, в свою очередь, увеличивает риск смерти. Факт наркомании как таковой также может увеличивать риск смерти индивидуума, но наличие неучтенного фактора (ХВГС) приводит к завышению степени данного увеличения. Возможность смешивания эффектов нельзя полностью учесть на этапе планирования исследования, поскольку невозможно учесть вообще все факторы, могущие представлять какую-либо значимость. До некоторой степени возможное смешивание эффектов можно нейтрализовать на этапе анализа данных исследования посредством проведения стратификации или статистического моделирования. Например, мы анализируем сравнительную эффективность схем антиретровирусной терапии А и В. Каждой из схем было пролечено по 1000 ВИЧ-инфицированных; отсутствие вирусологического ответа было отмечено у 300 человек, получавших схему А (30%), и у 450 человек, получавших схему В (45%), относительный риск неудачи лечения составил в данном случае 30÷45=0,67. Можно ли вести речь о том, что схема лечения А достоверно более эффективна, чем терапевтическая схема В? На самом деле в обеих группах имеется неучтенный фактор - количество лиц, впервые получающих антиретровирусную терапию (т.е. «АРТ-наивных»). Известно, что у лиц, ранее получавших АРТ, эффективность последующих схем существенно снижается с каждой очередной сменой терапии. Ввиду этого, учет указанного фактора критически важен для анализа результатов данного исследования. Оказывается, в группе, пролеченной по схеме А, АРТ-наивных лиц было 800 (80%), а в группе, пролеченной по схеме В – 200 (20%), т.е. при формировании исследуемых групп рандомизация по этому признаку не проводилась. Для «подгонки» (adjustment) результатов статистических выкладок по данному фактору необходимо обратиться к базе данных исследования и выяснить частоту вирусологической неудачи лечения отдельно для АРТ-наивных лиц и больных, получавших АРТ более одного раза, для каждой из двух анализируемых групп. Требуемые данные приведены в нижеследующей таблице:
Из таблицы видно, что в обеих группах пропорция лиц с вирусологической неудачей лечения одинакова как среди АРТ-наивных лиц, так и среди ВИЧ-инфицированных, ранее уже получавших АРТ; в обоих случаях относительный риск равен 1,0. Относительный риск после стратификации («расслоения») анализируемых групп по факту получения АРТ до начала настоящей терапии вычисляется как среднее арифметическое величин относительного риска в обеих подгруппах, и, соответственно, тоже оказывается равным 1, т.к. (1+1)÷2=1. В итоге приходится признать, что на самом деле схемы лечения А и В обладают одинаковой эффективностью, а полученная в исследовании разница обусловлена только лишь ошибкой при формировании изучаемых групп, которые не были рандомизированы по фактору, оказывающему существенное влияние на результат интересующего нас вмешательства. Важно помнить, что при стратификации неизбежно уменьшается размер сравниваемых групп, что ведет к существенному снижению статистической значимости исследования. При анализе данных когортного исследования по Каплану-Мейеру (в том числе при сравнении кривых дожития лог-ранговым тестом) выполнить стратификацию по «вмешивающемуся» фактору невозможно, и, следовательно, смешивание эффектов должно быть по возможности учтено и устранено на этапе планирования эксперимента. Для того, чтобы учесть при анализе наличие нескольких «вмешивающихся» эффектов одновременно, используют построение статистической (регрессионной) модели с переменными параметрами. Выбор разновидности регрессионной модели зависит от особенностей изучаемого исхода: если ожидаемый исход – факт наступления некоего события / развития определенного состояния (оцениваемый в категориях «да/нет») – используется логистическая регрессия (logistic regression), в случае же, если изучается время, прошедшее до наступления того или иного события / развития определенного состояния, применяются регрессия Пуассона (Poisson regression) либо регрессия пропорциональных рисков по Коксу (Cox proportional hazard, Cox regression). Следует понимать, что построение регрессионных моделей используется для выявления множественных «вмешивающихся» эффектов (confounders) и оценки их влияния на развитие изучаемого исхода. В случае, если сравниваемые группы на этапе их формирования были должным образом рандомизированы и сбалансированы по всем существенным показателям, нужды в применении регрессионного анализа нет.
Отдельной проблемой является интерпретация и учет неполных (цензурированных) наблюдений, поскольку до настоящего времени среди исследователей нет единого мнения об универсальных принципах выполнения данной задачи [1]. Здесь существует три конкурирующих подхода: 1) Цензурирование справа и/или усечение слева (right-censoring / left-truncation); 2) Интервальное цензурирование (interval-censoring); 3) В особых случаях может применяться цензурирование слева (left-censoring).
Цензурирование справа применяется в том случае, если исследователям точно известна дата и время наступления ожидаемого исхода у каждого из подопытных членов когорты. Данная ситуация имеет место в случае, когда изучаются некие острые заболевания или состояния, отчетливо проявляющиеся клинически (например, инфаркт миокарда, инсульты, острые респираторные заболевания и т.п.). Усечение слева – элемент цензурирования справа и применяется в том случае, если изучаемые лица были включены в когорту в ходе исследования и наблюдались не с момента его начала, либо имели один или несколько промежуточных исходов на момент включения в когорту. Об интервальном цензурировании говорят, когда известно лишь, что изучаемый исход наступил в пределах определенного временного интервала, обычно – между двумя смежными плановыми осмотрами больного. Такая ситуация является типичной для исследований хронических или подостро текущих состояний без ярких клинических проявлений (например, ВИЧ-инфекции, хронических бронхо-легочных заболеваний, атеросклероза, сравнения эффективности терапевтических схем и т.п., когда наступивший исход регистрируется в первую очередь по данным лабораторно-инструментальных методов обследования). Для анализа данных, к которым применимо цензурирование справа, могут применяться все вышеперечисленные методы вычислений (методика Каплана-Мейера, сравнение кривых дожития лог-ранговым тестом, «подгонка» по «вмешивающимся» факторам с использованием регрессии Кокса либо регрессии Пуассона, расчет частоты исходов и т.п.). В случае, когда исследователи вынуждены иметь дело с интервальным цензурированием, применяются два основных подхода 1) Использовать какой-либо из методов аппроксимации (приближения) времени наступления исхода для того, чтобы свести интервальное цензурирование к цензурированию справа, после чего использовать простые методы вычислений, описанные выше; 2) Использовать альтернативные методы математического анализа, изначально пригодные для работы с интервальным цензурированием. Данный подход должен учитывать две возможные ситуации: а) Интервал между двумя смежными осмотрами для всех членов когорты одинаков; б) Имела место различная продолжительность интервалов между осмотрами.
Для выполнения аппроксимации пользуются следующими методиками: 1) Если известно, что исход наступил в интервале между моментами времени А и В, то можно допустить, что это произошло в средней точке данного временного интервала:
2) Можно принять за условное время наступления исхода любую воображаемую точку в пределах данного интервала при условии, что данное правило будет систематически применено ко всем интервалам времени в пределах общего срока наблюдения. Так, выше рекомендовалось считать дату планового осмотра, при котором был выявлен изучаемый исход, условным моментом наступления означенного исхода.
Кроме аппроксимации, можно использовать методику предсказания времени наступления события. В случае, когда все члены когорты проходили осмотры в одно и то же время tn, где n – порядковый номер осмотра, то: qn – вероятность того, что событие, не имевшее место в момент tn, также не имело место в момент tn-1; S(tn) – вероятность, что событие не произошло в момент tn;
S(tn) = q1 × q2 … × qn
Параметры q1, q2 и т.д. устанавливаются исходя из принципа максимальной вероятности (maximum likelihood). Этот принцип гласит: «Представьте реально наблюдаемую частоту события как функцию q1, q2, … qn, а потом подберите такие значения q1, q2… qn, которые дают максимальное значение данной функции». Например, в случае, если мы рассматриваем участника исследования, который во время первых трех осмотров не имел исхода, а в дальнейшем он развился, то будет наблюдаться следующая картина:
Наблюдаемая закономерность может быть выражена формулой:
Данная формула представляет собой оценочную функцию таблицы дожития (life-table = mortality table), и на основании вычисленных с ее помощью значений qn можно построить кривую дожития («выживаемости»). Стандартная ошибка qn вычисляется по формуле Гринвуда (Greenwood), включенной в большинство программ для статистического анализа. В качестве примера можно привести исследование выживаемости пациентов со злокачественной миеломой, где все наблюдения были сгруппированы по интервалам продолжительностью 1 год:
Дальнейший анализ данных идентичен таковому по методике Каплана-Мейера.
В рамках рассмотренной ситуации возможен случай, когда все члены когорты проходили осмотры в одно и то же время, но некоторые из них пропустили один или несколько осмотров. В этом случае таблица дожития примет следующий вид:
Участник №1:
Участник №2:
В данном случае неясно, наступил ли исход в интервале между t1 и t2 или между t2 и t3. Вынужденно приходится считать, что исход мог наступить в интервале t1-t2, вследствие чего вероятности отсутствия исхода к моментам t1, t2 и t2, t3 вычисляются по одинаковым формулам и суммируются (но не перемножаются!). Данное правило действует для тех случаев, когда наличие некоего исхода определенно исключает его отсутствие (exclusive event).
Участник №3:
Здесь ситуация в интервале между t3 и t5 аналогична рассмотренной в предыдущем примере, ввиду чего вероятность отсутствия исхода к моментам t3, t4 также вычисляется по вышеуказанной формуле.
Параметры q1, q2… qn, и, соответственно, кривая дожития могут быть установлены с использованием принципа максимальной вероятности; при этом можно использовать стандартные программные пакеты для статистического анализа.
В ситуации, когда интервалы между последовательными осмотрами различны для разных членов когорты, информация, полученная при наблюдении за каждым из участников исследования, складывается из суммы наблюдений по всем отдельно взятым интервалам. Число интервалов, и, соответственно, количество характеристик для каждого из них (qn, S(tn)) зависит от количества исследуемых лиц и особенностей их индивидуального графика обследований. При этом существует ряд технических проблем при вычислении стандартных ошибок из-за большого количества учитываемых параметров. Оценочная функция кривой дожития для данного случая известна как оценочная функция Турнбулла (Turnbull).
Возможен особый случай, называемый «цензурирование слева» (left-censoring, не путать с усечением слева!). В этом случае все исследуемые лица включаются в когорту в одно и то же время (т.е. наблюдаются с момента начала исследования), при этом их состояние в дальнейшем оценивается только один раз (т.е. в конце первого временного интервала), после чего производится анализ данных, независимо от наличия или отсутствия изучаемого исхода в каждом конкретном случае. Такая разновидность данных называется «данные о текущем состоянии» (current status data). В качестве примера можно привести исследование состояния здоровья беженцев, выполненное в Дании [1]. В течение 2,5 лет под наблюдением находилось 10.422 лица со статусом беженцев; все они оставались в центре Красного Креста все время, пока выносилось решение по их делам (от нескольких месяцев до нескольких лет). По убытии из центра они опрашивались и осматривались врачом на предмет наличия различных заболеваний, выявленные случаи регистрировались, но учет момента появления найденных заболеваний не производился. Требовалось подтвердить или опровергнуть гипотезу, согласно которой у беженцев, перенесших тюремное заключение или пытки, некоторые заболевания встречались чаще, чем у остальных. В данном случае стандартные методы сравнения оказались неприменимы из-за слишком большого количества учитываемых параметров. Вместо этого был использован метод, основанный на определении «площади под кривой дожития» (по Andersen & Ronn, 1995). При этом строились кривые вероятности развития того или иного заболевания отдельно для группы беженцев, подвергавшихся пыткам и/или тюремному заключению, и для остальных беженцев; переменная продолжительность единственного интервала наблюдения (от 1-2 месяцев до 2-3 лет) заменила собой несколько интервалов равной продолжительности. При этом ни в одном из наблюдений не был точно известен момент развития регистрируемых заболеваний. В итоге время, прошедшее с момента предполагаемого развития заболевания до момента прибытия в центр Красного Креста, пришлось просто отбросить и не учитывать при статистическом анализе (т.н. цензурирование слева). В дальнейшем определялась площадь под обеими кривыми дожития и производилось ее сравнение согласно методике. В частности, было установлено, что психические расстройства достоверно чаще встречались в группе лиц, ранее подвергавшихся пыткам и тюремному заключению (p<0,0001). Из других методов, применяющихся для анализа данных, полученных при интервальном цензурировании, следует упомянуть о построении параметрических кривых дожития. При этом предполагается, что кривые дожития имеют особую «параметрическую» форму, описываемую экспоненциальной функцией S(t)=exp(−λt) либо функцией Вейбулла (Weibull) S(t)=exp(−λtα), причем для определения параметров λ и α используется описанный выше принцип максимальной вероятности. Данный вид статистических расчетов доступен при использовании пакета прикладных программ SAS. Кроме того, не так давно [34, 19] было показано, что регрессия пропорциональных рисков по Коксу (Cox regression) может использоваться для построения модели кумулятивного риска (additive hazard model), которая, в свою очередь, может применяться для анализа данных о текущем состоянии. Важно отметить, что в исследованиях эпидемиологии инфекционных заболеваний интервальное цензурирование встречается наиболее часто.
В качестве типичного примера когортного дизайна можно привести исследование, выполненное на когорте больных гемофилией Бесплатного Королевского Госпиталя (Royal Free Hospital). В гематологическом отделении вышеупомянутой больницы наблюдалось 111 ВИЧ-инфицированных мужчин-гемофиликов, заразившихся в период с 1979 по 1985 гг., на предмет особенностей течения ВИЧ-инфекции у данной категории больных. Продолжительность наблюдения составила 25 лет. Учитывались демографические факторы, клиническая симптоматика, лабораторные данные, а также информация об эффективности лечения. На момент окончания исследования в живых остались 39 его участников, в том числе 28 – под непосредственным наблюдением в составе когорты [37]. Другим примером «классического» когортного исследования является мультицентровое исследование когорты лиц со СПИДом [44]. В течение двух вербовочных периодов (с апреля 1984 г. по март 1985 г. и с 1987 г. по 1991 г.) было рекрутировано несколько сотен ВИЧ-инфицированных гомосексуалистов, проживающих в 4 столичных областях США; в дальнейшем они проходили амбулаторное обследование каждые 6 месяцев. В процессе обследования собиралась демографическая информация (дата рождения, национальность), клинические данные (обследование на наличие признаков СПИДа при каждом осмотре, регистрация даты и причины смерти), лабораторные данные (подсчет уровня CD4+ лимфоцитов и количества копий РНК ВИЧ в плазме крови), сведения о проводимой терапии (даты начала и прекращения назначения всех антиретровирусных препаратов), а также некоторые другие данные (дата первого положительного обследования на ВИЧ-инфекцию, проводилась ли профилактика пневмоцистной пневмонии и т.п.). Еще одним образцом когортного дизайна является исследование частоты коинфекции ВИЧ и туберкулеза, проведенное в одном из госпиталей Нью-Йорка [47]. Первоначально 513 внутривенных наркоманов были обследованы на ВИЧ-инфекцию; 215 из них оказались ВИЧ-позитивными. Затем вся указанная когорта наблюдалась в течение 2 лет, при этом регистрировались любые признаки активного туберкулеза. Были получены следующие результаты: среди серопозитивных лиц (215) туберкулез развился у 8, среди серонегативных (298) – ни у одного из наблюдавшихся наркоманов, включенных в когорту. Риск развития туберкулеза в группе ВИЧ-позитивных лиц был оценен как 0,037 (соответственно, в группе ВИЧ-негативных лиц риск развития туберкулеза оказался равен нулю).
Когортный дизайн биомедицинских исследований имеет следующие преимущества: 1. Можно оценить временн у ю взаимосвязь между воздействием какого-либо фактора и развитием исхода (например, заболевания), поскольку всегда известен порядок следования регистрируемых событий; 2. На основании анализа данных, полученных в когортных исследованиях, можно попытаться установить причинно-следственные взаимосвязи между воздействиями и исходами (хотя рандомизированные контролируемые исследования в этом смысле предпочтительнее).
Недостатки когортного дизайна следующие: 1. Если исследуемый исход (например, заболевание) относится к редким явлениям, то размер когорты должен быть очень большим, а период наблюдения за ней - весьма продолжительным, что приводит к удорожанию всего исследования; 2. Вообще, когортные исследования занимают много времени и требуют вложения значительно б о льших средств, чем ранее описанные типы дизайна, что накладывает определенные ограничения как на максимальные размеры когорт, так и на продолжительность исследования; это особенно актуально для стран с невысоким уровнем ассигнований на науку (т.е. практически для всех стран Восточной Европы и постсоветского пространства); 3. Высокая вероятность систематических ошибок (biases) при сборе и анализе данных из-за описанного ранее явления «смешивания эффектов» (confounding) - ведь невозможно заранее знать, какие факторы являются существенными для развития интересующего исследователей исхода, и включить их регистрацию в план исследования; соответственно, оставшийся неучтенным фактор (факторы) может как обусловливать развитие изучаемого явления, так и взаимодействовать с регистрируемыми воздействиями, что приводит к эффектам, описанным выше (см. описание исследований вида «случай-контроль»); 4. Возможны проблемы с уменьшением статистической надежности исследования ввиду неизбежного уменьшения размера когорт в ходе исследования по неустановленным причинам (т.н. loss-to follow-up). Поскольку когортные исследования длятся годами и десятилетиями, члены когорты могут сменить место жительства, семейный статус, умереть, а также отказаться от наблюдения и выйти из исследования, не уточняя причин. При этом всякий раз желательно проверять, не связан ли выход конкретного лица из научного проекта с развитием интересующего исследователей исхода; особенно данное положение касается исследований т.н. «психотравмирующих» (scaring) заболеваний, в частности, ВИЧ-инфекции, парентеральных гепатитов и заболеваний, передающихся половым путем (ЗППП).
|


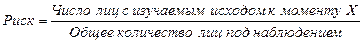


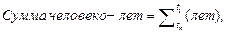
 = цензурировано Человеко-лет
= цензурировано Человеко-лет

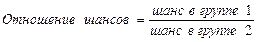
 ,
,

 ,
,