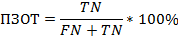Вычисление порогов отсечения для методов диагностики, оценка их диагностической ценности, ROC-анализ
Распространенная разновидность научных исследований – разработка и практическое внедрение новых методов диагностики. Статистическая обработка результатов подобных исследований достаточно специфична: 1. Необходимо сравнить результаты, полученные с использованием новой методики, с результатами применения существующих методов обследования и оценить направление и статистическую значимость имеющихся различий; 2. Необходимо определить значение оцениваемого параметра, при достижении которого будет приниматься решение о наличии патологии – т.н. точку отсечения (cut-off value); 3. Необходимо оценить диагностическую значимость новой методики и выразить ее в неких интегральных показателях, допускающих удобное сравнение эффективности предлагаемой методики с таковой у других известных методов обследования.
Для решения указанных задач разработан особый метод статистического анализа, называемый «ROC-анализ» (Receiver Operator Characteristic, т.е. «операционная характеристика приёмника», и не спрашивайте у меня, что это значит). ROC-анализ пригоден для описания характеристик диагностических методов, осуществляющих т.н. «бинарную классификацию», т.е. выявляющих наличие некоего состояния (условно обозначаемое «1») либо его отсутствие (условно обозначаемое «0»). К счастью, подобные методы диагностики преобладают в практической медицине, т.к. в основном задача любого диагностического исследования сводится к ответу на вопрос, болен или здоров исследуемый субъект. Соответственно, два варианта выявляемого состояния должны быть взаимоисключающими – либо, образно говоря, у пациента есть ВИЧ-инфекция, либо уж ее нет. Такая ситуация, когда наличие некоего исхода однозначно исключает его отсутствие, называется «исключительное событие» (exclusive event).
В основе ROC-анализа лежит описанное выше уравнение логистической функции, а сам анализ является специальной разновидностью логистической регрессии (см. предыдущий пункт настоящей главы). Напомним, уравнение логистической функции (также называемой S-образной, или сигмоидой: Y =
Множественный регрессионный анализ сам по себе можно использовать для оценки вероятности исхода любого события, вычислив стандартные коэффициенты регрессии, но здесь есть проблема: выходные значения большинства уравнений регрессионных функций не только являются непрерывными, но и выходят за пределы интервала [0…1], а нам нужны дискретные значения – 0 или 1, т.к. переменная отклика бинарна по своей природе. Таким образом, множественная регрессия игнорирует ограничения на диапазон значений для Y. Для решения проблемы задача регрессии может быть сформулирована иначе: вместо вычисления бинарной переменной мы вычисляем непрерывную переменную со значениями, лежащими на отрезке [0…1] при любых значениях независимых переменных. Это достигается применением специального регрессионного уравнения (т.н. логит-преобразования):
Здесь: P – вероятность того, что произойдет интересующее событие; e – основание натурального логарифма (2,718); Y – стандартное уравнение множественной регрессии.
Зависимость, связывающая вероятность события и величину Y, показана на рис. 30.
Рис. 30. Логистическая (S-образная) кривая.
Существует несколько способов нахождения коэффициентов логистической регрессии. На практике чаще всего используют метод максимального правдоподобия. На самом деле, логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой – коэффициенты логистической регрессии, а вес поляризации – константа регрессионного уравнения. Подобная однослойная нейронная сеть является классическим вариантом перцептрона, который может успешно решать лишь задачу линейной сепарации, ввиду чего возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. К счастью, разбор принципов работы с нейронными сетями выходит далеко за рамки настоящего руководства. Для оценки качества модели логистической регрессии существует эффективный инструмент – упоминавшийся выше ROC-анализ. ROC-кривая (Receiver Operator Characteristic) – кривая, которая наиболее часто используется для представления результатов бинарной классификации. Название ее заимствовано из терминологии машинных систем обработки сигналов (также известна как кривая ошибок). ROC-анализ оперирует двумя классами событий – с положительными исходами и с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных исходов от количества неверно классифицированных отрицательных исходов. В терминологии ROC-анализа первые называются истинно положительным множеством, вторые – ложно отрицательным множеством. При этом предполагается, что у классификатора (исследуемой независимой переменной) имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение значений Р на два вышеупомянутых класса. Этот параметр называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода. Для понимания сути ошибок I и II рода рассмотрим неоднократно упоминавшуюся ранее четырехпольную таблицу сопряженности (confusion matrix), или таблицу 2×2, которая строится на основе результатов классификации с использованием регрессионной модели и фактической (объективной) принадлежностью наблюдений к двум вышеописанным классам:
Здесь: TP (True Positives) – верно классифицированные положительные случаи (т.н. истинно положительные случаи); TN (True Negatives) – верно классифицированные отрицательные случаи (т.н. истинно отрицательные случаи); FN (False Negatives) – положительные случаи, классифицированные как отрицательные (ошибка I рода). Это т.н. «ложный пропуск» – интересующее нас событие имеет место, но ошибочно не обнаруживается (т.н. ложноотрицательные случаи); FP (False Positives) – отрицательные случаи, классифицированные как положительные (ошибка II рода); Это т.н. «ложное обнаружение» – при фактическом отсутствии изучаемого события ошибочно принимается решение о его наличии (ложноположительные случаи).
Что именно является положительным событием, а что – отрицательным, зависит от стоящей перед учеными конкретной задачи. Например, если прогнозируется вероятность наличия заболевания, то положительным исходом будет класс «больной», а отрицательным – «здоровый». Наоборот, если необходимо оценить вероятность того, что человек здоров, то положительным исходом будет класс «здоровый», а отрицательным – «больной». При анализе чаще оперируют не абсолютными показателями, а относительными – долями (rates), выраженными в процентах. Так, доля истинно положительных случаев (True Positives Rate, TPR) вычисляется как отношение количества верно классифицированных положительных случаев к фактическому количеству положительных случаев:
Доля истинно положительных случаев (TPR) называется также «чувствительность модели», или просто «чувствительность» (sensitivity, или Se).
Соответственно, доля ложноположительных случаев (False Positives Rate, FPR) вычисляется как отношение количества неверно классифицированных отрицательных случаев к фактическому количеству отрицательных случаев:
Доля истинно отрицательных случаев (True Negative Rate, TNR) вычисляется как отношение количества верно классифицированных отрицательных случаев к фактическому количеству отрицательных случаев:
Доля истинно отрицательных случаев (TNR) называется также «специфичность модели», или просто «специфичность» (specificity, или Sp). Заметим, что FPR=100–Sp.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (хорошо обнаруживает положительные случаи). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (хорошо обнаруживает отрицательные случаи). Если рассуждать в рамках решения задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее: – чувствительный диагностический тест обусловливает гипердиагностику ввиду большой вероятности ложноположительных ответов; – специфичный диагностический тест страдает гиподиагностикой ввиду большой вероятности ложноотрицательных ответов. Обе разновидности тестов полезны при определенных ситуациях. Так, скрининговые тесты, предназначенные для массовых обследований, должны быть высокочувствительными и «широко грести» – все потенциально больные должны быть выявлены, и гипердиагностика в данном случае допустима ввиду предварительного характера указанных тестов. Ложноположительные ответы исключаются на следующем этапе обследования путем применения специальных «подтверждающих» (конфирматорных) тестов, которые, в свою очередь, должны обладать высокой специфичностью, чтобы обеспечить надежное выявление истинно больных. Подобная схема обследования, когда вначале применяется скрининговый тест с высокой чувствительностью, а при его положительном результате – конфирматорный с высокой специфичностью, широко распространена в диагностике инфекционных заболеваний.
ROC-кривая строится следующим образом: 1. Для каждого значения порога отсечения от 0 до 1 с известным шагом dx (например, 0,01) рассчитываются значения чувствительности Se и специфичности Sp. При альтернативном подходе значение dx не вводится, в качестве аргумента логистической функции последовательно используются все неповторяющиеся значения исследуемого признака в вариационном ряду, а полученные значения функции подставляются в качестве порога отсечения; 2. Строится график зависимости, где по оси Y откладывается чувствительность Se, а по оси X – доля ложноположительных случаев (FPR), т.е. 100–Sp (%). В результате получается некоторая кривая, косвенно отражающая зависимость чувствительности диагностического теста от его специфичности (см. рис. 31).
При использовании компьютерных программ (например, MedCalc) для выполнения ROC-анализа необходима специальная переменная – т.н. классификатор, которая позволяет программе отличать отрицательные случаи от положительных и, соответственно, содержит перечень закодированных исходов (0 – отрицательных, 1 – положительных), который ставится в попарное соответствие известным значениям некоторого изучаемого параметра, который и оценивается в рамках внедряемого нового метода диагностики. Ввиду этого, для успешного выполнения ROC-анализа необходим метод диагностики, используемый как эталонный и позволяющий установить фактическое количество положительных и отрицательных исходов, в противном случае анализ теряет смысл. Но, как будет показано далее, ни один метод диагностики не может иметь чувствительность и специфичность, равные 100%, ввиду чего, проводя ROC-анализ, мы фактически сравниваем предлагаемый нами новый метод диагностики не с реальным положением дел, а с другим методом, использованным в качестве эталонного, и это ограничение нельзя преодолеть.
Рис. 31. ROC-кривая типичного вида. Такой график часто дополняют прямой y=x, проходящей по диагонали из левого нижнего угла в верхний правый.
График ROC-кривой идеального классификатора проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложноположительных случаев равна нулю. Ввиду этого, чем ближе ROC-кривая подходит к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой (у=х), тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов. При визуальной оценке ROC-кривых расположение их друг относительно друга указывает на сравнительную эффективность соответствующих методов диагностики: кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис. 32 две ROC-кривые совмещены на одном графике, причем отчетливо видно, что способ диагностики A лучше, чем способ В. Визуальное сравнение ROC-кривых не всегда позволяет выявить наиболее эффективную модель. Более строгим методом сравнения является оценка площадей под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку ROC-кривые всегда расположены выше диагонали, то обычно говорят об изменениях площади под кривой от 0,5 («бесполезный классификатор») до 1,0 («идеальная модель»). Численный показатель площади под кривой называется AUC (Area Under Curve), см. рис. 33. Вычислить его можно, например, с помощью метода трапеций. С большими допущениями можно считать, что чем больше показатель AUC, тем лучшей прогностической силой обладает модель. Однако следует знать, что: – показатель AUC предназначен только для сравнительного анализа нескольких моделей (диагностических тестов); – AUC не содержит никакой информации о чувствительности и специфичности модели (исследуемого диагностического теста).
Рис. 32. Сравнение ROC-кривых.
Рис. 33. Площадь под ROC-кривой.
В литературе иногда приводится следующая экспертная шкала для значений AUC, по которой можно судить о качестве модели:
Для показателей AUC можно вычислить доверительные интервалы (обычно – 95%), сравнение которых позволяет строго установить статистическую значимость различий ROC-кривых (в том случае, если доверительные интервалы этих кривых не пересекаются).
Идеальный диагностический тест обладает 100% чувствительностью и такой же специфичностью. Однако на практике добиться этого невозможно; более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью т.н. порога отсечения, т.к. его величина влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value). Порог отсечения нужен для того, чтобы применять диагностический тест на практике – относить новые случаи к одному из двух классов. Проще говоря, порог отсечения – это та величина измеряемого диагностическим тестом параметра, по достижении которой принимается решение о наличии патологического состояния. Для определения оптимального порога отсечения нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать: – требование максимальной величины чувствительности либо специфичности теста. Например, нужно обеспечить чувствительность методики не менее 80%. В этом случае порог отсечения должен соответствовать максимальной специфичности, достижимой при величине чувствительности ≈80% (таких значений может быть несколько из-за дискретности ряд); – требование максимальной суммарной чувствительности и специфичности модели; – требование баланса между чувствительностью и специфичностью, т.е. когда чувствительность ≈ специфичности. В данном случае величина порога отсечения определяется как точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y –чувствительность и специфичность модели (рис. 34). При этом следует учитывать, что при повышении чувствительности неизбежно падает специфичность, и наоборот – это вытекает из самой сущности ROC-анализа. Уменьшение величины порога отсечения повышает чувствительность, увеличение – специфичность.
Рис. 34. Нахождение «точки баланса» между чувствительностью и специфичностью.
Таким образом, ROC-анализ позволяет: 1. Определить величину порога отсечения теста применительно к конкретной диагностической задаче (см. выше перечень возможных задач); 2. Рассчитать чувствительность и специфичность диагностического теста, соответствующие найденному значению порога отсечения; 3. Построить ROC-кривую, определить для нее AUC и его 95% ДИ; 4. Сравнить несколько диагностических тестов при помощи сравнения величин AUC их ROC-кривых, показать статистическую значимость различий путем сравнения ДИ.
Соответственно, при оформлении научной публикации для каждого предлагаемого диагностического теста необходимо указывать: – величину порога отсечения, установленную для решаемой диагностической задачи; – соответствующие этой величине чувствительность и специфичность; – AUC и его 95% доверительный интервал; – величину р (показатель вероятности нулевой гипотезы), которая должна быть равна или меньше оговоренного уровня значимости (α); обычно α≤0,05. Помимо перечисленных характеристик, для каждого диагностического теста можно рассчитать ряд дополнительных показателей, характеризующих его практическую ценность:
Предсказательная значимость положительного теста (ПЗПТ) – вычисляется как процентное отношение количества истинно положительных результатов к общему числу положительных результатов, полученных при использовании диагностического теста:
Предсказательная значимость отрицательного теста (ПЗОТ) – вычисляется как процентное отношение количества истинно отрицательных результатов к общему числу отрицательных результатов, полученных при использовании диагностического теста:
Диагностическая эффективность (значимость) теста (ДЭТ) – вычисляется как процентное отношение количества истинных результатов диагностического теста к общему числу полученных результатов:
Заключение
Описанные в данной главе методы статистического анализа являются минимально достаточными для осуществления статистической обработки результатов правильно спланированного и должным образом выполненного исследования биомедицинской направленности. В настоящем руководстве будут описаны и более сложные статистические приемы применительно к специальным типам научного дизайна – когортным исследованиям, рандомизированным клиническим испытаниям и мета-анализу (см. Главу III). Ряд вопросов, непосредственно касающихся приемов работы с интерфейсом программ для статистического анализа, специально не рассматривался, поскольку даже автор настоящей главы, не будучи профессиональным статистиком, использует в своей повседневной практике ЧЕТЫРЕ таких программы. Более того, постоянно выходят их обновленные версии, так что любое описание пошаговых приемов работы с актуальными версиями таких программ обречено на скорое и неминуемое устаревание. Автор считает, что подобные вопросы должны разбираться на семинарских занятиях, и желает читателям успехов на исследовательском поприще, равно как и в деле освоения современных приемов статистической обработки научных данных.
|