Г. Математическое приложениеОпределение монопольной цены можно показать и аналитически. Монополист хочет максимизировать свою прибыль, которая есть разница между его выручкой и совокупными затратами. Как выручка, так и затраты монополии – функции ее выпуска: TR=TR(q)=P(q)*q и TC=TC(q). Поэтому функцию прибыли можно записать так: П=TR-TC=P(q)*q-TC(q)®max. Необходимо определить выпуск, при котором прибыль максимальна. Для этого берем производную функции прибыли по выпуску и приравниваем результат к нулю:
Левая часть последнего уравнения представляет собой предельный доход монополии (см. п. 2А настоящей темы), а правая – ее предельные затраты. Тем самым строго доказано, что максимизирующий прибыль выпуск соответствует точке, в которой MR=MC. Продолжаем преобразования:
Вспомним формулу эластичности спроса по цене:
Выводы: а) поскольку эластичность спроса по цене отрицательна, монопольная цена превышает предельные затраты (что было показано графически); б) монополист устанавливает цену на эластичном участке кривой спроса;[2] в) чем эластичнее спрос по цене, тем меньше разница между ценой и предельными затратами. Последнее можно обосновать логически. Высокая эластичность спроса по цене говорит о том, что данный товар достаточно легко заменить. Поэтому монополия в состоянии лишь незначительно повысить цену в сравнении с предельными затратами: при повышении цены покупатели в массовом порядке переключаются на товары-заменители. Продолжим преобразования:
Выражение
|
. Отсюда: 
. Следовательно: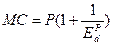 
. Отсюда: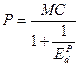
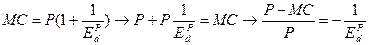
– это коэффициент Лернера, показывающий относительное превышение цены над предельными затратами и характеризующий, тем самым, рыночную власть монополиста. Как видно из последней формулы, коэффициент Лернера оказывается тем ниже, чем эластичнее спрос по цене. При бесконечно эластичном спросе (кривая спроса горизонтальна) он равен нулю, т.е. цена совпадает с предельными затратами, что является признаком совершенной конкуренции.
