График дифференцируемой функции  называется выпуклым вниз на интервале
называется выпуклым вниз на интервале  , если он расположен выше
, если он расположен выше  её касательной на этом интервале. График функции
её касательной на этом интервале. График функции  называется выпуклым вверх на интервале
называется выпуклым вверх на интервале  , если он расположен ниже
, если он расположен ниже  её касательной на этом интервале.
её касательной на этом интервале.
Точка графика непрерывной функции  , отделяющая его части разной выпуклости, называется точкой перегиба.
, отделяющая его части разной выпуклости, называется точкой перегиба.
 Кривая
Кривая  выпукла вверх в интервале
выпукла вверх в интервале 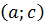 , выпукла вниз в интервале
, выпукла вниз в интервале  , точка
, точка  – точка перегиба.
– точка перегиба.
Теорема 9. Если функция  во всех точках интервала
во всех точках интервала  имеет отрицательную вторую производную, т.е.
имеет отрицательную вторую производную, т.е.  , то график функции в этом интервале выпуклый вверх. Если же
, то график функции в этом интервале выпуклый вверх. Если же 
 – график выпуклый вниз.
– график выпуклый вниз.
Для нахождения точек перегиба графика функции используется следующая теорема.
Теорема 10. (достаточное условие существования точек перегиба). Если вторая производная  при переходе через точку
при переходе через точку  , в которой она = 0 или
, в которой она = 0 или  , меняет знак, то точка графика с абсциссой
, меняет знак, то точка графика с абсциссой  есть точка перегиба.
есть точка перегиба.
Пример. Исследовать на выпуклость и точки перегиба график функции  .
.
Находим, что  ,
,  . 2 –ая производная
. 2 –ая производная 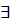 на всей числовой оси:
на всей числовой оси:  при
при  .
.
 при
при  ;
;  при
при  .
.
 график функции
график функции  в интервале
в интервале  – выпуклый вверх, в интервале
– выпуклый вверх, в интервале  – выпуклый вниз. Точка
– выпуклый вниз. Точка  есть точка перегиба.
есть точка перегиба.
Асимптоты графика функции.
 Построение графика функции значительно облегчается, если знать его асимптоты.
Построение графика функции значительно облегчается, если знать его асимптоты.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремиться к 0 при неограниченном удалении от начала координат этой точки по кривой.
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Говорят, что прямая  является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , если
, если  , или
, или  , или
, или  .
.
 Действительно, в этом случае непосредственно из рисунка видно, что расстояние точки
Действительно, в этом случае непосредственно из рисунка видно, что расстояние точки  кривой от прямой
кривой от прямой  равно
равно  . Если
. Если  , то
, то  . Согласно определению асимптоты, прямая
. Согласно определению асимптоты, прямая  является асимптотой кривой
является асимптотой кривой  .
.
Для отыскания вертикальных асимптот нужно найти те значения  , вблизи которых функция
, вблизи которых функция  неограниченно возрастает по модулю. Обычно это точки разрыва 2 –го рода.
неограниченно возрастает по модулю. Обычно это точки разрыва 2 –го рода.
Например, кривая  имеет вертикальную асимптоту
имеет вертикальную асимптоту  , так как
, так как  ,
,  .
.
Уравнение наклонной асимптоты будем искать в виде
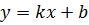 .
.
Найдём  и
и  .
.
 .
.
 .
.
Итак, если 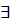 наклонная асимптота
наклонная асимптота  , то
, то  и
и  находятся по приведённым выше формулам.
находятся по приведённым выше формулам.
Верно и обратное утверждение: если 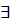 конечные пределы
конечные пределы  и
и  , то прямая
, то прямая 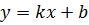 является наклонной асимптотой.
является наклонной асимптотой.
Если хотя бы один из пределов или  , или
, или 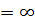 , то кривая
, то кривая  наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
В частности, если 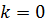 , то
, то  . Поэтому
. Поэтому  – уравнение горизонтальной асимптоты.
– уравнение горизонтальной асимптоты.
Замечание: Асимптоты графика функции  при
при  и
и  могут быть разными. Поэтому при нахождении пределов
могут быть разными. Поэтому при нахождении пределов  и
и  следует отдельно рассматривать случай, когда
следует отдельно рассматривать случай, когда  и когда
и когда  .
.
Пример. Найти асимптоты графика функции 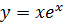 .
.
Так как  , то график функции при
, то график функции при  наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
При  справедливы соотношения
справедливы соотношения
 ,
,
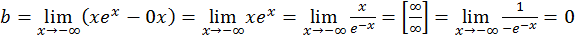 .
.
 при
при  график имеет горизонтальную асимптоту
график имеет горизонтальную асимптоту 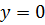 .
.
Общая схема исследования функции и построение графика.
Исследование функции  целесообразно вести в определённой последовательности.
целесообразно вести в определённой последовательности.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями координат.
3. Найти интервалы знакопостоянства функции (промежутки, на которых  или
или  ).
).
4. Выяснить, является ли функция чётной, нечётной или общего вида.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности функции.
7. Найти экстремумы функции.
8. Найти интервалы выпуклости и точки перегиба функции.
На основании проведенного исследования построить график функции. В более простых случаях достаточно выполнить лишь несколько операций, например 1, 2, 7. Если же график функции не совсем понятен и после выполнения всех 8 операций, то можно дополнительно исследовать функцию на периодичность, построить дополнительно несколько точек графика, выявить другие особенности функции. Иногда целесообразно выполнение операций исследования сопровождать постепенным построением графика функции.
Пример. Исследовать функцию  и построить её график.
и построить её график.
Выполним все 8 операций схемы исследования.
1. Функция не определена при  и
и  . Область её определения состоит из 3 интервалов
. Область её определения состоит из 3 интервалов 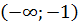 ,
,  ,
,  , а график из 3 ветвей.
, а график из 3 ветвей.
2. Если  , то
, то 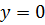 . График пересекает ось
. График пересекает ось  в точке
в точке  ; если
; если 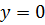 , то
, то  . График пересекает ось
. График пересекает ось  в точке
в точке  .
.
3. Функция знакоположительна (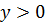 ) в интервалах
) в интервалах 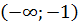 и
и  ; знакоотрицательна – в
; знакоотрицательна – в  и
и  .
.
4. Функция является  нечетной, т.к.
нечетной, т.к.
 .
.
 график её симметричен относительно начала координат.
график её симметричен относительно начала координат.
Для построения графика достаточно исследовать её при  .
.
5. Прямые  и
и  являются её вертикальными асимптотами.
являются её вертикальными асимптотами.
Выясним наличие наклонной асимптоты:
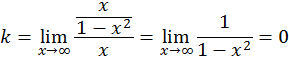
(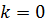 при
при  и при
и при  ),
),
 .
.
 есть горизонтальная асимптота, её уравнение
есть горизонтальная асимптота, её уравнение 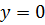 . Прямая
. Прямая 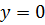 является асимптотой и при
является асимптотой и при  , и при
, и при  .
.
6. Находим интервалы возрастания и убывания функции. Так как
 ,
,
то 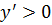 в области определения, и функция является возрастающей на каждом интервале области определения.
в области определения, и функция является возрастающей на каждом интервале области определения.
7. Исследуем функцию на экстремум. Так как  , то критическими точками являются точки
, то критическими точками являются точки  и
и 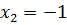 (
( не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
8. Исследуем функцию на выпуклость. Находим  :
:
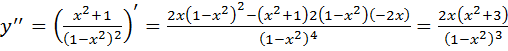 .
.
Вторая производная  или не существует в точках
или не существует в точках  ,
, 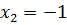 ,
,  .
.
 На рисунке представлена схема изменения знаков 2 – ой производной исследуемой функции.
На рисунке представлена схема изменения знаков 2 – ой производной исследуемой функции.
 Точка
Точка  – точка перегиба графика функции.
– точка перегиба графика функции.
График выпуклый вверх на интервалах  и
и  ; выпуклый вниз на интервалах
; выпуклый вниз на интервалах  и
и  .
.

 называется выпуклым вниз на интервале
называется выпуклым вниз на интервале  , если он расположен выше
, если он расположен выше  её касательной на этом интервале. График функции
её касательной на этом интервале. График функции  Кривая
Кривая 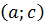 , выпукла вниз в интервале
, выпукла вниз в интервале  , точка
, точка  – точка перегиба.
– точка перегиба. , то график функции в этом интервале выпуклый вверх. Если же
, то график функции в этом интервале выпуклый вверх. Если же 
 – график выпуклый вниз.
– график выпуклый вниз. при переходе через точку
при переходе через точку  , в которой она = 0 или
, в которой она = 0 или  , меняет знак, то точка графика с абсциссой
, меняет знак, то точка графика с абсциссой  .
. ,
,  . 2 –ая производная
. 2 –ая производная 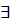 на всей числовой оси:
на всей числовой оси:  при
при  .
. при
при  ;
;  при
при  .
. график функции
график функции  – выпуклый вверх, в интервале
– выпуклый вверх, в интервале  – выпуклый вниз. Точка
– выпуклый вниз. Точка  есть точка перегиба.
есть точка перегиба. Построение графика функции значительно облегчается, если знать его асимптоты.
Построение графика функции значительно облегчается, если знать его асимптоты. является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , или
, или  , или
, или  .
. Действительно, в этом случае непосредственно из рисунка видно, что расстояние точки
Действительно, в этом случае непосредственно из рисунка видно, что расстояние точки  кривой от прямой
кривой от прямой  . Если
. Если  , то
, то  . Согласно определению асимптоты, прямая
. Согласно определению асимптоты, прямая  , вблизи которых функция
, вблизи которых функция  неограниченно возрастает по модулю. Обычно это точки разрыва 2 –го рода.
неограниченно возрастает по модулю. Обычно это точки разрыва 2 –го рода. имеет вертикальную асимптоту
имеет вертикальную асимптоту  , так как
, так как  ,
,  .
.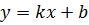 .
. и
и  .
. .
. .
. , то
, то  и
и 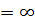 , то кривая
, то кривая 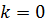 , то
, то  . Поэтому
. Поэтому  – уравнение горизонтальной асимптоты.
– уравнение горизонтальной асимптоты. и
и  могут быть разными. Поэтому при нахождении пределов
могут быть разными. Поэтому при нахождении пределов 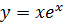 .
. , то график функции при
, то график функции при  ,
,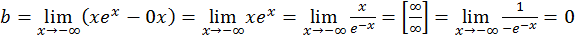 .
. .
. или
или  ).
). и построить её график.
и построить её график. и
и 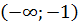 ,
,  ,
,  , а график из 3 ветвей.
, а график из 3 ветвей. в точке
в точке  ; если
; если  в точке
в точке  .
.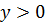 ) в интервалах
) в интервалах  ; знакоотрицательна – в
; знакоотрицательна – в  и
и  .
. .
.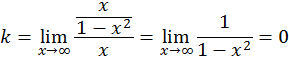
 .
. ,
,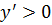 в области определения, и функция является возрастающей на каждом интервале области определения.
в области определения, и функция является возрастающей на каждом интервале области определения. , то критическими точками являются точки
, то критическими точками являются точки  и
и 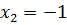 (
( не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет. :
: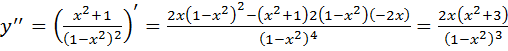 .
. или не существует в точках
или не существует в точках  ,
,  .
. На рисунке представлена схема изменения знаков 2 – ой производной исследуемой функции.
На рисунке представлена схема изменения знаков 2 – ой производной исследуемой функции. Точка
Точка  ; выпуклый вниз на интервалах
; выпуклый вниз на интервалах  и
и 


